1. Graph의 정의

---

• 그래프는 여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조이다.

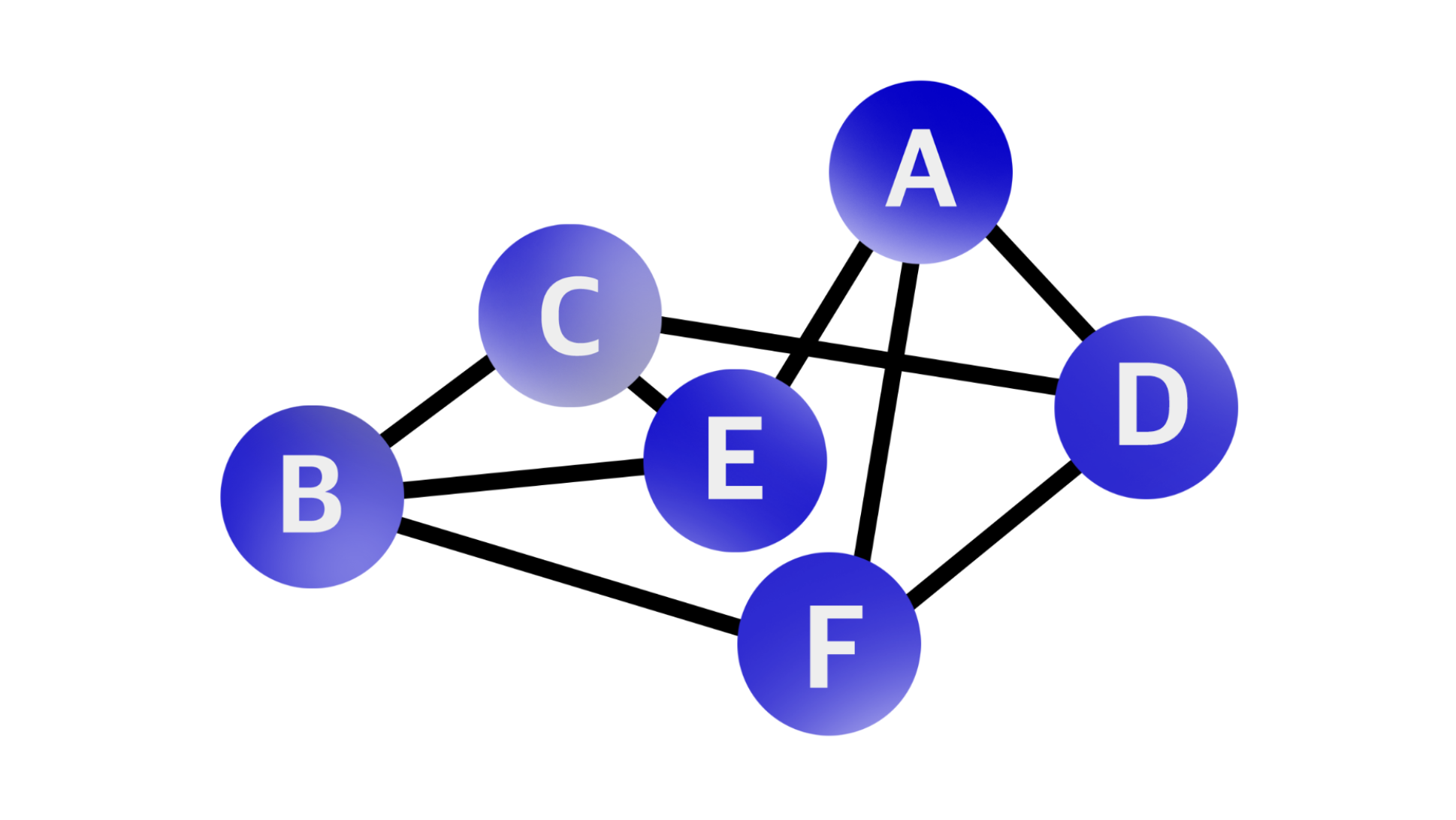
2. Graph의 구조

---

• 직접적인 관계가 있는 경우 두 점 사이를 이어주는 선이 있다.

• 간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어진다.

• 하나의 점을 그래프에서는 정점(vertex)이라고 표현하고, 하나의 선은 간선(edge)이라고 한다.

3. Graph의 표현 방식

---

1) 인접 행렬

• 두 정점을 바로 이어주는 간선이 있다면 이 두 정점은 인접하다고 표현한다. 인접 행렬은 서로 다른 정점들이 인접한 상태인지를 표시한 행렬로 2차원 배열의 형태로 나타냅니다.

• 만약 A라는 정점과 B라는 정점이 이어져 있다면 1(true), 이어져 있지 않다면 0(false)으로 표시한 일종의 표다. 만약 가중치 그래프라면 1 대신 관계에서 의미 있는 값을 저장한다. 내비게이션 그래프를 인접 행렬로 표현하면 아래와 같다.

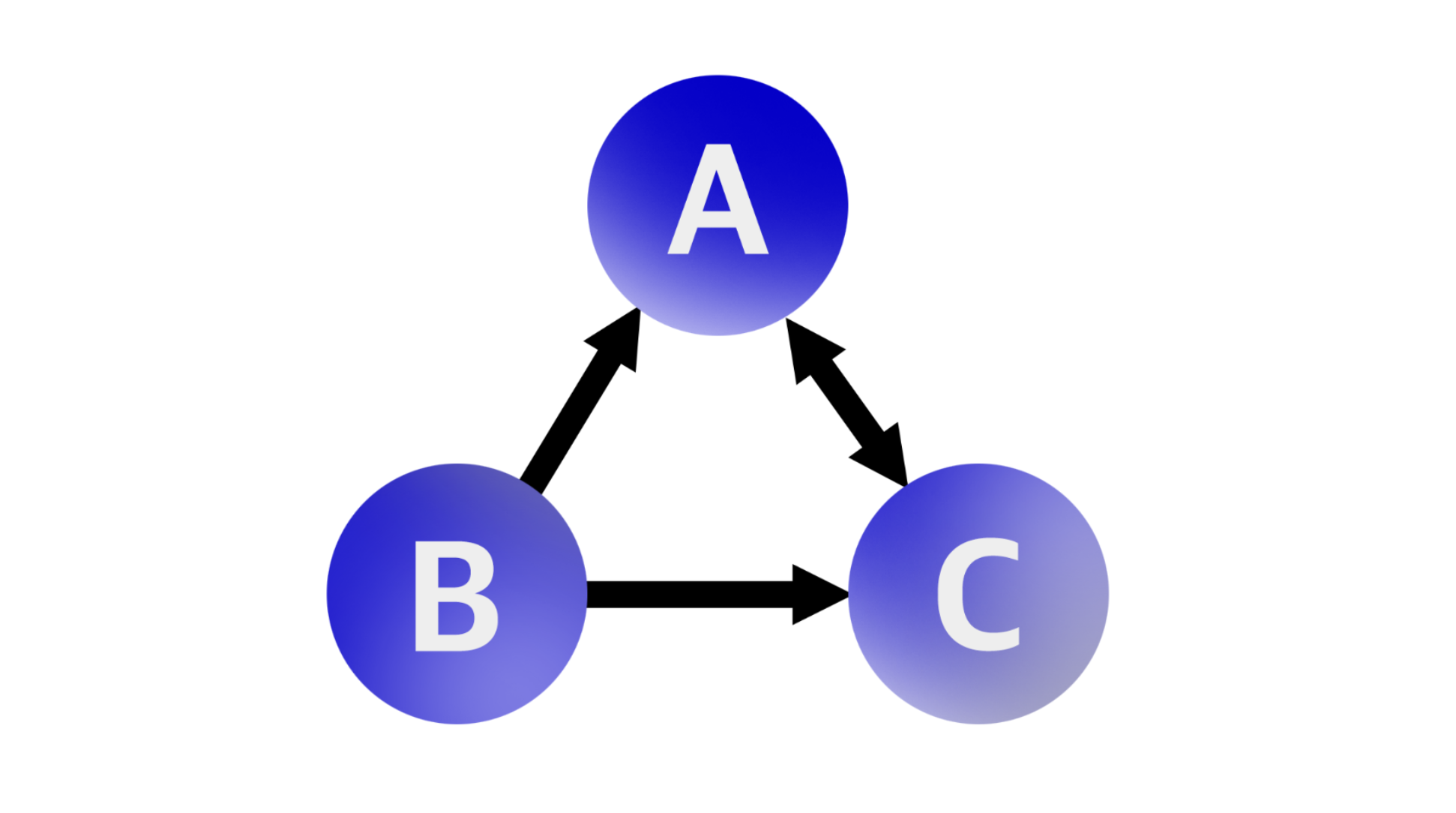
• A의 진출차수는 1개 입니다: A —> C
  [0][2] === 1

• B의 진출차수는 2개 입니다: B —> A, B —> C
  [1][0] === 1
  [1][2] === 1

• C의 진출차수는 1개입니다: C —> A
  [2][0] === 1

• 인접 행렬은 한 개의 큰 표와 같은 모습을 한 인접 행렬은 두 정점 사이에 관계가 있는지, 없는지 확인하기에 용이하다.

• 예를 들어, A에서 B로 진출하는 간선이 있는지 파악하기 위해선 0 번째 줄의 1 번째 열에 어떤 값이 저장되어있는지 바로 확인할 수 있다.

• 인접 행렬은 가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용된다.

2) 인접 리스트

• 인접 리스트는 각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 표현한다. 각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있다. 위 그래프를 인접 리스트로 표현하면 아래와 같다.

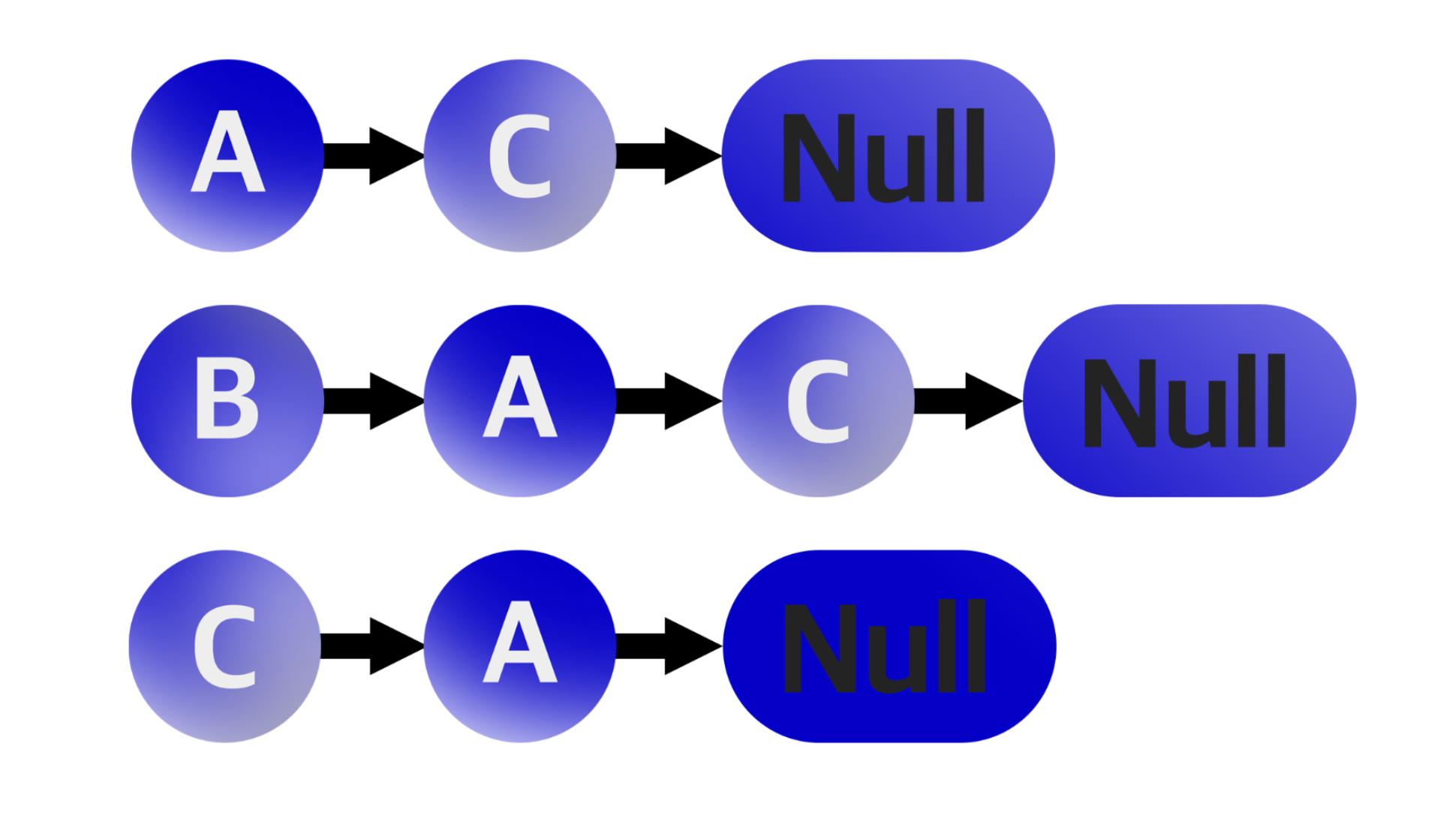
B는 A와 C로 이어지는 간선이 두 개가 있는데, A가 C보다 먼저 나오는 이유

• 여기서 B는 A와 C로 이어지는 간선이 두 개가 있는데, A가 C보다 먼저 나온다. 그러나 이 순서는 보통 중요하지 않다.

• 그래프, 트리, 스택, 큐 등 모든 자료구조는 구현하는 사람의 편의와 목적에 따라 기능을 추가/삭제할 수 있다. 그래프를 인접 리스트로 구현할 때, 정점별로 살펴봐야 할 우선 순위를 고려해 구현할 수 있다.

• 이때, 리스트에 담겨진 정점들을 우선 순위별로 정렬할 수 있다. 우선 순위가 없다면, 연결된 정점들을 단순하게 나열한 리스트가 된다.

• 우선 순위를 다뤄야 한다면 더 적합한 자료구조(ex. queue, heap)를 사용하는 것이 합리적이므로 따라서 보통은 중요하지 않다. (언제나 예외는 있습니다.)

• 인접 리스트는 메모리를 효율적으로 사용하고 싶을 때 인접 리스트를 사용한다. 인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지하기 때문이다.

4. Graph의 실사용 예제

---

• 대표적으로 내비게이션 등에서 사용하는 자료구조가 그래프이다. 수많은 정점을 가지고 있고, 서로 관계가 있는 정점은 간선으로 이어져 있다.

let isConnected = {
  seoul: {
    busan: true,
    daejeon: true
  },
  daejeon: {
    seoul: true,
    busan: true
  },
  busan: {
    seoul: true,
    daejeon: true
  }
}

console.log(isConnected.seoul.daejeon) // true
console.log(isConnected.daejeon.busan) // true

• 위 정보만으로는 서울에서 부산까지 갈 수 있다는 사실 외에 파악할 수 있는 정보가 없다. 비가중치 그래프는 각 정점 간의 연결 유무만을 판단하는 반면, 가중치 그래프는 더 자세한 정보를 담을 수 있다.

• 추가적인 정보를 파악할 수 없는 그래프, 가중치(연결의 강도가 얼마나 되는지)가 적혀 있지 않은 이런 그래프를 비가중치 그래프라고 한다.

• 정점: 서울, 대전, 부산
• 간선: 서울—140km—대전, 대전—200km—부산, 부산—325km—서울

• 이렇게 간선에 연결 강도(거리 등)를 표현한 그래프를 가중치 그래프라고 한다. 내비게이션은 간선에 거리를 표기한 가중치 그래프가 확장되어, 수백만 개의 정점(주소)과 간선이 추가되어야 비로소 내비게이션에서 쓰는 자료구조와 유사해진다.