1. 순열

---

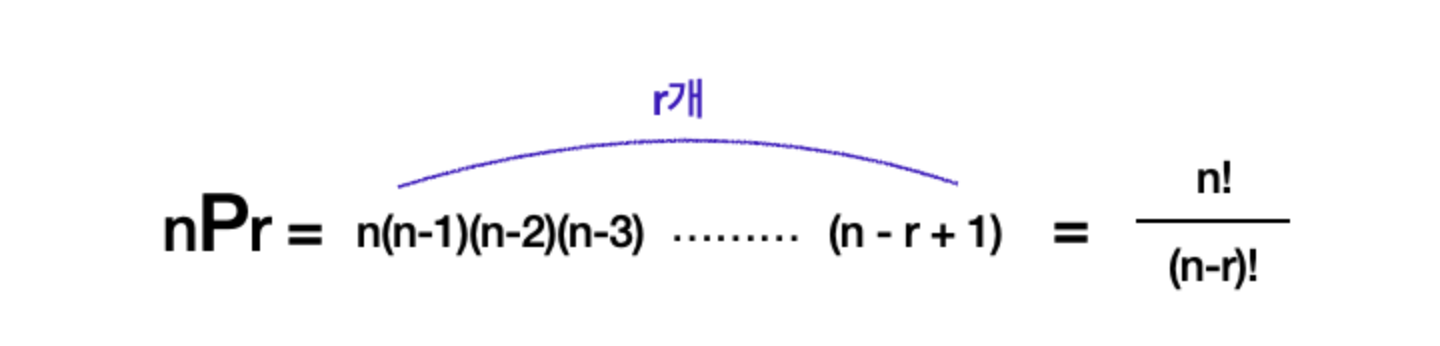
• 순열(permutation)은 서로 다른 n개의 원소를 가지는 집합에서 순서를 고려하여 중복 없이 r개의 원소로 이루어진 부분집합을 만드는 것이다.

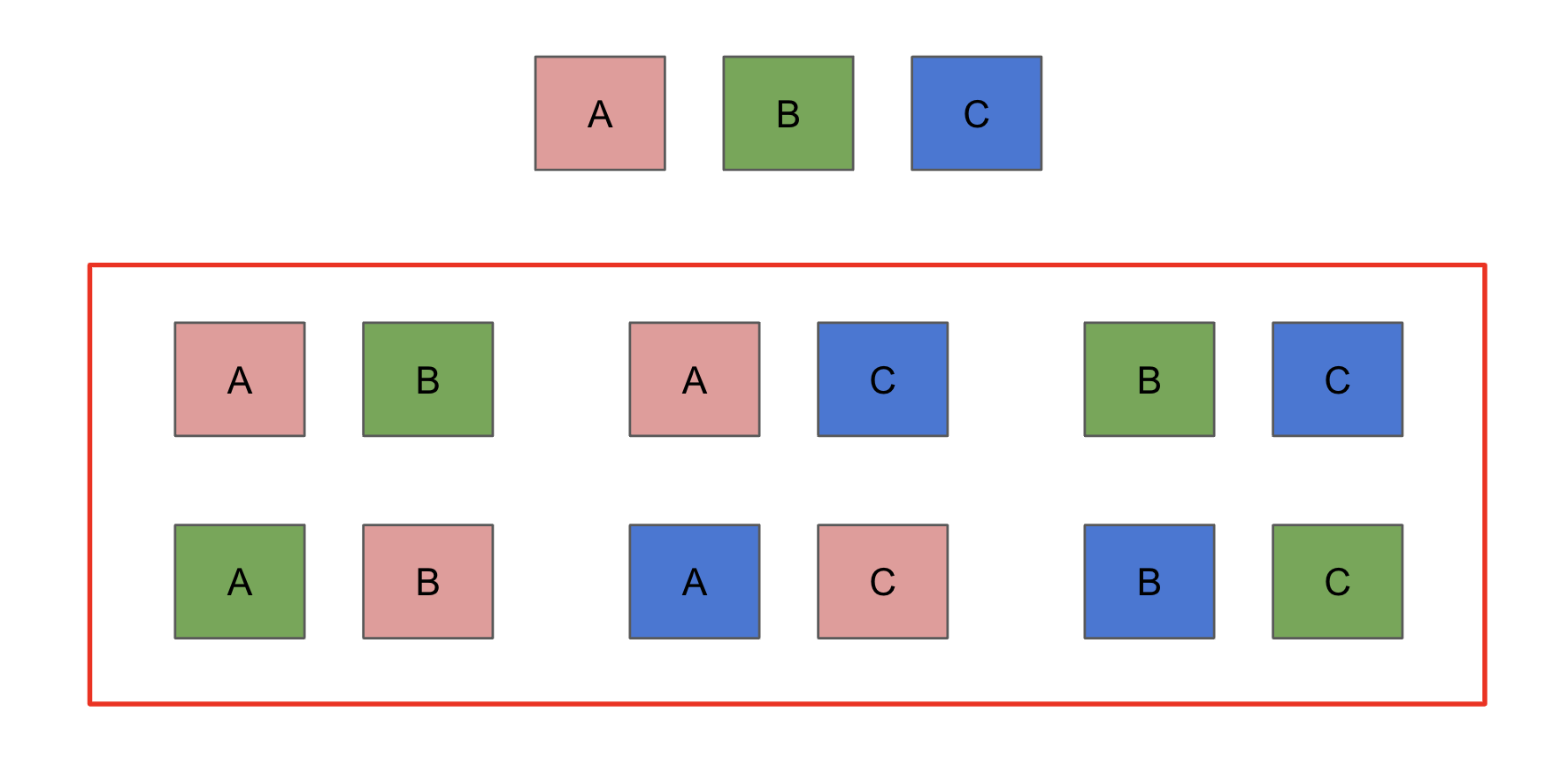
• 아래는 서로 다른 A, B, C 3개의 원소로 이루어진 집합에서 2개의 원소를 순서를 고려하여 중복 없이 부분집합을 만들면 총 6개의 부분집합이 나오게 된다.

function permutationLoop(lookup) {
    // 순열 요소가 인자로 주어질 경우, 인자 그대로 사용하면 되지만, 인자가 주어지지 않고
    // 문제 안에 포함되어 있을 경우 아래와 같이 직접 작성하여 사용한다.
    let lookup = ['A', 'B', 'C', 'D', 'E'];
    let result = [];

    for (let i = 0; i < lookup.length; i++) {
        for (let j = 0; j < lookup.length; j++) {
            for (let k = 0; k < lookup.length; k++) {
                if (i === j || j === k || k === i) continue;
                result.push([lookup[i], lookup[j], lookup[k]])
            }
        }
    }
    return result;
}

console.log(permutationLoop());

2. 조합

---

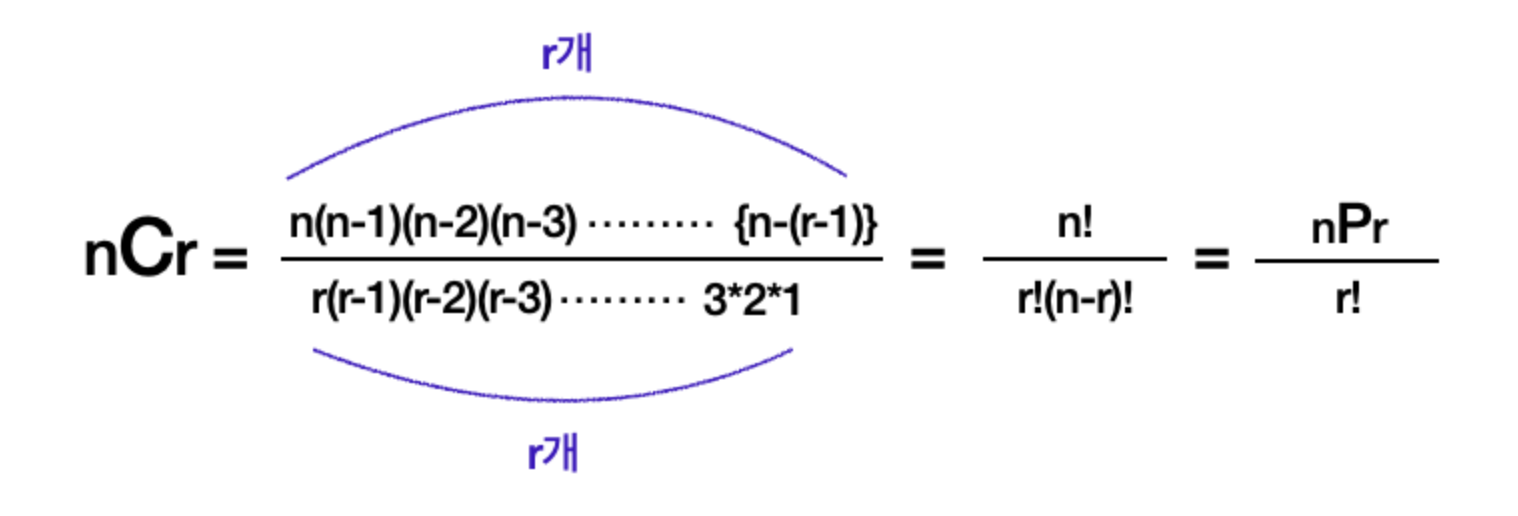
• 조합(combination)은 서로 다른 n개의 원소를 가지는 집합에서 순서를 고려하지 않고 중복 없이 r개의 원소로 이루어진 부분집합을 만드는 것이다.

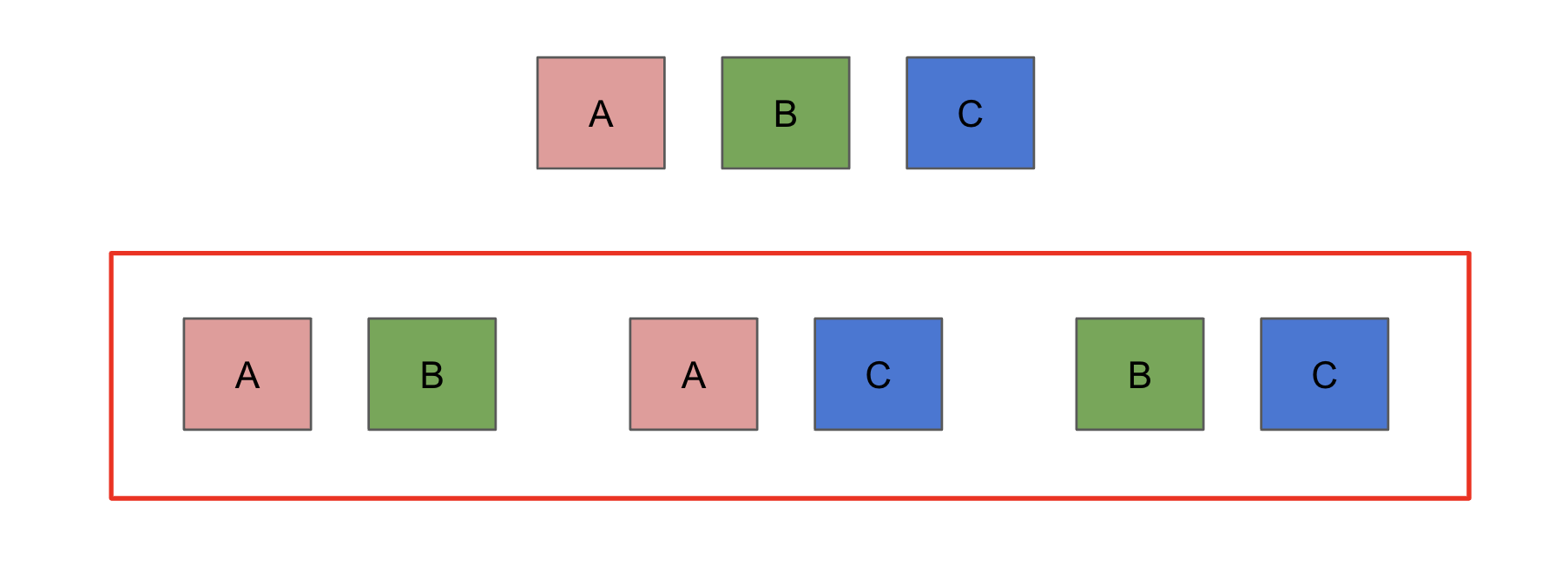
• 아래는 서로 다른 A, B, C 3개의 원소로 이루어진 집합에서 2개의 원소를 순서를 고려하지 않고 중복 없이 부분집합을 만들면 총 3개의 부분집합이 나오게 된다.

function combinationLoop() {
    // 조합 요소가 인자로 주어질 경우, 인자 그대로 사용하면 되지만, 인자가 주어지지 않고
    // 문제 안에 포함되어 있을 경우 아래와 같이 직접 작성하여 사용한다.
    let lookup = ['A', 'B', 'C', 'D', 'E'];
    let result = [];

    for (let i = 0; i < lookup.length; i++) {
        for (let j = i + 1; j < lookup.length; j++) {
            for (let k = j + 1; k < lookup.length; k++) {
                result.push([lookup[i], lookup[j], lookup[k]]);
            }
        }
    }
    return result;
}

console.log(combinationLoop());