1. 이진 탐색(Binary Search)

---

• 이진 탐색 알고리즘은 정렬되어 있는 배열에서만 사용할 수 있다.

• 배열에서 중간점을 선택하고, 찾을 값이 중간점을 기준으로 좌측에 있는지 우측에 있는지 확인한다. 분할 정복(Divide and Conquer)의 개념이다.

• 아래는 배열 arr를 입력받고, 찾을 값인 target을 입력받아 target이 몇 번째 index에 있는지를 리턴하는 함수다.

의사코드

1. 배열의 시작 인덱스와 마지막 인덱스, 그리고 그 중간 지점에 있는 중간 인덱스를 나타내는 변수를 만든다.
2. 마지막 인덱스가 시작 인덱스 보다 크거나 작을때까지
   2-1. 시작 인덱스와 마지막 인덱스가 변경될 때마다 중간 지점에 있는 중간 인덱스의 위치를 갱신한다.
   2-2. 원하는 값을 찾으면 해당 값의 인덱스를 반환한다.
   2-3. 중간 인덱스의 값보다 찾으려는 값이 크다면 시작 인덱스를 중간 인덱스 + 1의 위치로 변경한다.
   2-4. 중간 인덱스의 값보다 찾으려는 값이 작다면 마지막 인덱스를 중간 인덱스 - 1의 위치로 변경한다.
3. 2의 과정을 값을 찾을때 까지 반복한다.
4. 마지막까지 찾는 값이 배열에 없다면 -1을 반환하고 탐색을 종료한다.

const binarySearch = function (arr, target) {
  let startIndex = 0;
  let endIndex = arr.length - 1;
  let middleIndex = Math.floor((startIndex + endIndex) / 2);

  while (startIndex <= endIndex) {
    middleIndex = Math.floor((startIndex + endIndex) / 2);
    if (arr[middleIndex] === target) {
      return middleIndex;
    } else if (arr[middleIndex] < target) {
      startIndex = middleIndex + 1;
    } else {
      endIndex = middleIndex - 1;
    }
  }
  return -1;
};

1) step 1

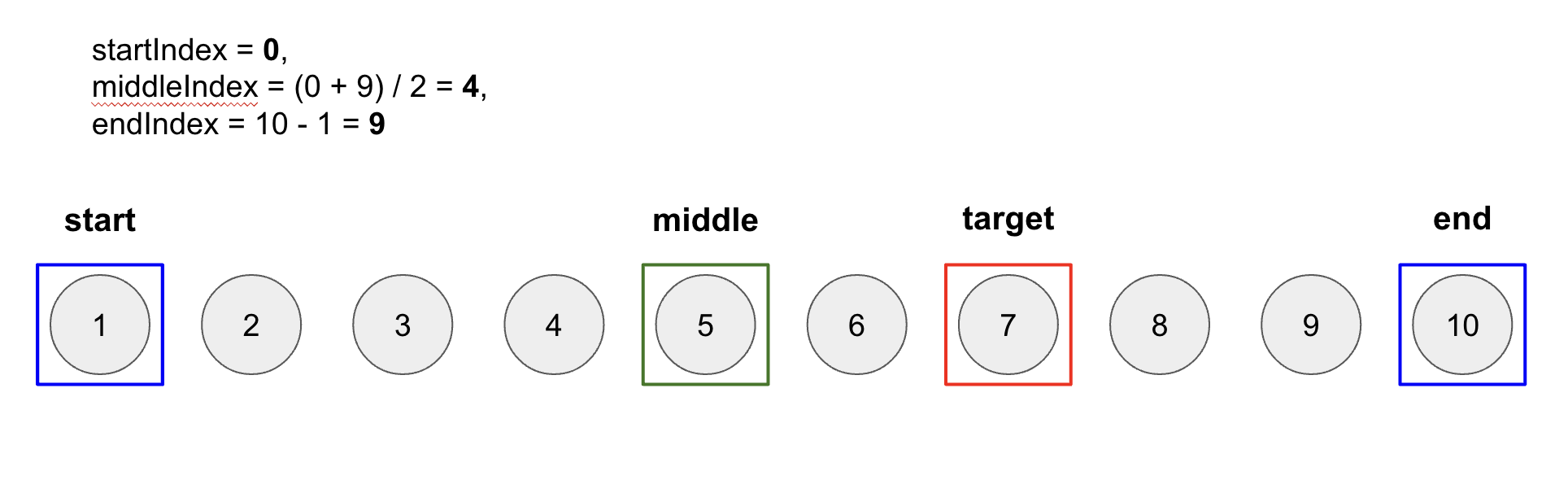
• 첫 탐색 시 target은 7이고, startIndex = 0, middleIndex = 4, endIndex = 9다.

• 현재 arr[middleIndex]의 값이 target값 보다 작으므로 arr[middleIndex] 이전의 값들은 살펴볼 필요가 없기 때문에 startIndex를 middleIndex보다 1 증가시킨 구간을 다시 탐색한다.

2) step 2

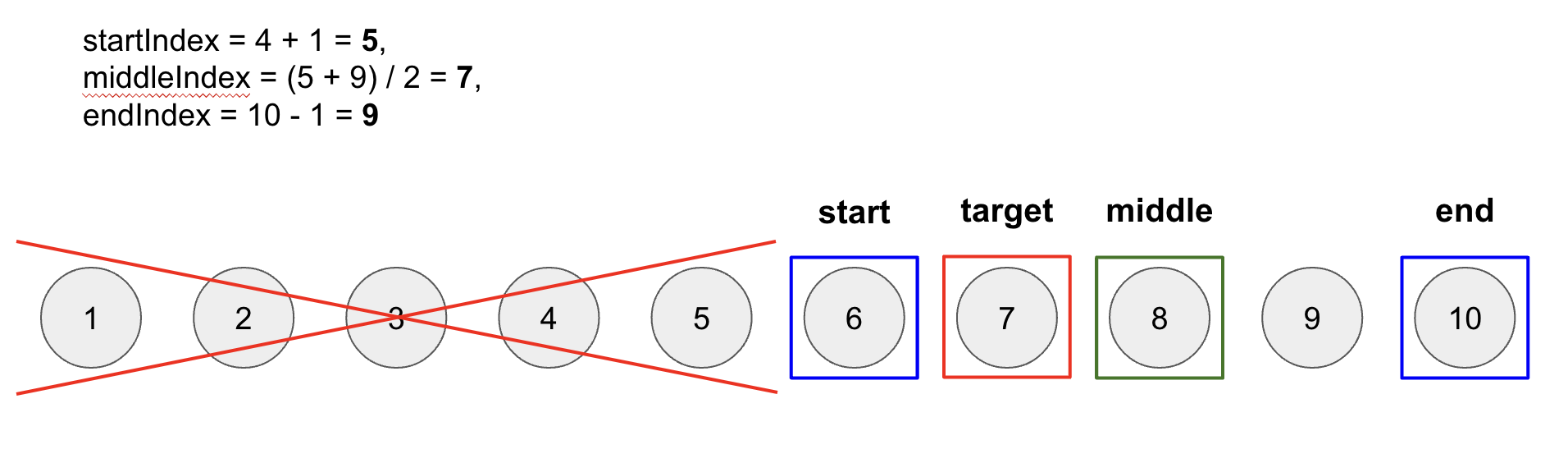
• middleIndex에 1을 더한 startIndex값은 5이고, middleIndex값은 7이 된다.

• 이번에는 arr[middleIndex]의 값이 target값 보다 크므로 arr[middleIndex] 이후의 값들은 살펴볼 필요가 없기 때문에 endIndex를 middleIndex보다 1 감소시킨 구간을 다시 탐색한다.

3) step 3

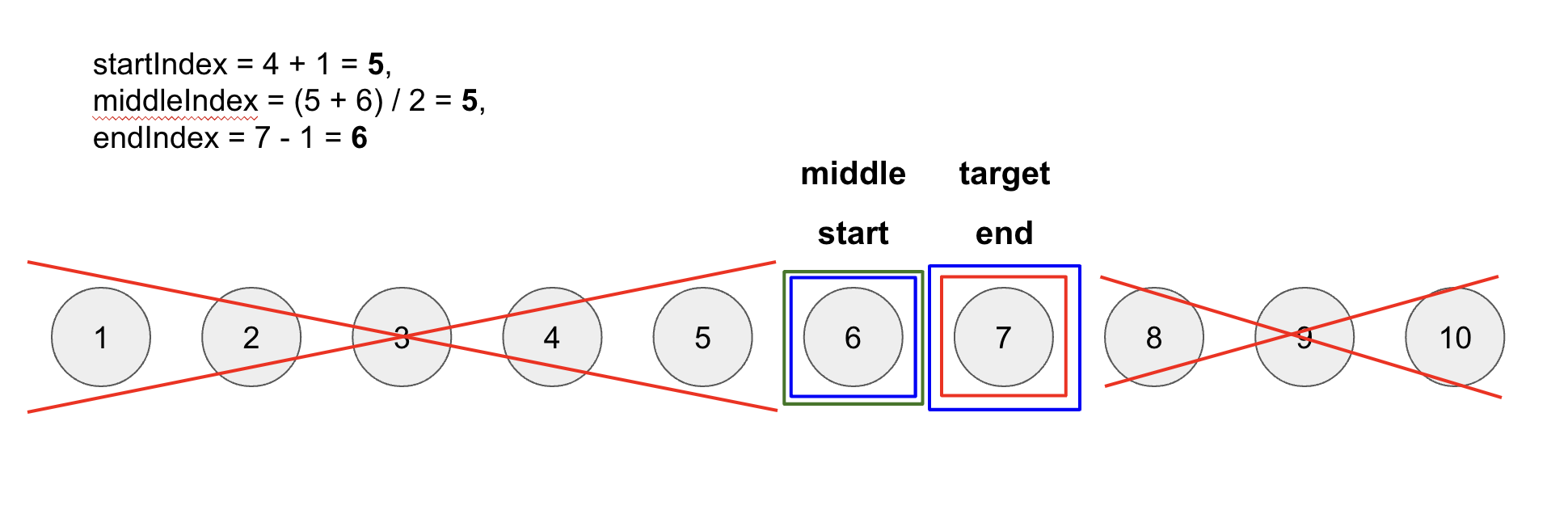
• middleIndex에 1을 뺀 endIndex값은 6이고, middleIndex값은 5가 된다.

• 이번에는 arr[middleIndex]의 값이 target 값 보다 작으므로 arr[middleIndex] 이전의 값들은 살펴볼 필요가 없기 때문에 startIndex를 middleIndex보다 1 증가시킨 구간을 다시 탐색한다.

4) step 4

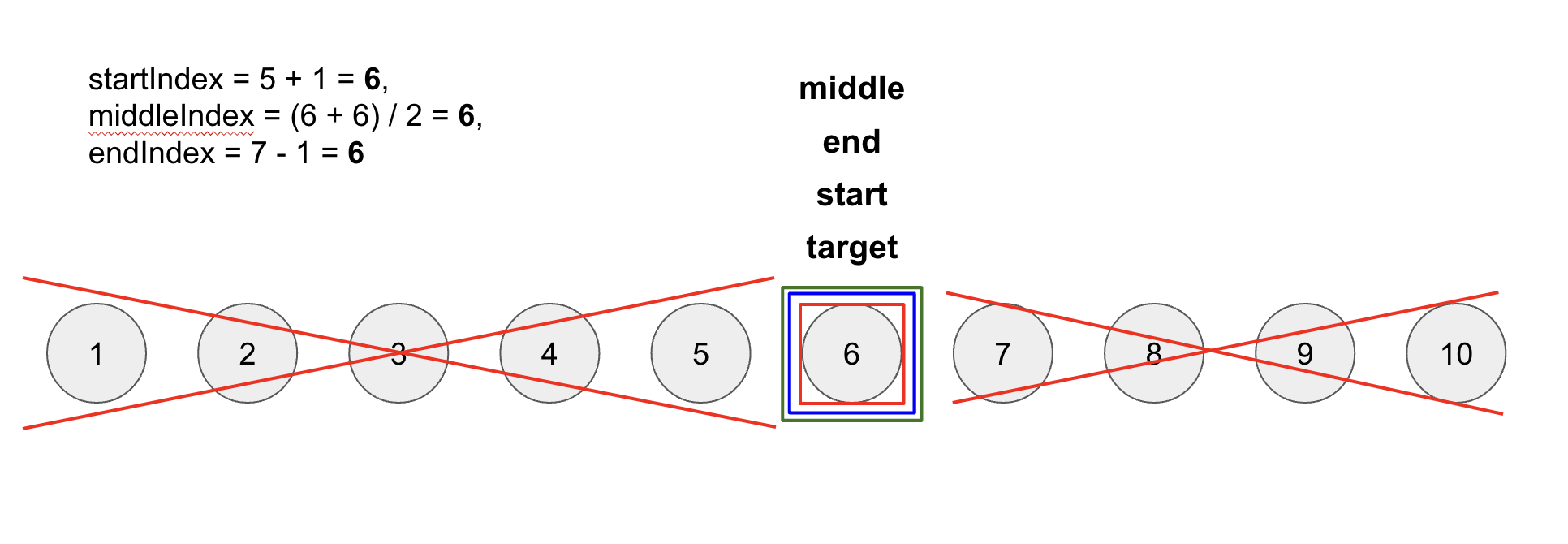
• middleIndex에 1을 더한 startIndex값은 6이고, middleIndex값은 6이 된다.

• 이제 arr[middleIndex] 값과 target의 값이 일치하므로 target의 index를 리턴하게 된다.

2. 이진 탐색의 Big O

---

• 이진 탐색의 Big O는 log n이다.

• 배열 arr의 크기를 2배로 늘릴 때마다 검색 단계는 1단계씩 증가한다.

• 배열의 요소가 16개라면 찾는 값이 배열에 없거나 제일 마지막 단계에서 찾을 경우 최대 4단계까지 걸린다. 즉, 밑을 2로 하는 log 16은 4기 때문에 최대 4단계가 필요하다.

• 마찬가지로 배열의 요소가 32개라면 log 32는 5기 때문에 최대 5단계가 필요하다.