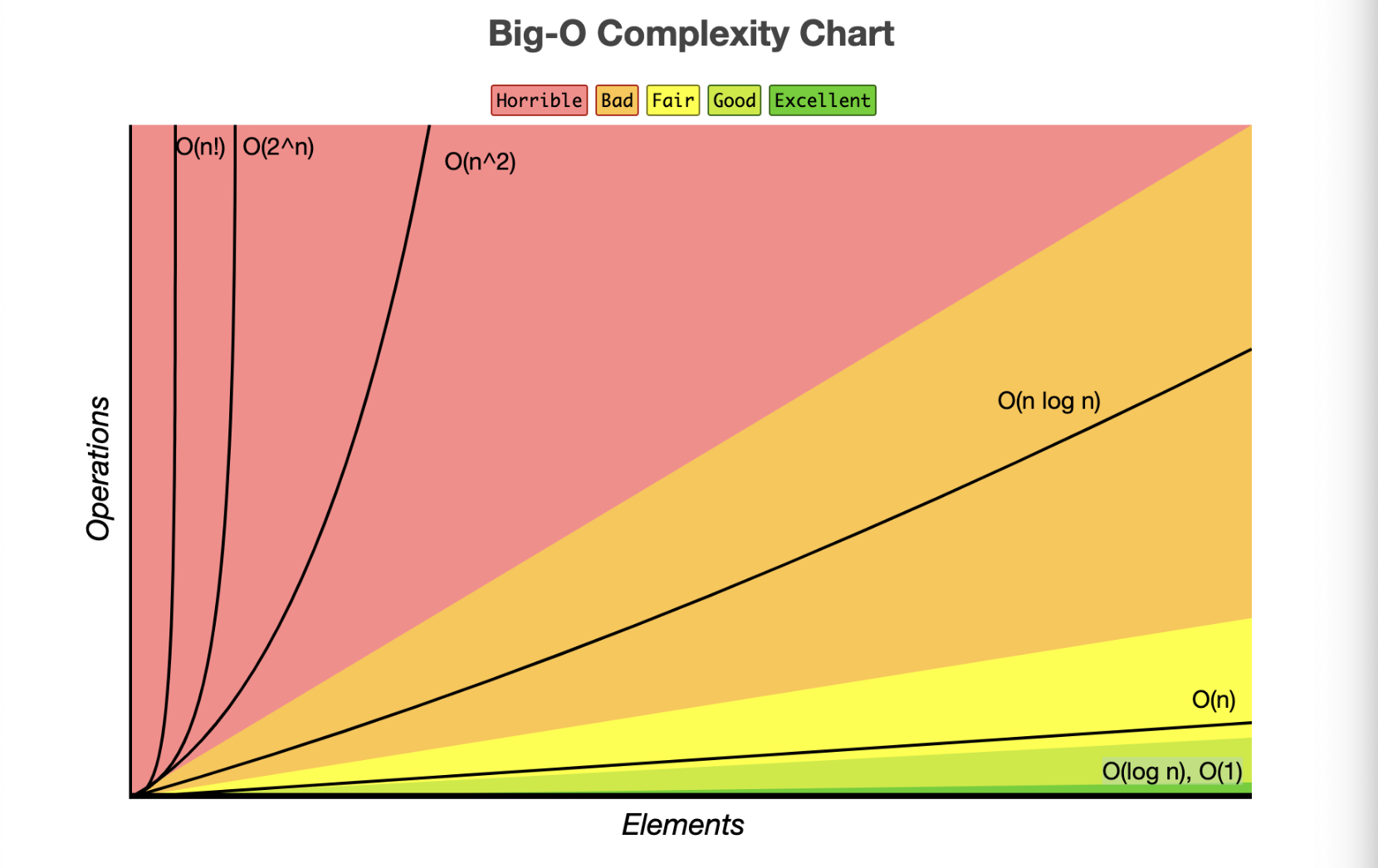
1. 빅오 표기법(Big O Notation)

---

• 빅오 표기법은 알고리즘의 시간 복잡도를 나타내는 표기법을 말한다.

2. 시간 복잡도(Time Complexity)

---

• 시간 복잡도란 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?를 의미한다.

1) O(1) - constant complexity

• O(1)은 입력값에 상관없이 일정한 실행시간이 걸리는 알고리즘을 말한다.

// 연산을 곱셈, 덧셈, 나눗셈 3번(`O(3)`)만 하면 되기 때문에 계산 속도가 빠르다.
// 즉, n의 값에 영향을 받지 않는다.
function addAll(n) {
    return n * (n + 1) / 2;
}

// 해당 인덱스에 바로 접근하여 계산하므로 arr가 아무리 커져도 상관없다.
function O_1_algorithm(arr, index) {
	return arr[index];
}

console.log(O_1_algorithm([1, 2, 3, 4, 5], 1)); // 2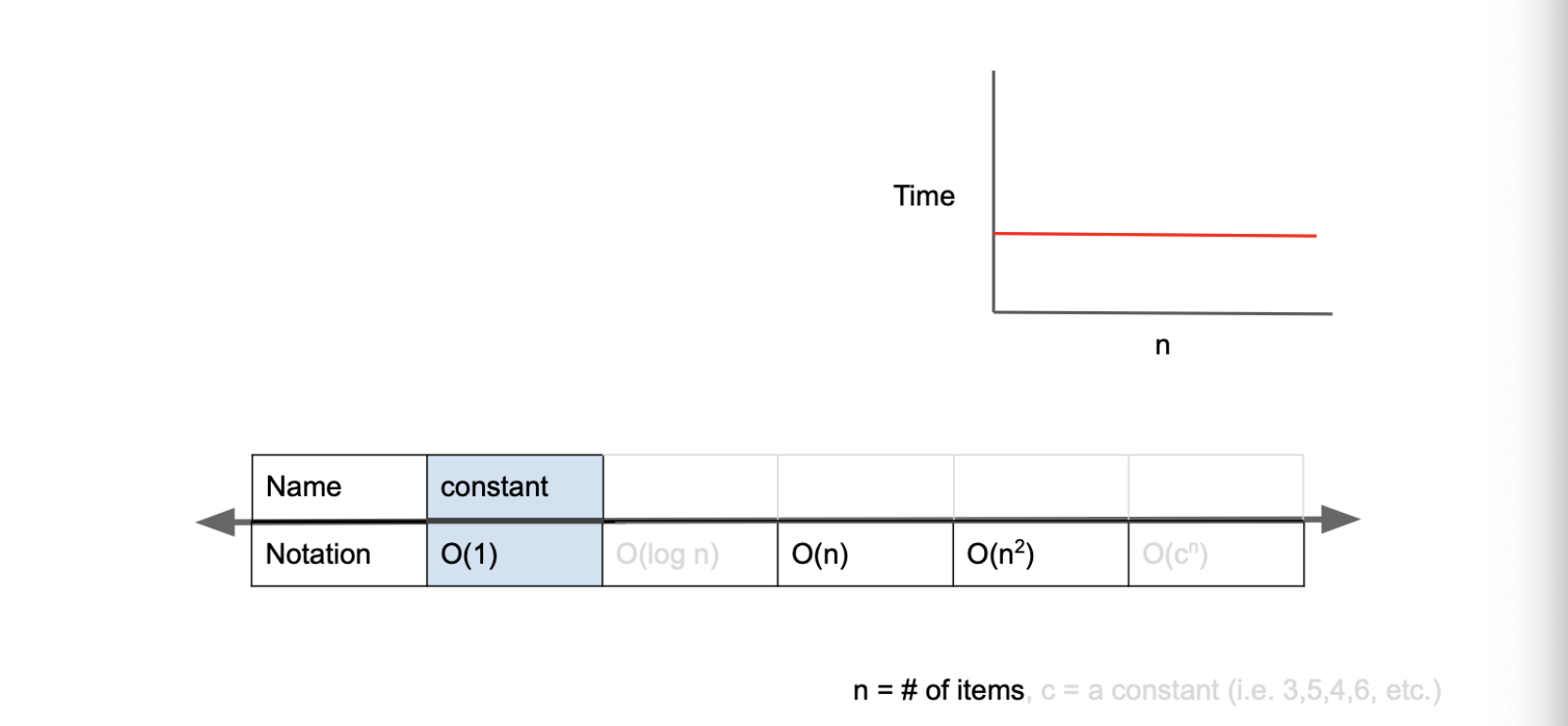

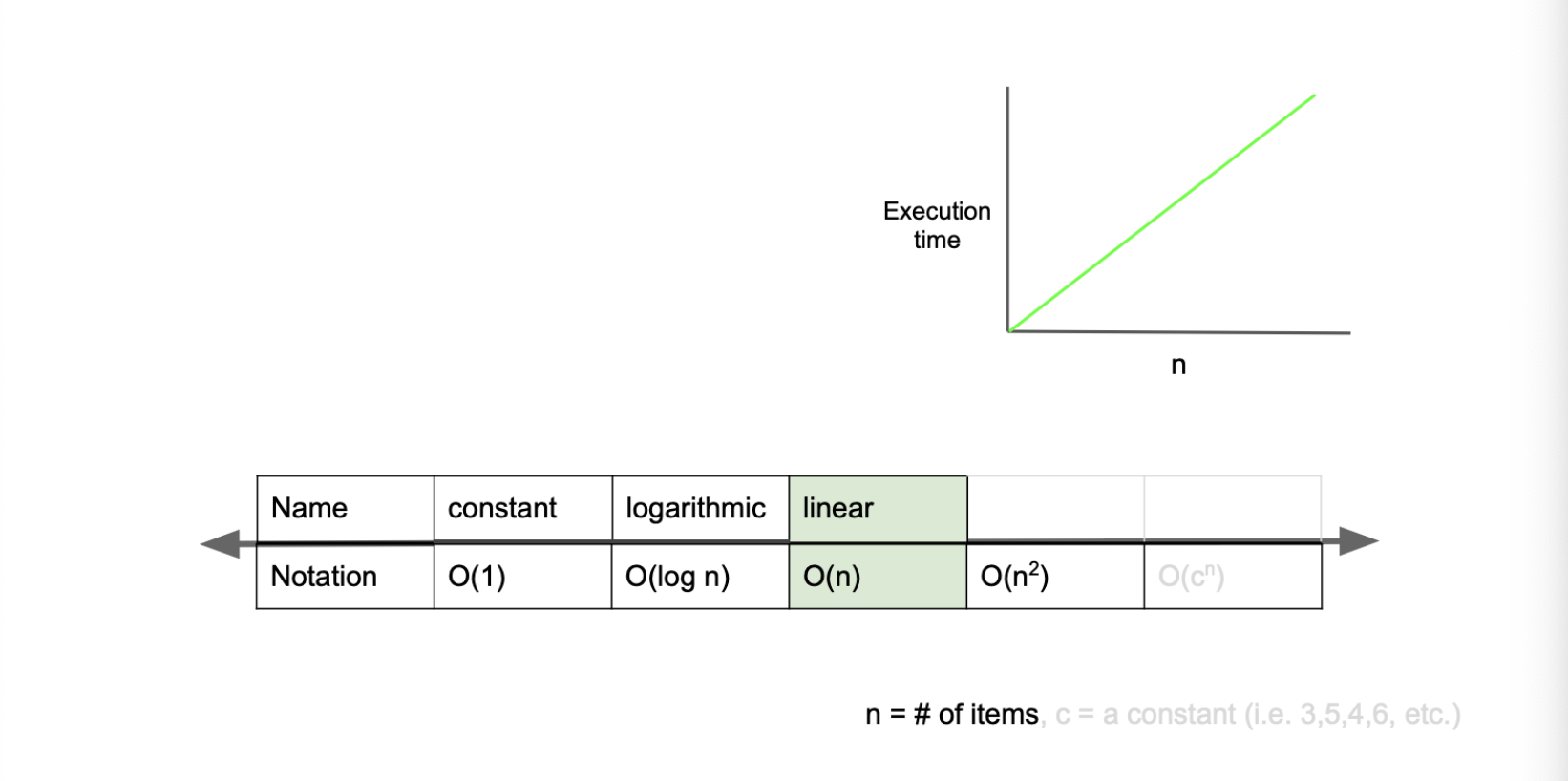
2) O(n) - linear complexity

• O(n)은 입력값이 증가함에 따라 실행시간 또한 같은 비율로 증가하는 알고리즘을 말한다.

• 모든 입력값을 적어도 한 번 이상 살펴봐야 하기 때문에 n의 값에 영향을 받아 n이 커질수록 실행시간도 비례하여 늘어난다.

• 입력값이 커지면 커질수록 계수(n 앞에 있는 수)의 의미(영향력)가 점점 퇴색되기 때문에, 같은 비율로 증가하고 있다면 2배가 아닌 5배, 10배로 증가하더라도 O(10n)이 아닌, O(n)으로 표기한다.

// 1 부터 num까지의 숫자 합을 구하는 과정에서 n의 수 만큼 연산해야 되기 때문에
// n이 극단적으로 큰 수가 들어온다면 연산이 오래 걸리게 된다.
function addAll(n) {
    let total = 0;

    for (let i = 1; i <= n; i++) {
        total += i;
    }
    return total;
}

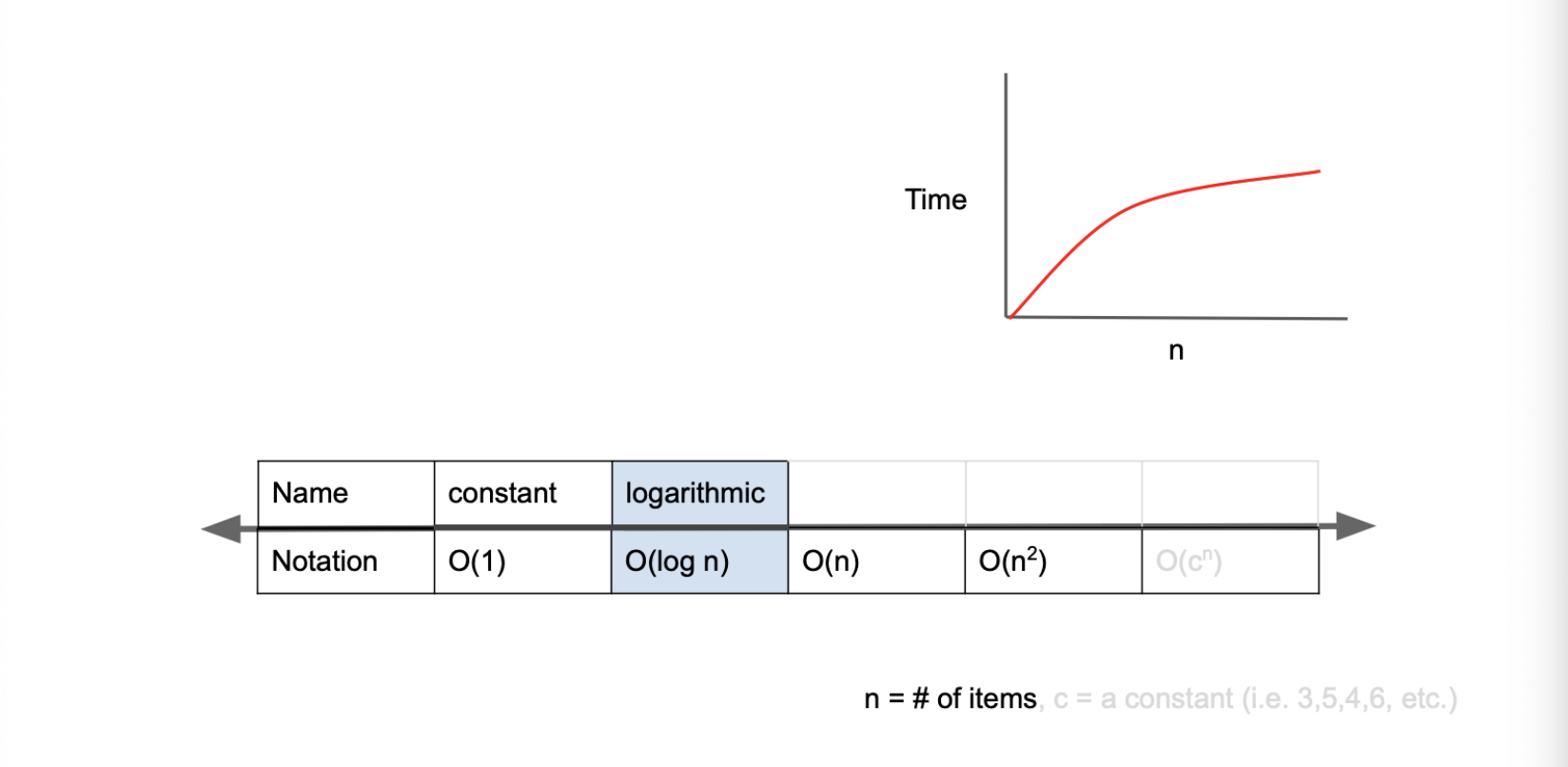
3) O(log n) - logarithmic complexity

• O(log n)은 빅오 표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다.

• 이진 탐색(Binary Search) 알고리즘의 시간 복잡도는 O(log n)이다.

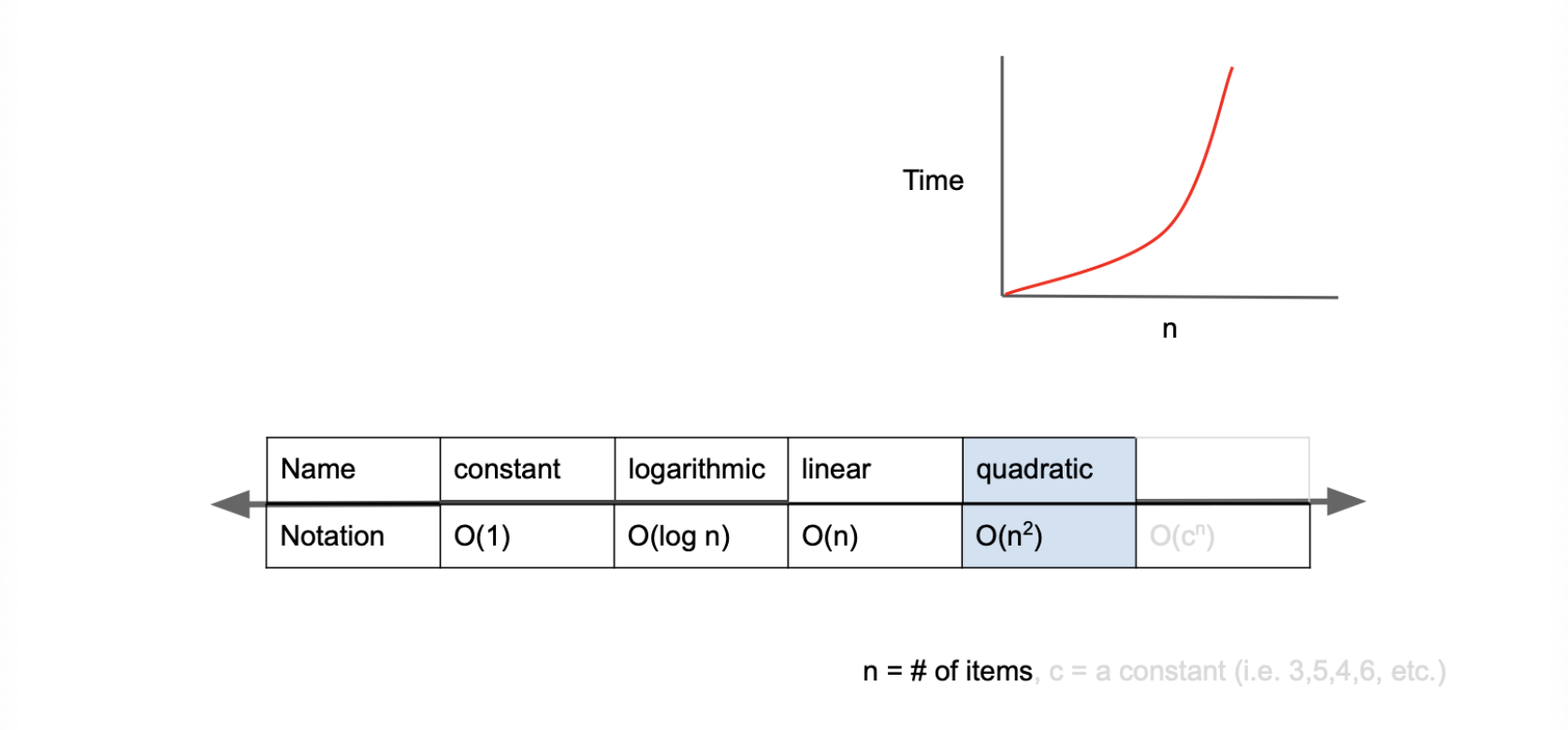
4) O(n^2) - quadratic complexity

• O(n^2)은 입력한 n개수의 제곱(n^2)만큼 수행된다. 즉, 입력값이 증가할 수록 실행시간이 제곱수의 비율로 증가한다.

• n이 커지면 커질수록 지수가 주는 영향력이 점점 퇴색되기 때문에 n3과 n5도 모두 O(n^2)로 표기한다.

// O(n)인 for문이 중첩으로 있기 때문에 O(n^2)이다.
// n이 2면 나올수 있는 경우의 수는 4고, n이 5면 25가 된다.
function printAllPairs(n) {
    let result = []

    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n; j++) {
            result.push([i, j])
        }
    }
    return result;
}

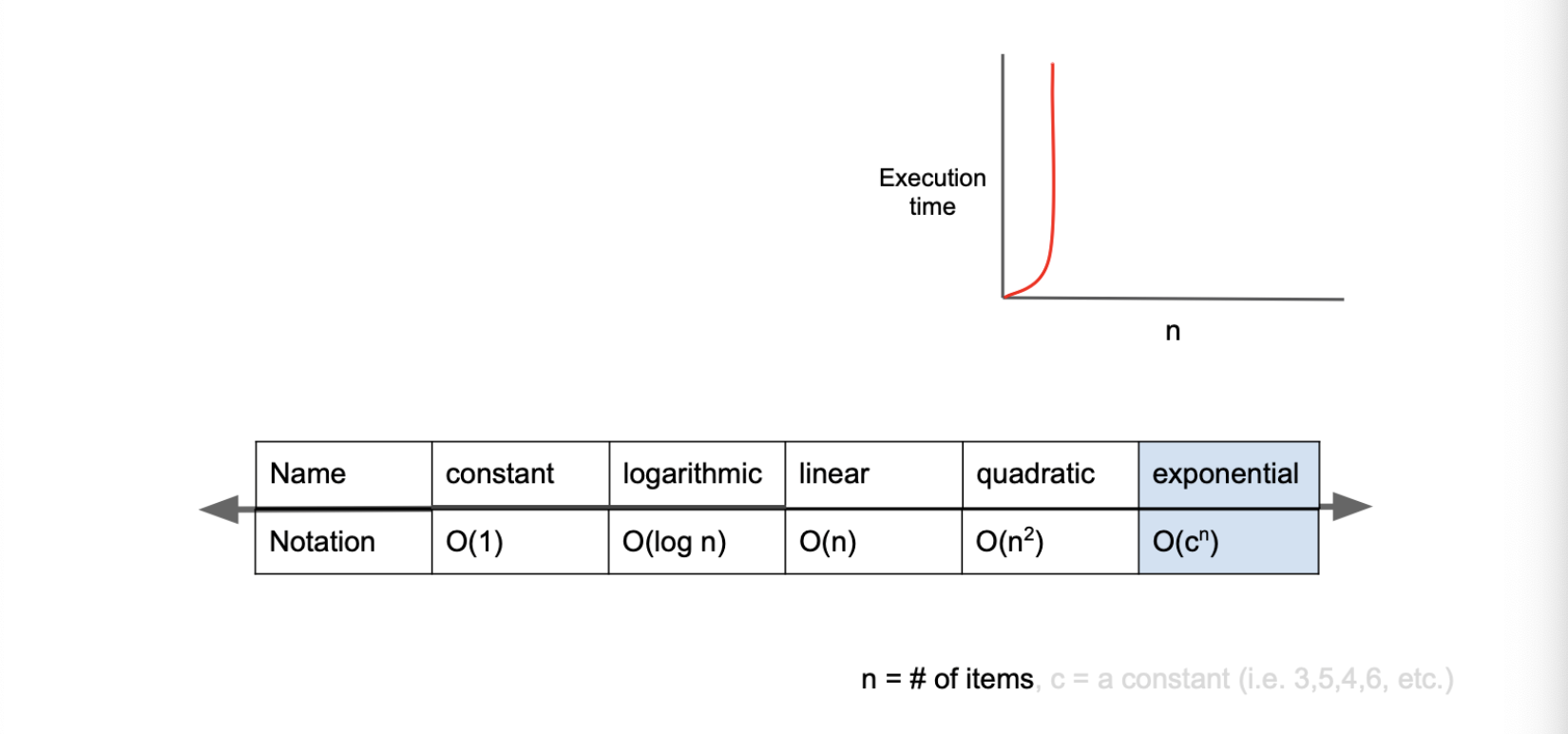
5) O(2^n) - exponential complexity

• O(2^n)은 빅오 표기법 중 가장 느린 시간 복잡도를 가진다.

• 재귀로 구현하는 피보나치 수열 알고리즘의 시간 복잡도는 O(2^n)이다.

3. 공간 복잡도(Space Complexity)

---

• 공간 복잡도는 입력이 커질수록 알고리즘이 얼마나 많은 공간(메모리)을 차지 하는지를 나타내는 것을 말한다.

• 동적 계획법(Dynamic Programming)과 같은 알고리즘이나 하드웨어 환경이 매우 한정되어 있는 경우 공간 복잡도가 중요해진다.

1) O(1)

• boolean, number, undefined, null은 O(1)의 공간 복잡도를 가진다.

• 아래의 예제를 공간 복잡도의 관점에서 보면 arr의 길이가 몇이든 상관없이 total이라는 변수에 arr의 모든 요소를 다 더하므로 total 변수와 i만 공간을 차지한다. 따라서 공간 복잡도는 O(1)이다.

function addAll(arr) {
    let total = 0;

    for (let i = 1; i <= arr.length; i++) {
        total += arr[i];
    }
    return total;
}

2) O(n)

• string은 O(n)과 Reference type들(Array, Object)은 일반적으로 O(n)의 공간 복잡도를 가진다.

• newArr의 길이는 arr의 길이에 비례해서 길어진다. 따라서 공간 복잡도는 O(n)이다.

function double(arr) {
    let newArr = [];

    for (let i = 0; i < arr.length; i++) {
        newArr.push(arr[i] * 2);
    }
    return newArr
}