1. 버블 정렬

---

• 버블 정렬의 개념은 배열을 오름차순으로 정렬할 때 더 큰 숫자가 한 번에 하나씩 뒤로 이동하는 것이다. 즉, 현재 보고 있는 요소가 다음 요소보다 크다면 둘의 순서를 바꾼다.

인덱스 변경 로직

function swap1(arr, index1, index2) {
    let temp = arr[index1];
    arr[index1] = arr[index2];
    arr[index2] = temp;
}

const swap2 = (arr, index1, index2) => {
    [arr[index1], arr[index2]] = [arr[index2], arr[index1]];
}

의사코드

1. 외부 반복문은 배열의 끝(마지막 인덱스)에서 부터 시작 인덱스까지 역순으로 루프를 시작한다.
2. 내부 반복문은 외부 반복문과 반대로 처음부터 시작하여 i 전까지 탐색한다.
3. arr[j]가 ar[j+1]보다 크면 두 값의 위치를 바꾼다.
4. 위 작업을 반복하여 최종 정렬된 배열을 반환한다.

• arr[j]가 바로 다음 요소인 arr[j + 1] 보다 크다면 둘의 위치를 바꾼다. 반복문을 한 바퀴 돌때마다 제일 큰 값은 배열의 끝으로 가게 되고, 이 때 마다 arr.length - 1 씩 검색 횟수가 줄어든다.

function bubbleSort(arr) {
    for (let i = arr.length - 1; i >= 0; i--) {
        for (let j = 0; j < i; j++) {
            if (arr[j] > arr[j + 1]) {
                let temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
    return arr;
}

console.log(bubbleSort([6, 5, 7, 4, 1, 3]));  // [1, 3, 4, 5, 6, 7]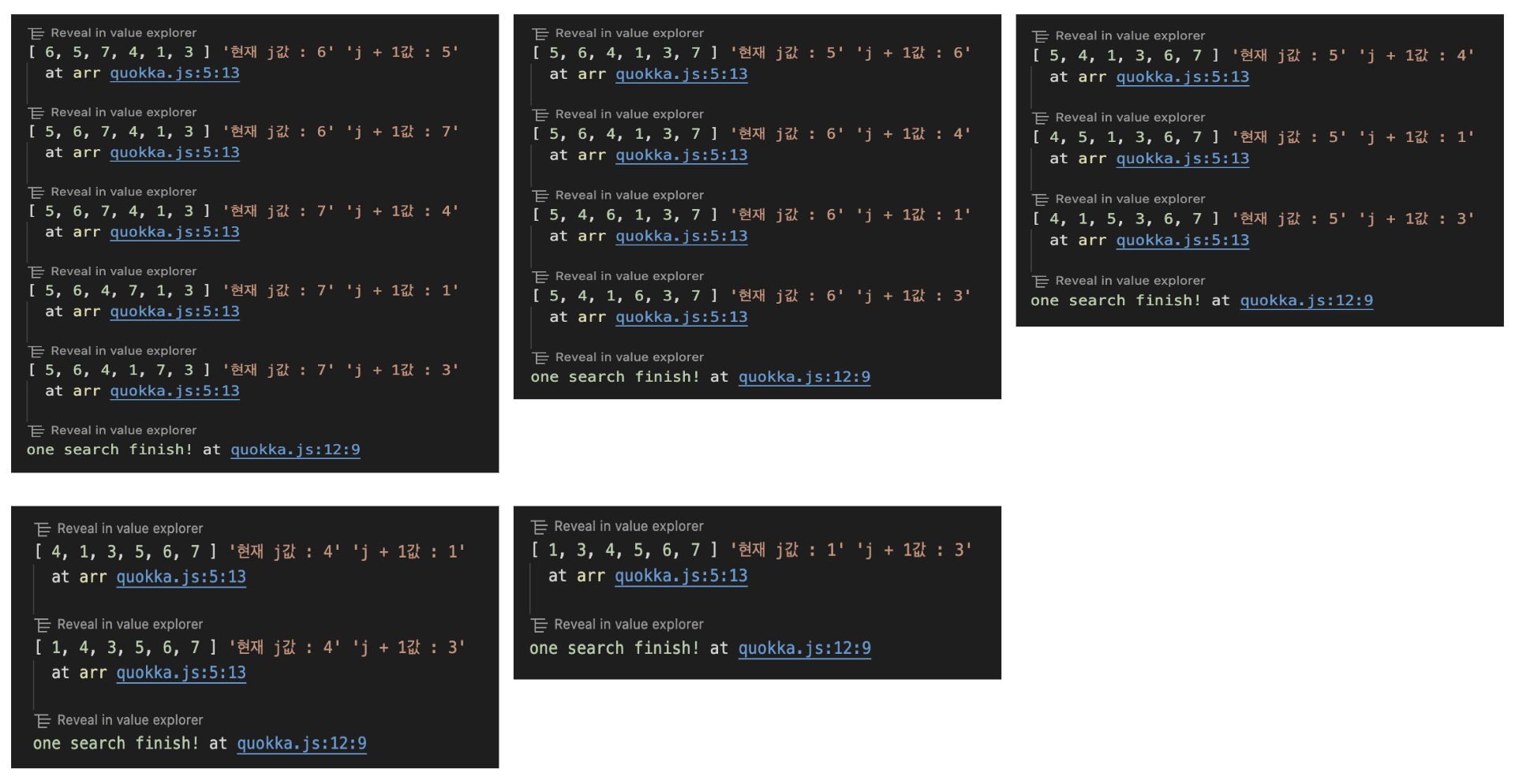

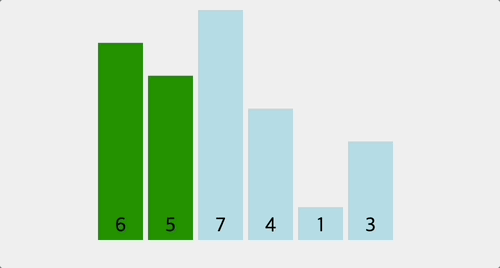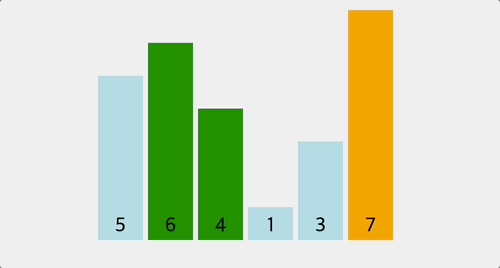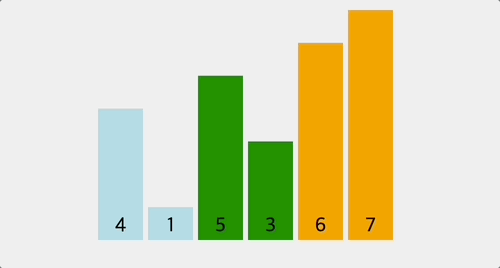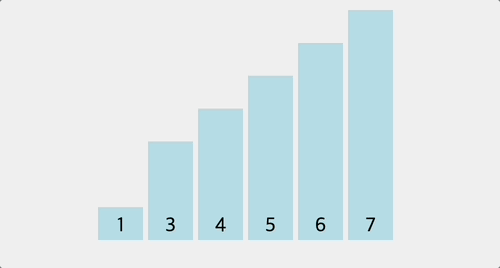
1) 최적화

---

• 이미 거의 정렬이 되어 있는 배열을 입력 받은 경우 정렬이 완료 된 시점에 코드를 실행 종료시키는 것이 좋다. 왜냐하면 정렬이 완료되어 순서를 바꿀 요소가 없는데도 코드는 계속 실행되기 때문이다.

• 아래 예제에서 교환이 발생하면 noSwap 변수의 값이 true에서 false로 변경되며 반복문이 계속 실행된다.

• 그러나 이미 정렬이 완료되어 있는 배열의 경우 처음 j 반복문에서 끝까지 돌았을 때 변경사항이 없으므로 교환이 발생하지 않아 noSwap 변수가 그대로 true인 상태로 반복문을 통과한다면 아래의 if 문으로 인해 반복문을 탈출하게 되고, 입력받은 이미 정렬된 arr를 그대로 리턴하게 된다.

function bubbleSort(arr) {
    for (let i = arr.length - 1; i >= 0; i--) {
        let noSwap = true;  // 교환 발생 여부 확인 변수
        for (let j = 0; j < i; j++) {
            if (arr[j] > arr[j + 1]) {
                let temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                noSwap = false;  // 교환이 발생하면 false로 변환
            }
        }
      // 교환이 발생하지 않는다면 반복문을 탈출한다.
        if (noSwap) {
            break;
        }
    }
    return arr;
}

console.log(bubbleSort([6, 1, 2, 3, 4, 5]));  // [1, 2, 3, 4, 5, 6]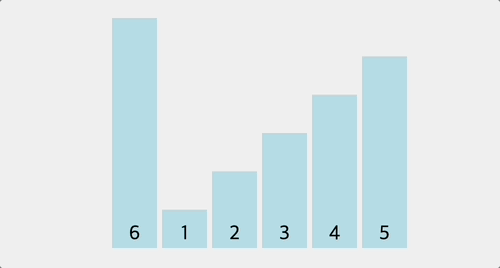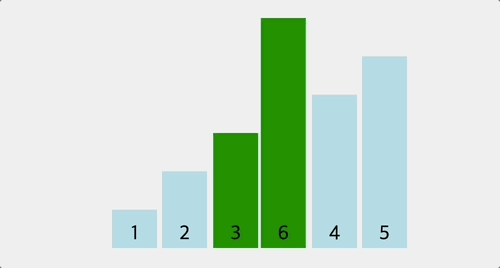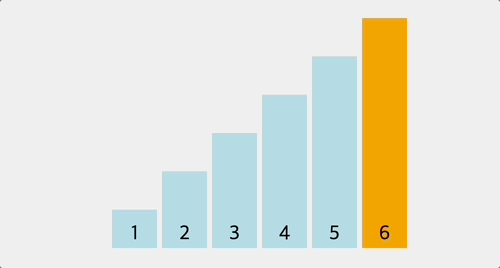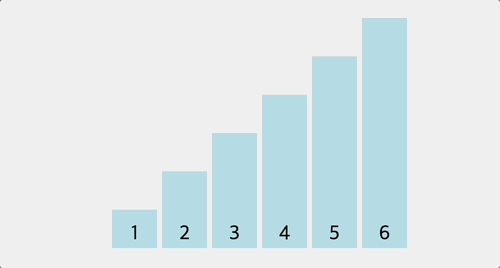

2. 버블 정렬의 Big O

---

• 버블 정렬의 Big O는 n^2이다.