[프로그래머스] 입국심사

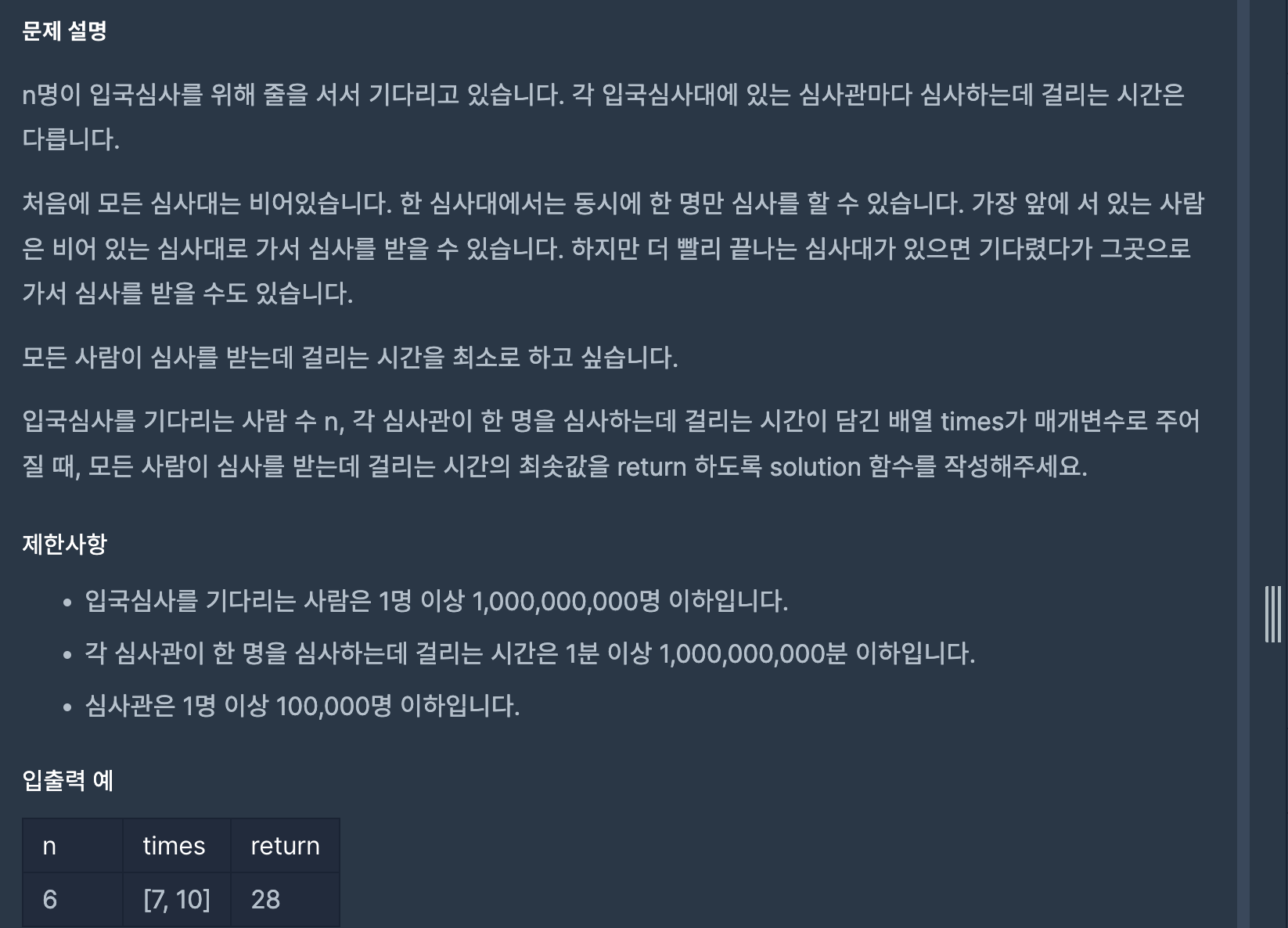
문제

[입국심사]

풀이

• 입국 심사를 기다리는 사람 수(n)와 심사관이 한 명 심사를 하는데 걸리는 시간(times[i])가 1,000,000,000이므로 O(n)을 넘으면 안됨. 엄청나게 큰 n과 특정값 구하기므로 일단 이진탐색을 생각할 수 있음

• 결국, 심사관의 배열 times를 순회하면서 풀어햐 한다. 최대 100,000이니까

• 모든 승객을 심사하는데 걸리는 최소값을 구하려면 생각해야 하는 것이, 심사에 소모되는 시간이 최소 몇 분이야여 모든 승객을 모두 심사할 수 있을까이다. 예제에 나온 n = 6, times = [7, 10]의 경우, 심사에 걸린 시간이 30분이어도 모두 심사할 수 있다. 하지만 20분이라면 5명 밖에 심사하지 못한다. 즉, 최소 시간을 탐색하면서 (이진탐색 시 mid 값) low와 high를 계속 수정해야 한다.

• 먼저 sort를 통해서 한 명 당 심사가 가장 오래 걸리는 값을 찾고, high 값에 할당한다

• 그리고 이진탐색 시작!

• time 배열을 순회하면서 mid / times[i])의 값, 즉 총 시간 중 심사관 한 명이 심사할 수 있는 승객의 수를 모두 구한다.

• 심사 가능한 승객의 수가 주어진 n보다 작다면 심사 시간을 늘려야 하니까 low를 올리고

• 심사 가능한 승객의 수가 n보다 같거나 크면 심사 시간을 줄인다. 이때부터는 mid가 answer가 될 수 있는 가능성이 있으므로 answer에 mid를 할당한다. (아까 말했던 것처럼 예제에서 30분분도 모든 승객을 심사하는 시간을 커버한다. 문제에서 원하는 것은 최소 시간이므로 심사 가능한 승객의 수가 mid와 같더라도 계속 이진탐색을 해야한다)

코드

import java.util.Arrays;

class Solution {
    public long solution(int n, int[] times) {
        Arrays.sort(times);
        
        long answer = 0;
        long low = 1;
        long high = (long) n * times[times.length - 1];
        
        while(low <= high){
            long mid = (low + high) / 2;
            long coveredPassenger = 0;
            
            for(int i = 0; i < times.length; i++){
                coveredPassenger += Math.floor(mid / times[i]);
                if(coveredPassenger >= n) break;
            }
            
            if(coveredPassenger >= n){
                answer = mid;
                high = mid - 1;
            } else {
                low = mid + 1; 
            }
        }
            
        return answer;
        
        
    }
}

정리

• 문제를 이해하는데 굉장히 오래 걸렸음
• 이진탐색 문제들은 직관적으로 이해가 잘 안 되는 듯..
• 어떤 값을 최소값으로 할 것이냐(low냐 mid냐)에서 헷갈렸음. 아직 문제를 완벽히 이해한 것이 아닌듯