- 문제
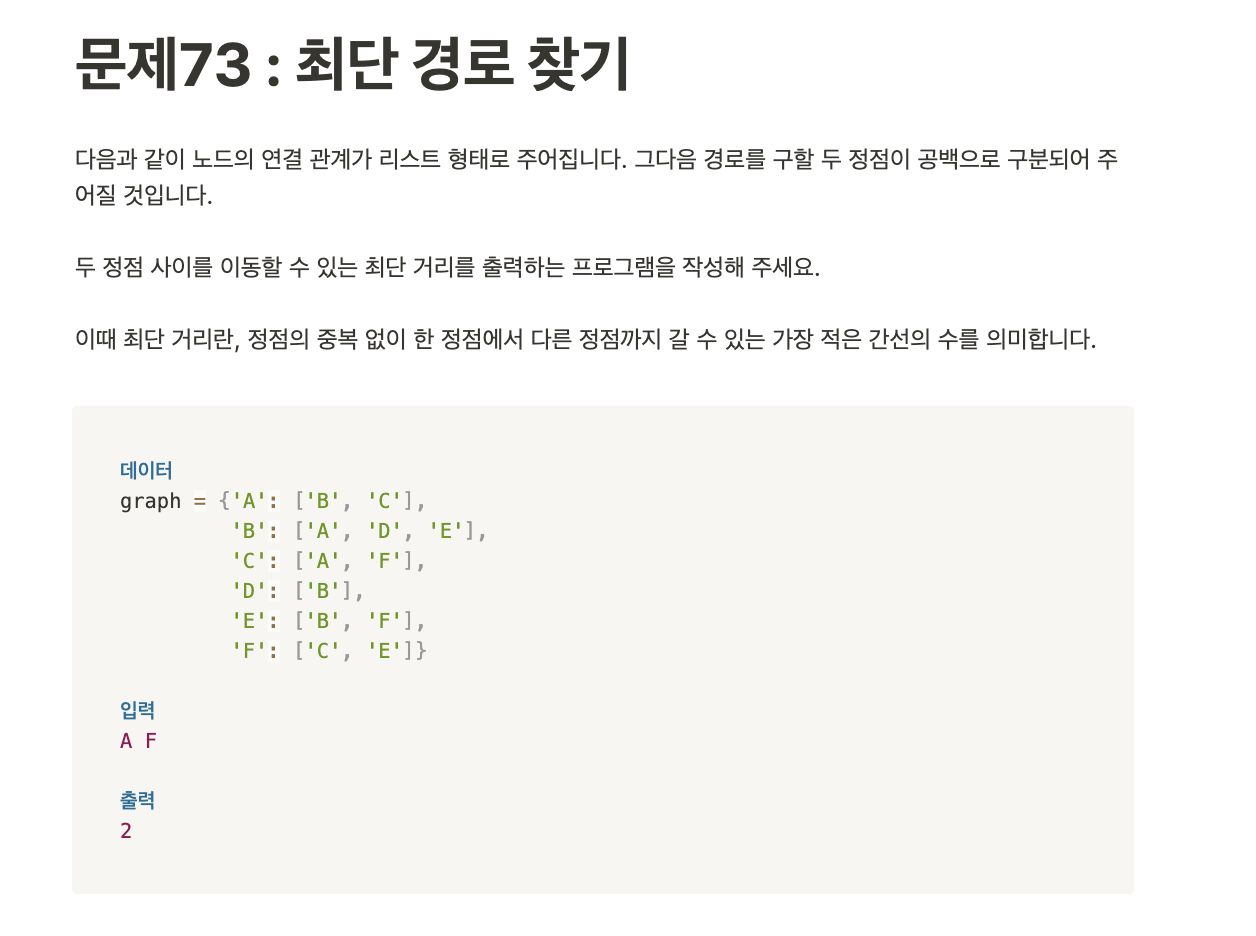
- 내 풀이
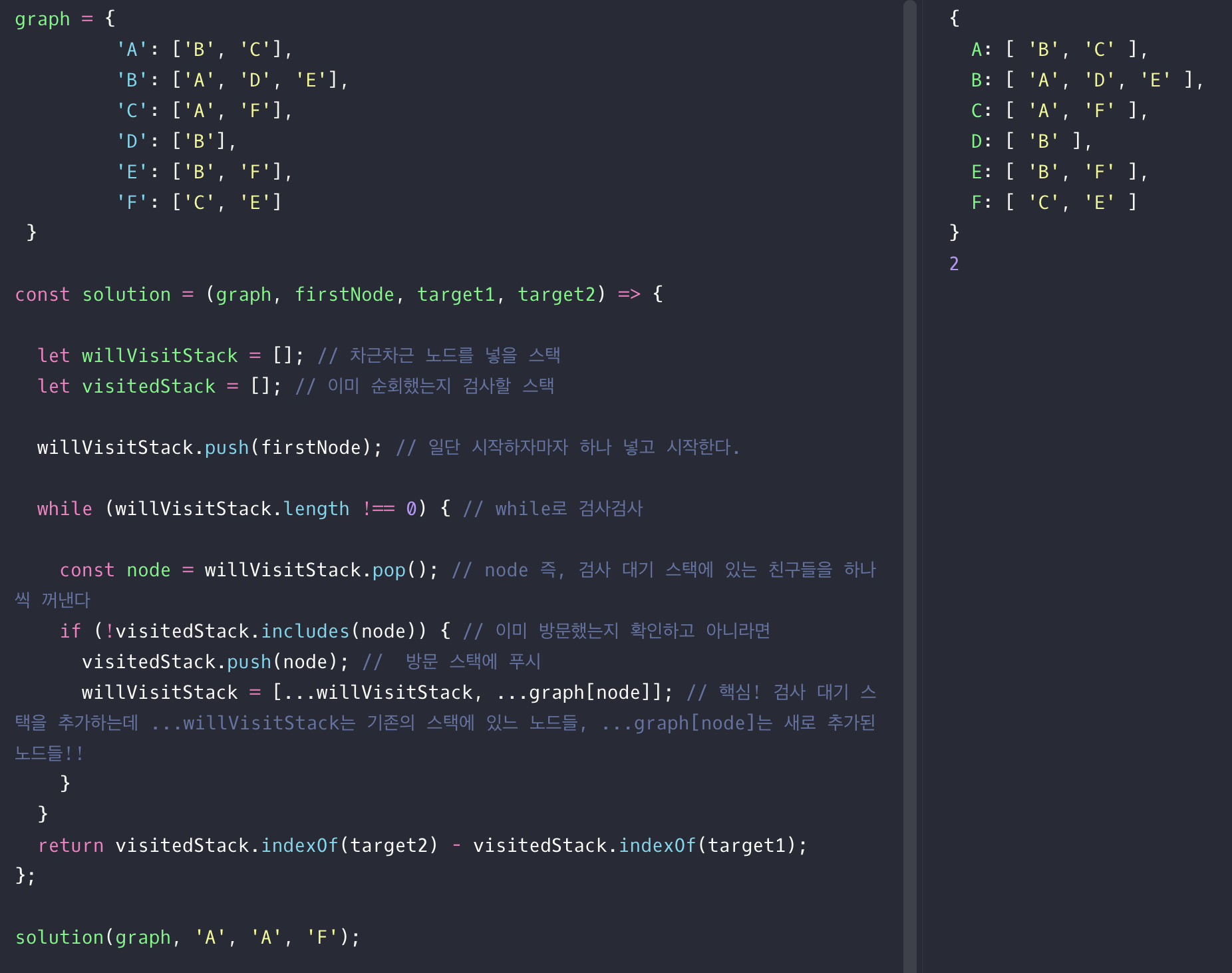
일단 DFS를 아주 확실히, 그러니까 클래스로도 구현할 수 있는 정도의 깜냥이 안 되기 때문에 최단 경로 구하는 문제 감도 안 왔다. 다른 블로그나 코드를 봐도 이해가 안 되는 것은 아직 이쪽 알고리즘 세계에 대한 이해가 많이 많이 부족하기 때문이라 생각함!
여태까지 알고리즘 문제는 내가 생각한 대로 코드로 풀면 답이 나왔는데 이건 완전히 다른 세계라는 느낌이었다. 나의 부족함을 아주 아주 적나라하게 마주친 것이다!! 그러니까 여태까지는 일차원적인 느낌이라 내 머릿속으로 들어오는 인풋과 손으로 치는 아웃풋이 동일했는데 dfs, bfs는 이차원적이라 머릿속에서 스택에 담았다 뺏다 큐에 넣었다 상상을 펼쳐야 하는 아주 아주 어려운 느낌을 받아 잠시(3분) 좌절했지만 금방 다시 일어나서 코드를 쳤다. 늘 그랬듯이..
일단 그래서 dfs로 정말 간단하게 풀어서 인덱스를 빼줬다. 이건 틀렸어 틀렸지만 어쩔 수 없다.. 그럼 해답을 보면서 차근차근 부수자!
- 답안

- 답안 부수기
일단 위의 그래프를 그림으로 표현하면
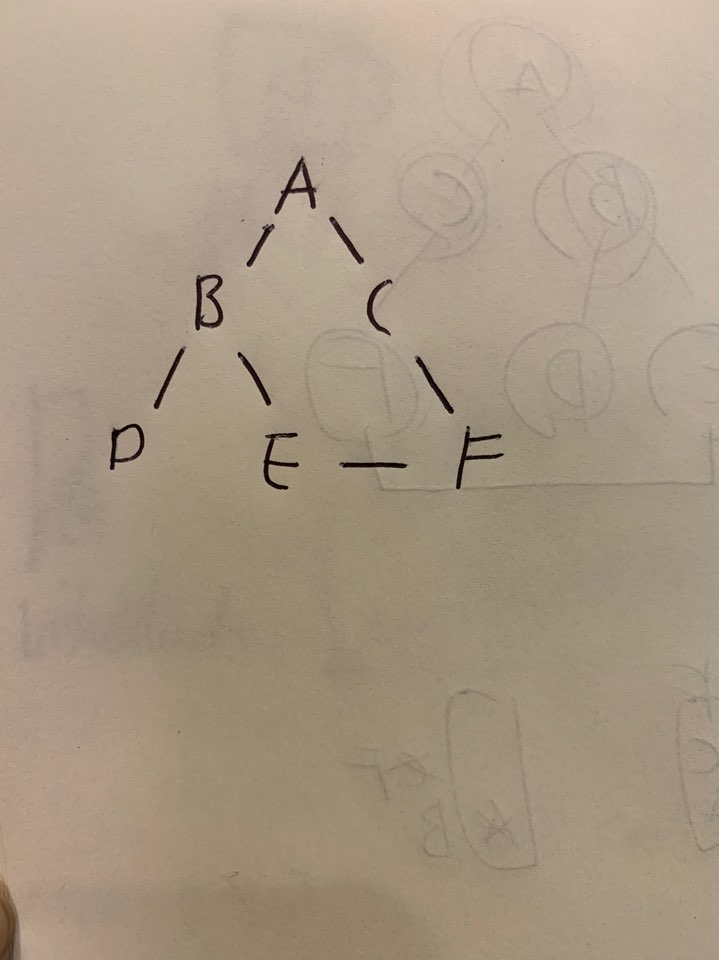
이런 깜찍한 모습이 나온다. 문제에서 주어진 A에서 F로 갈 수 있는 방법은 [A, C, F], [A, B, E, F] 인데 이 중 최단 거리를 구하는 것
코드
let queue = [start];
let visited = [start];
let count = -1;일단 큐랑 스택에 start 노드를 넣고 시작한다. count는 아마 visited 스택에 노드가 쌓일 때 카운트를 해주는 것 같다. 다익스트라를 잘 모르지만 가중치? 같은 원리가 아닐까. 아무튼 카운트가 있느 것 보니 한 정점에서 한 정점에 갈 경우에 대해 카운트를 때려서 모든 경우를 구하는 것으로 추측한다 일단은
while (queue.length !== 0) {
count += 1;
let size = queue.length;
// code...
}while 돌려서 한 루프가 시작할 때 카운트 올려주고 queue.length를 사이즈에 할당한다.
while (queue.length !== 0) {
count += 1;
let size = queue.length;
for (let i = 0; i < size; i++) {
let node = queue.splice(0, 1);
if (node == end) {
return count;
}
}이제 무언가 시작되는데 while문 안에서 for문이라 흥미진진하다. size만큼 for문을 돌린다. 일단 queue에 들어있는 노드를 splice로 하나 뺀다. 이제 중요한 것은 node, 즉 방금 queue에서 뺀 node와 end가 같으면 count를 반환하는 것이다.
for (let next_node in graph[node]) {
if (!visited.includes(graph[node][next_node])) {
visited.push(graph[node][next_node]);
queue.push(graph[node][next_node]);
}
}이제 핵심부분인데 grpah[node] 즉, 어떤 노드에 인접한 노드를 for in문 돌린다. 그리고 만약 방문 stack에 그 노드가 없으면 visited, queue에 해당 노들을 넣는다.
- 일단 여태까지 흐름을 코드로 살펴보자!
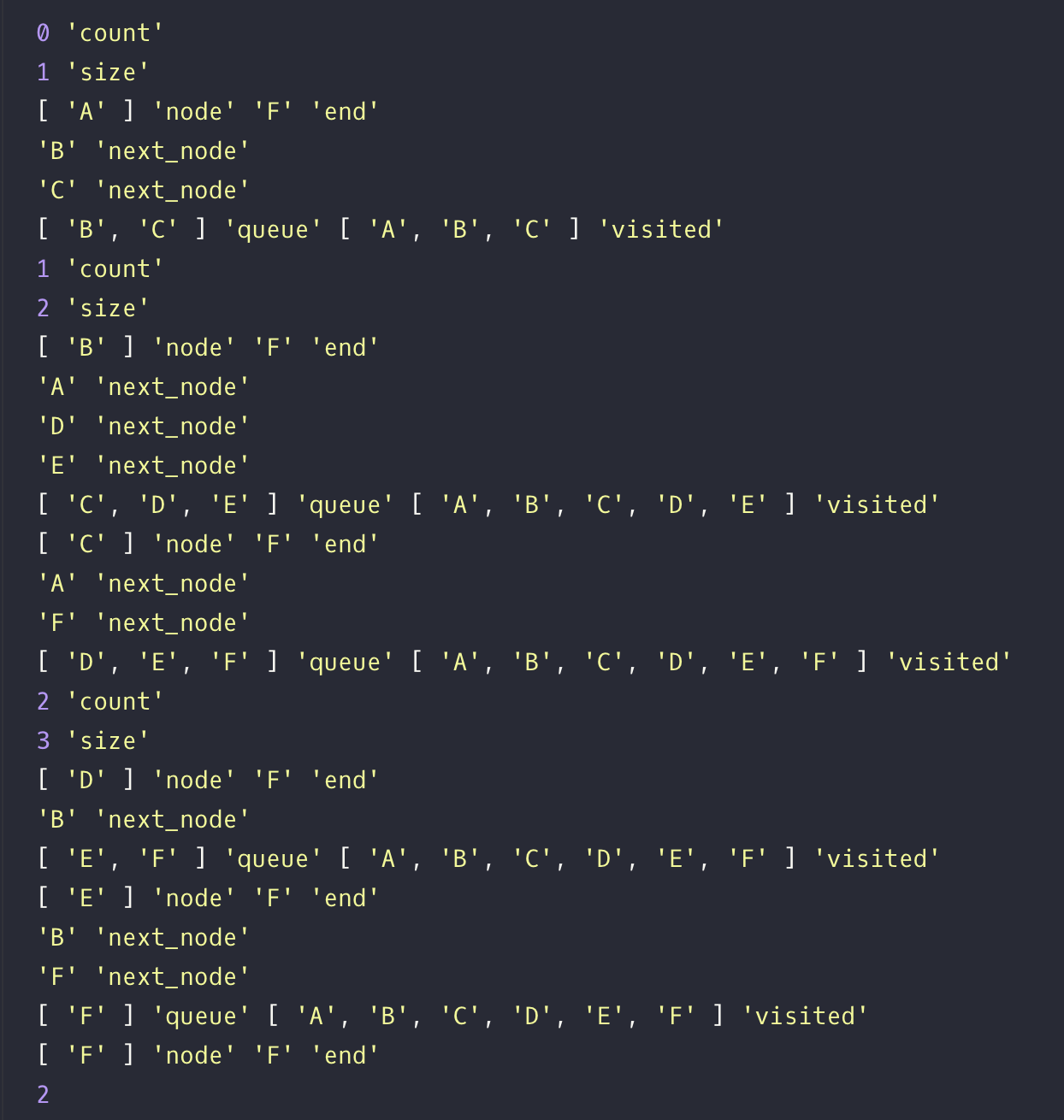
queue = [A] -> [B, C], visited = [A] -> [A, B, C]
while 1회차에 count는 0이 되고 size는 1이다. for문으로 queue에 첫 번째 노드, 즉 A를 빼서 비교한다. node와 end가 다르기 때문에 for in문으로 넘어간다. next_node는 B와 C다. visited에 이 노드들이 없으므로 visited와 queue에 노드들을 넣는다.
queue가 방문할 노드들이고 stack이 방문했던 노드들이라고 한다면 B,C는 아직 방문을 안 했는데 stack에도 동시에 넣는다는 것이 핵심이라고 생각!
queue = [B, C] -> [D, E, F], visited = [A, B, C] -> [A, B, C, D, E, F]
count는 1로 오르고 size도 2가 되었다. 아! for문을 돌리는 이유는 모든 경로수를 검사하는 게 아니라 방문할queue가 도착지인지를 검사해서 바로 함수를 종료하는 것! B와 C 모두 도착지가 아니니까 for in으로 넘어간다. B는 큐에서 빠지고 B의 인접 노드들을 queue와 stack에 넣는다.
이제 C의 인접 노드인 A, F를 본다. A는 이미 stack에 있으니까 패스. 어라? F네? 일단 F를 queue에 넣는다.
queue = [D, E, F] -> [D, E, F], visited = [A, B, C, D, E, F] -> [A, B, C, D, E, F]
아침이 밝았다. count가 2되고 size도 queue에 [D, E, F]가 있으니 3이다. 이제 D를 살펴보고 목적지가 아니니 for in으로 돌린다. 인접 노드는 B인데 이미 stack에 있으니 바로 패스. E를 살펴본다. 목적지가 아니니 for in. 인접 노드는 B와 F. B, F는 있으니까 패스하고 마지막 F!
F는 바로 목적지 if에 걸려서 count 리턴!!!!
이렇게 정답은 2다. 처음에 생각했을 때 모든 경우를 다 보고 가장 적은 수를 고르는 줄 알았는데 인접 노드들만 살펴보면 된다! 매우 매우 매우 신기해. 요 며칠은 최단거리만 파야지.
출처 : 제주코딩캠프