[프로그래머스] 합승 택시 요금

문제

합승 택시 요금

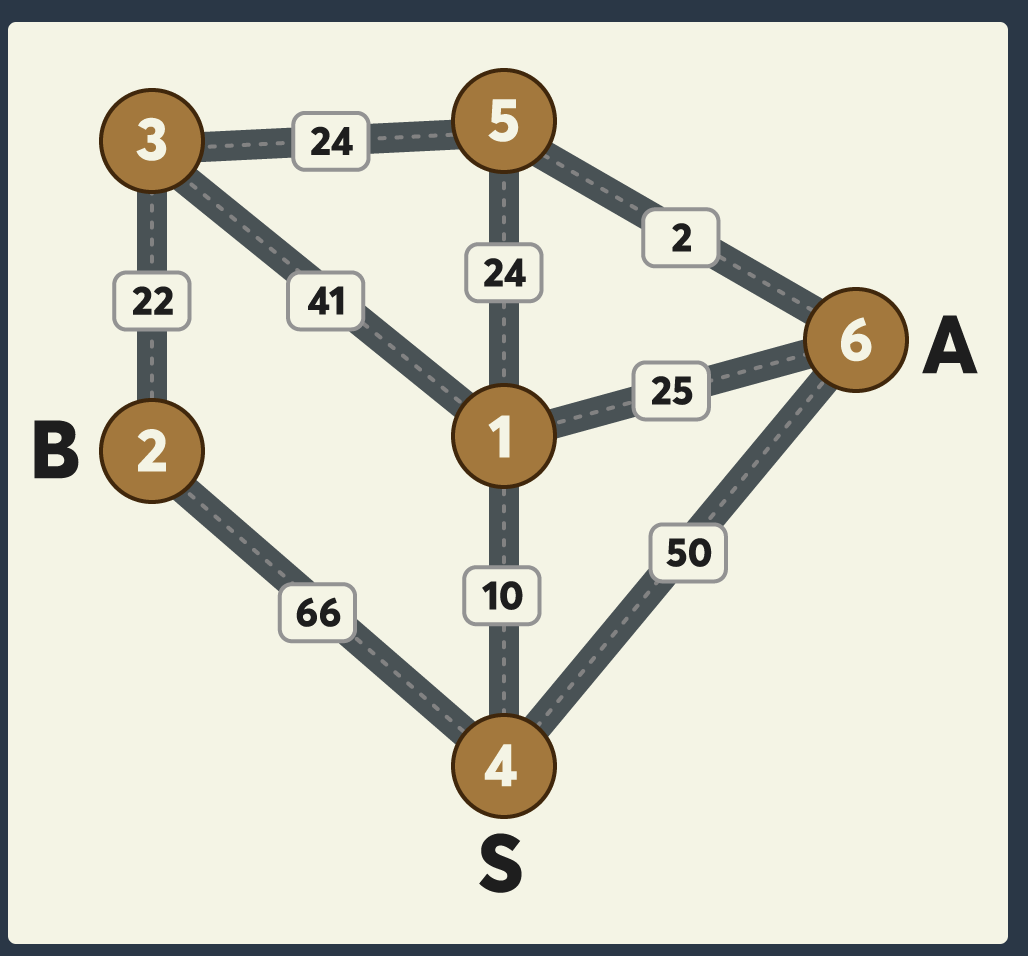
4→1→5 : A, B가 합승하여 택시를 이용합니다. 예상 택시요금은 10 + 24 = 34원 입니다.
5→6 : A가 혼자 택시를 이용합니다. 예상 택시요금은 2원 입니다.
5→3→2 : B가 혼자 택시를 이용합니다. 예상 택시요금은 24 + 22 = 46원 입니다.
A, B 모두 귀가 완료까지 예상되는 최저 택시요금은 34 + 2 + 46 = 82원 입니다.

풀이

• 가중치가 있는 그래프의 최단 거리이므로 다익스트라 아니면 플로이드임
• 합승이라는 제약조건이 있어서 모든 정점에 대한 A, B의 최단 거리를 구해야하므로 플로이드
• 모든 정점에 대해 S에서 출발했을 때 최단 거리와 그 정점에서 A, B로 갔을 때 최단 거리를 각각 구해 그 중 최소값을 찾으면 됨
• 정점은 최대 200이므로 O(n3)도 괜찮다

코드

function solution(n, s, a, b, fares) {
  let graph = Array.from({ length: n + 1 }, () => Array(n + 1).fill(Infinity));

  for (let i = 0; i < fares.length; i++) {
    const [start, end, w] = fares[i];
    graph[start][end] = w;
    graph[end][start] = w;
  }

  for (let i = 1; i <= n; i++) {
    graph[i][i] = 0;
  }

  for (let k = 1; k <= n; k++) {
    for (let i = 1; i <= n; i++) {
      for (let j = 1; j <= n; j++) {
        if (graph[i][j] > graph[i][k] + graph[k][j]) {
          graph[i][j] = graph[i][k] + graph[k][j];
        }
      }
    }
  }

  let min = Infinity;

  for (let node = 1; node <= n; node++) {
    min = Math.min(min, graph[s][node] + graph[node][a] + graph[node][b]);
  }

  return min;
}

정리

플로이드 라는 건 금방 떠올렸는데, 합승 구간을 제외하는 것을 쉽게 생각하지 못 했음