목차
- Fancier Optimization
- Regularization
- Transfer Learning
1. Optimization

- 가중치 W에 대한 손실함수 L은 가중치가 얼마나 좋은지 나쁜지 평가한다.
(1) Stochastic Gradient Descent
1) Gradient Descent
- Loss functioin에서 현 weight의 기울기(gradient)를 구하고 loss를 줄이는 방향으로 업데이트해 나가는 방향으로 학습
- 에러를 줄이는 방향으로 정해진 스텝량(Learning Rate)을 곱해서 weight를 이동시킨다.
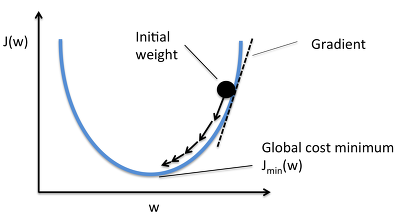
- GD 수식

- GD 단점
- 최적값을 찾기 위해(learning rate만큼 한번 걷기 위해) 모든 데이터셋을 넣어 학습해주어야 한다.
- 학습이 오래걸린다.
2) Stochastic Gradient Descent
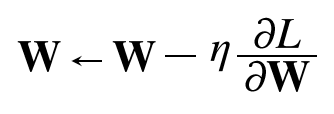
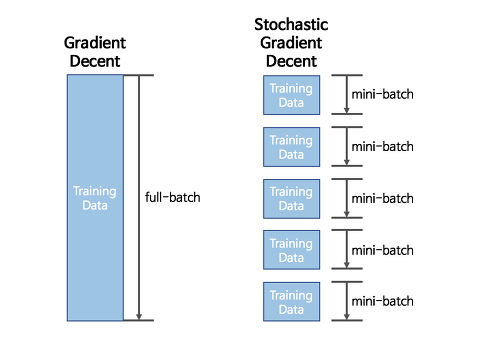
- Mini batch로 나눠 조금만 훑어보고 GD를 수행한다.
-
GD와 SGD 비교
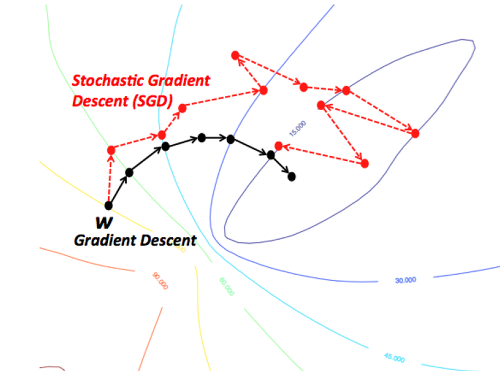
- 일부 데이터만을 사용해 학습해서 최적의 방향으로 학습이 진행되지는 않는다.
-
SGD 코드
# Stochastic Gradient Descent
while True:
weights_grad = evalute_gradient(loss_fun, data, weights) # mini-batch에서 loss 계산
weights += step_size * weights_grad # gradient 반대방향으로 parameter 업데이트- Stochastic Gradient Descent vs Mini-Batch Stochastic Gradient Descent
- Stochastic GD
- Batch size를 1로 설정
- Mini-Batch Stochastic GD
- Batch size 를 하이퍼 파라미터로 사용 (Batch_size=k)
- Stochastic GD
1) SGD의 문제점
-
Mini batch를 통해 학습시킬 때 최적의 값을 찾아가는 방향이 뒤죽박죽이다.
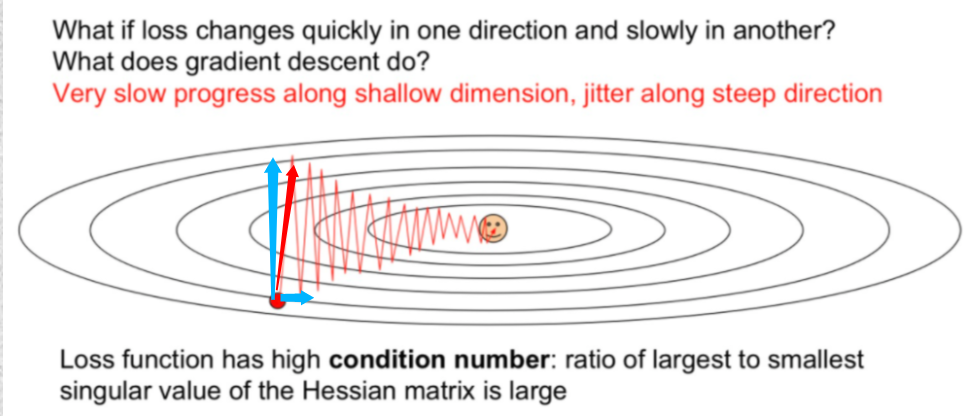
- 그래프와 등고선
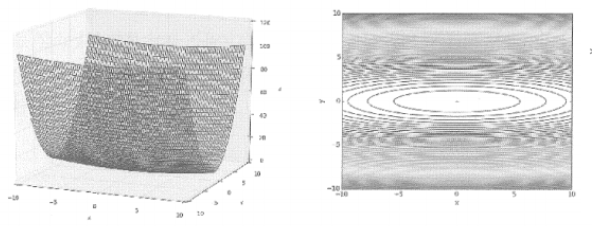
- 그래프와 등고선
-
Local minimum, Saddle point
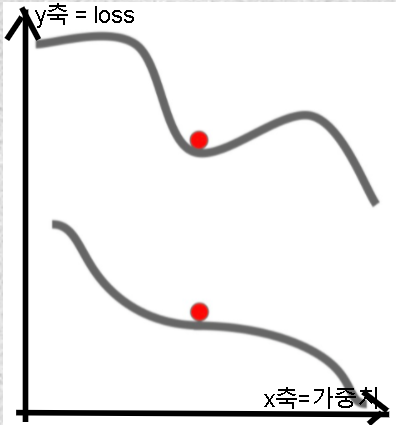
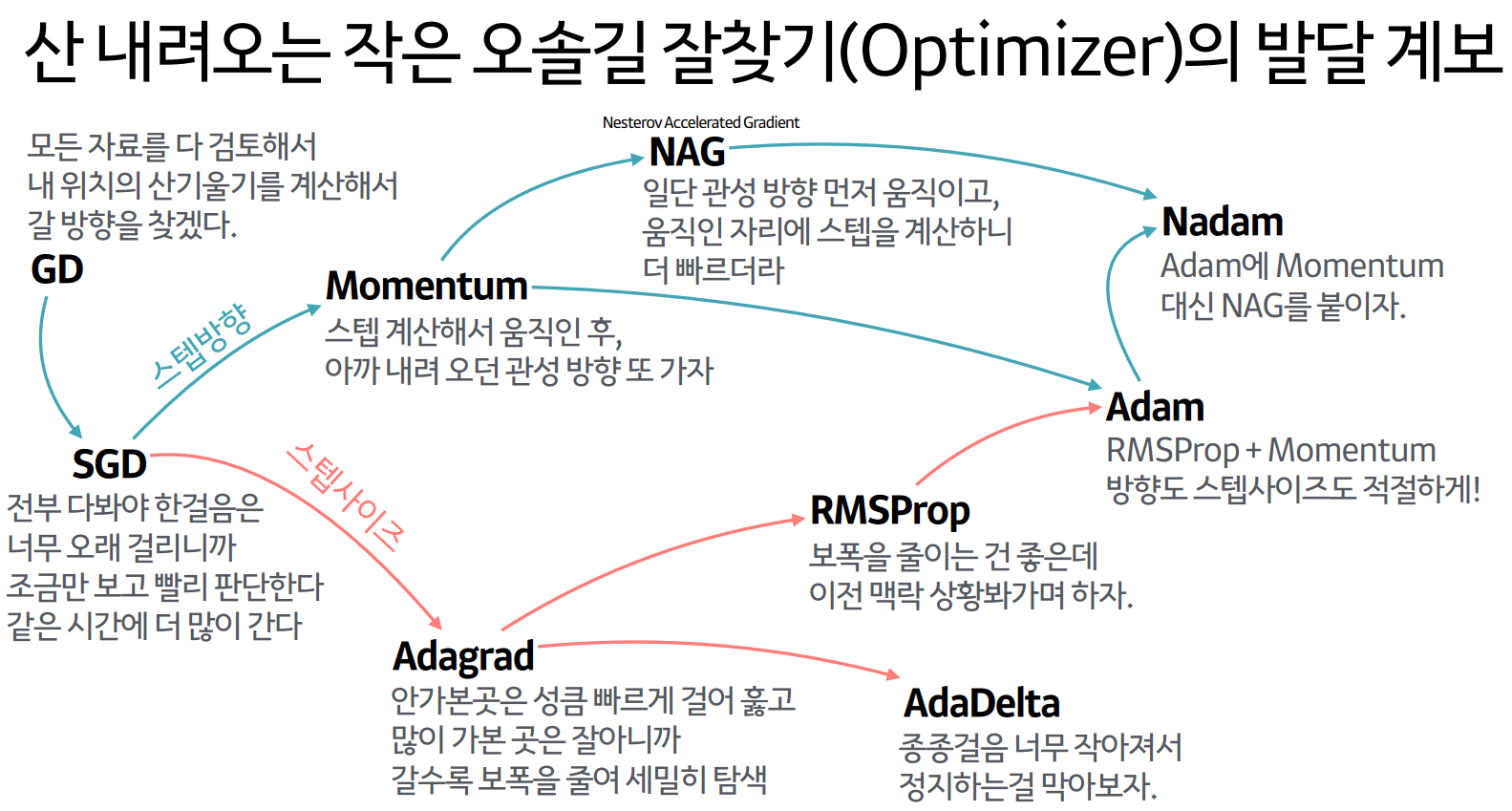
SGD의 단점을 개선하는 방법 - 방향 중심
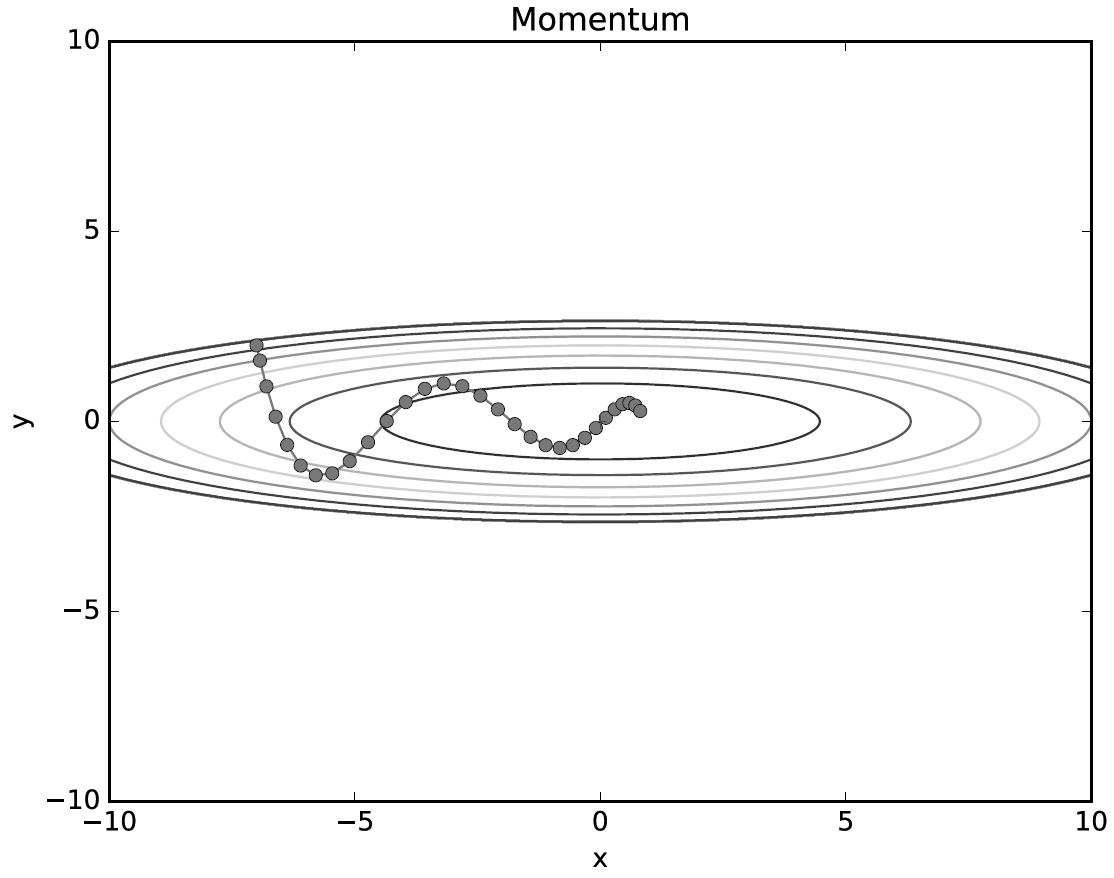
모멘텀
class Momentum: def __init__(self, lr = 0.01, momentum = 0.9): self.lr = lr self.momentum = momentum self.v = None def update(self, params, grads): if self.v is None: self.v = {} for key, val in params.items(): self.v[key] = np.zeros_list(val) for key in params.keys(): self.v[key] = self.momentum * self.v[key] - self.lr * self.grads[key] self.params[key] += self.v[key]
적용 결과
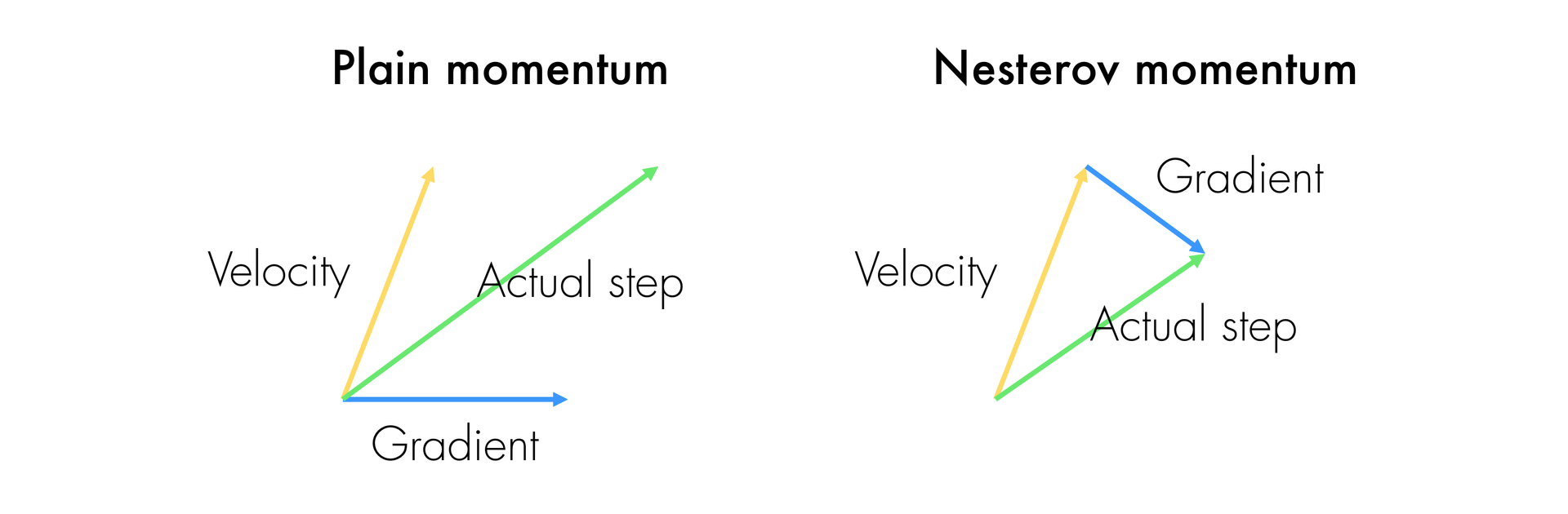
Nesterov Momentum(NAG)
SGD의 단점을 개선하는 방법 - 보폭 중심
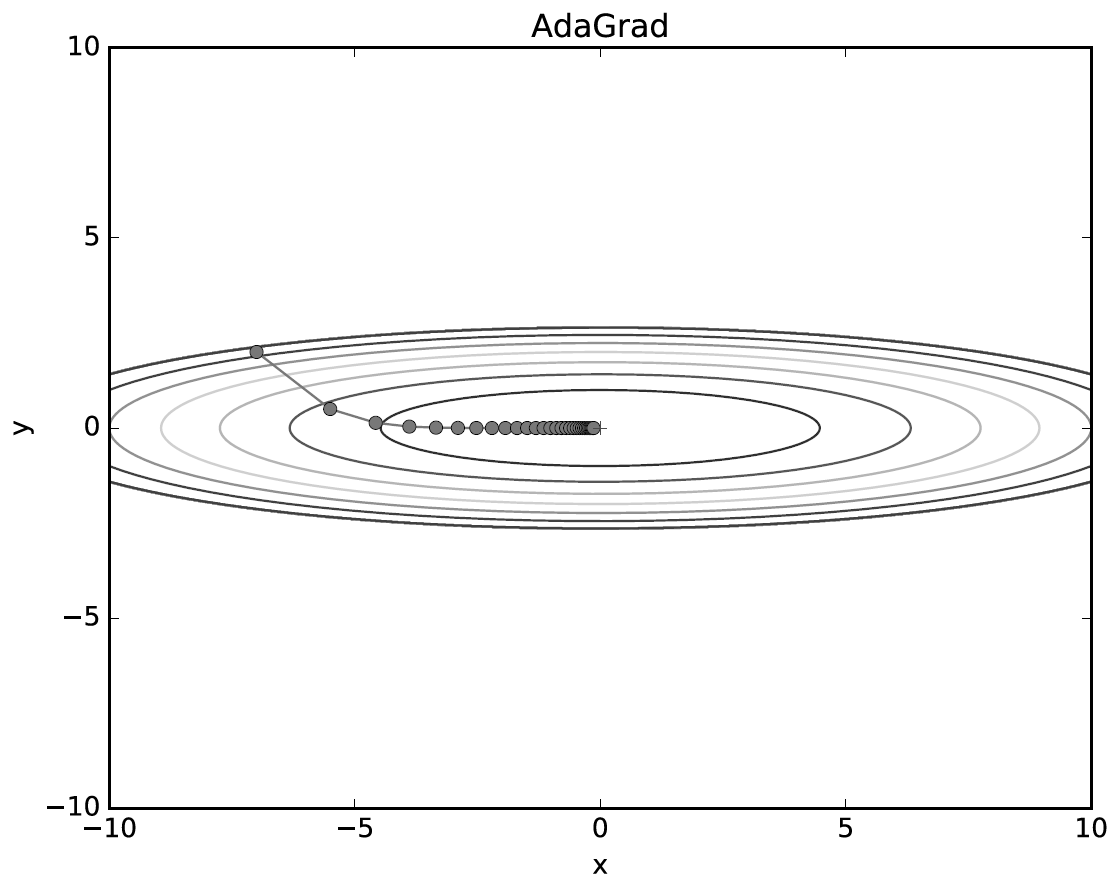
AdaGrad
class AdaGrad: def __init__(self, lr = 0.01): self.lr = lr self.h = None def update(self, params, grads): if self.h is None: self.h = {} for key, val in params.items(): self.h[key] = np.zeros_like(val) for key in params.keys(): self.h[key] += grads[key] * grads[key] params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
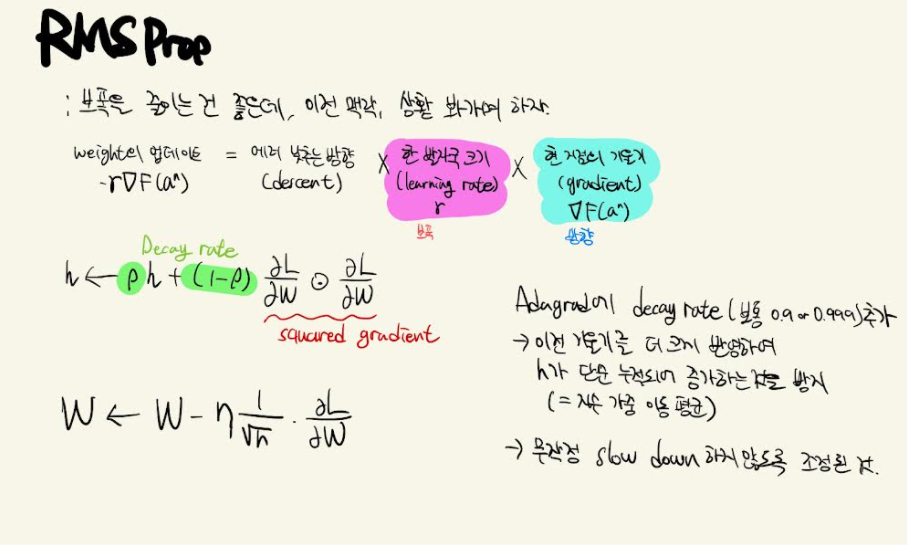
RMSProp
def rmsprop(f, gfx, x, ir=100, h=np.array([0.1, 0.1]), gamma=0.001, lamb=0.1, rho = 0.5, th=0.00001): h = h.copy() log = np.array([]) for i in range(ir): log = np.append(log, x) gx = gfx(x) h = rho*h + (1 - rho)*gx**2 xNew = x-lamb*gx/(h**(1/2)) if(sum(abs(x-xNew)) <th): break x = xNew log = log.reshape(len(log)//2, 2) return x, i, log x = np.array([0,0]) xm, _, log = rmsprop(fx, gfx, x, rho=0.8,ir=1000) plotLog(log)
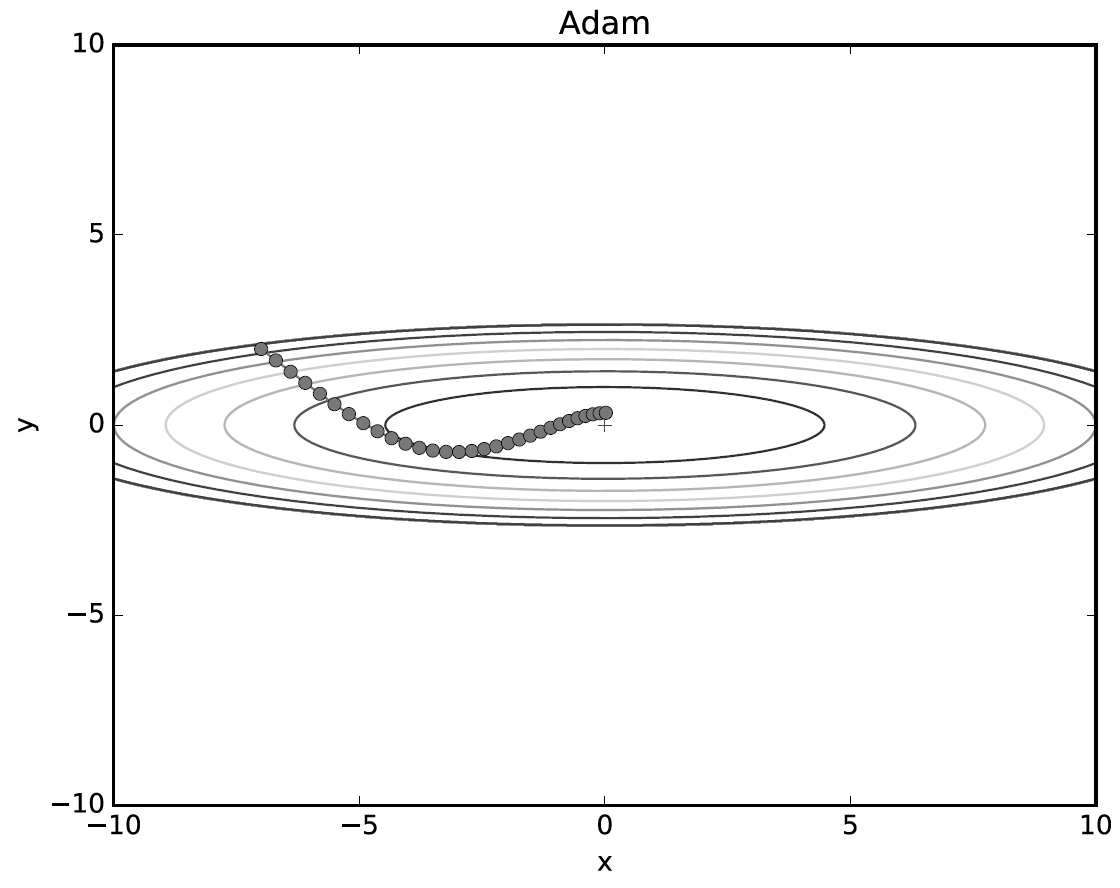
Adam
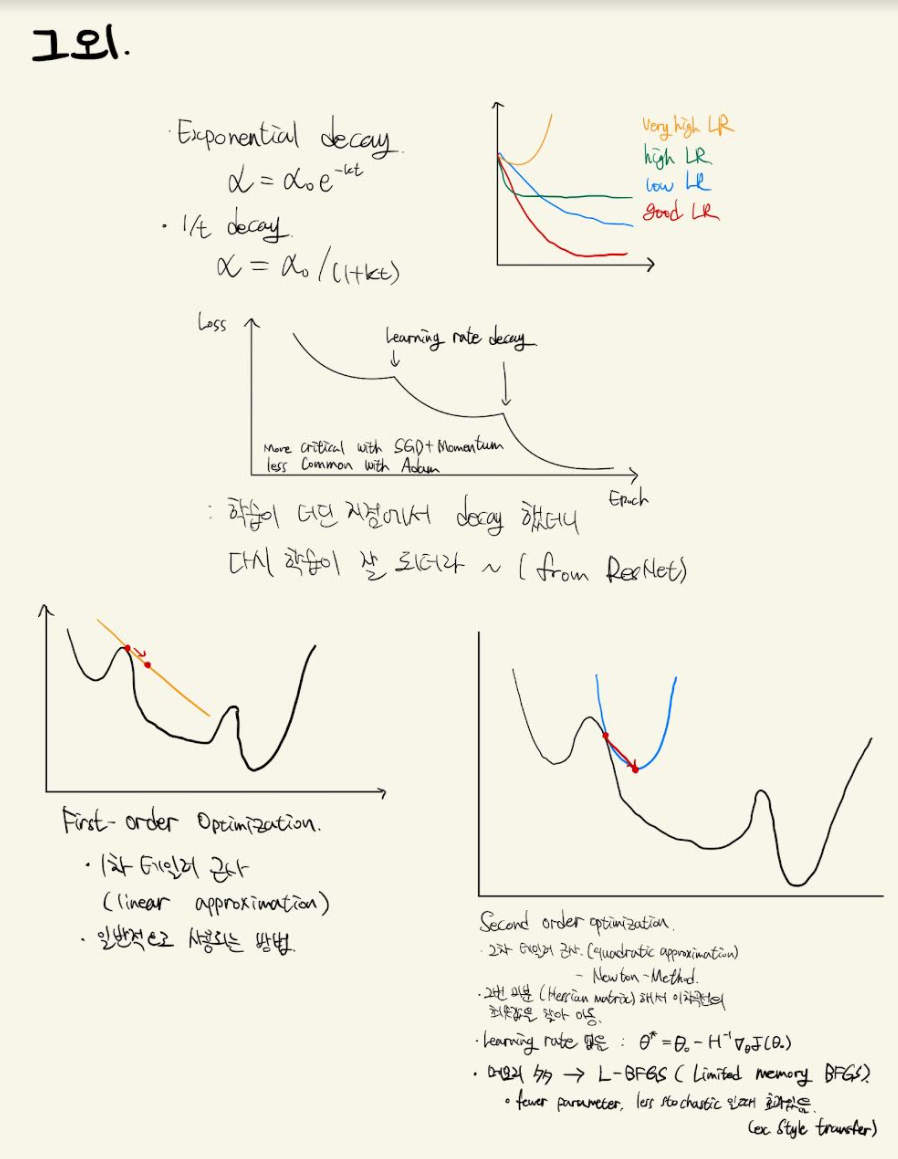
- 그 외
2. Regularization
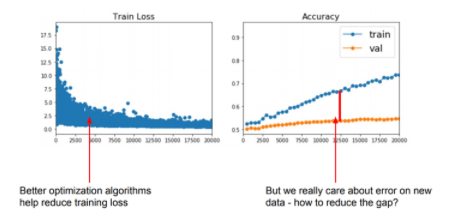
- Optimization이 training error를 줄이는데 집중했다면, 이제는 valid error와의 차이를 줄여 과적합(overfitting)을 방지할 차례
- 과적합을 줄이면서 valid accuracy를 최대로 끌어올린다.
1) Model Ensemble
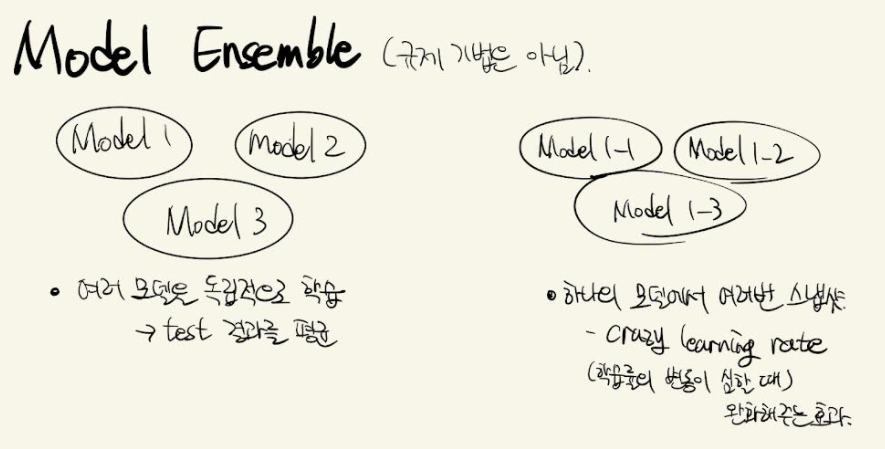
2) L1, L2 Regularization

3) Dropout

4) Data Augmentation
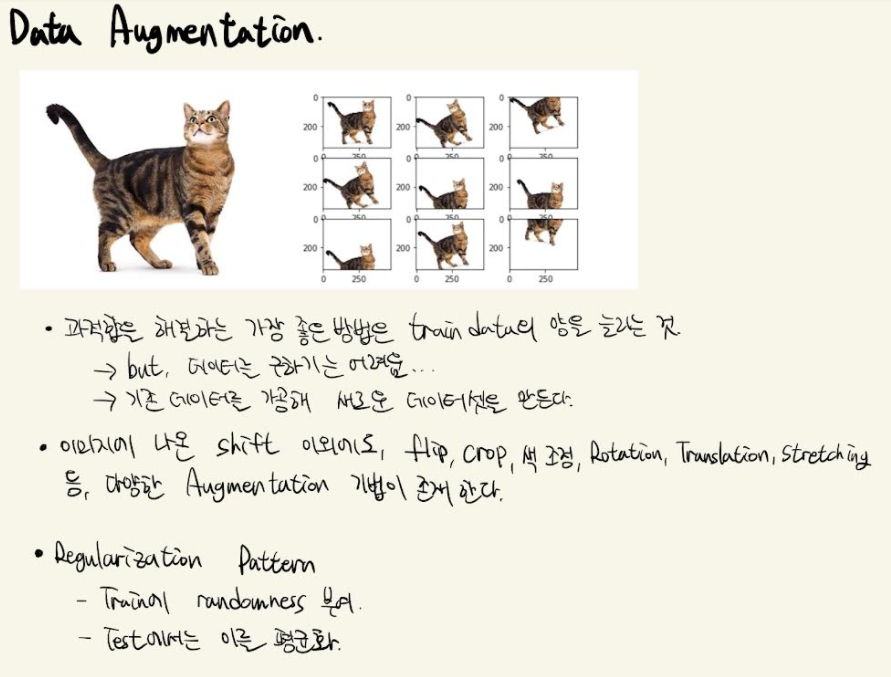
5) 그 외

3. Transfer learning