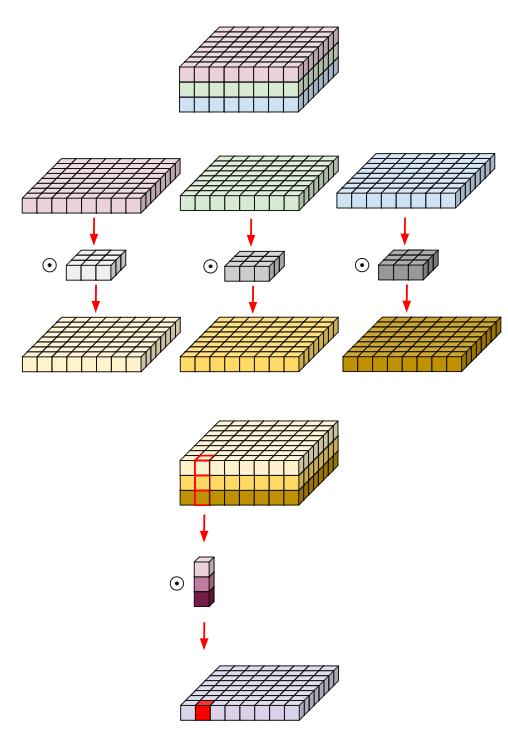
1. Convolution 연산의 성질

(1) 파라미터 공유(Parameter sharing)

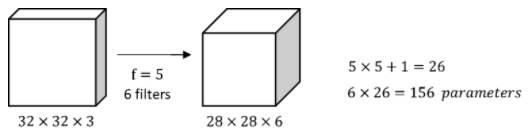
• parameter의 개수 = ((5 5 3) + 1) * 6 = 456개
  
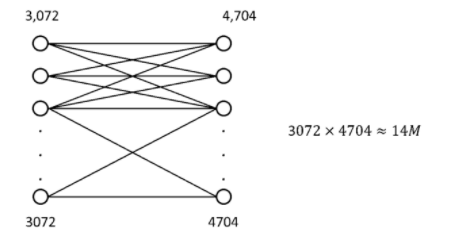
• Fully connect 할 경우 약 1400만개의 파라미터가 필요
  

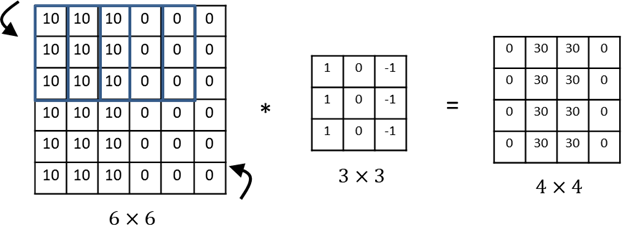
• vertical edge detector( 세로 윤곽선 검출 )
• 하나의 필터만으로 6*6크기의 이미지 전체에서 윤곽선을 찾아낼 수 있다.

(2) 희소 연결(Sparsity of connections)

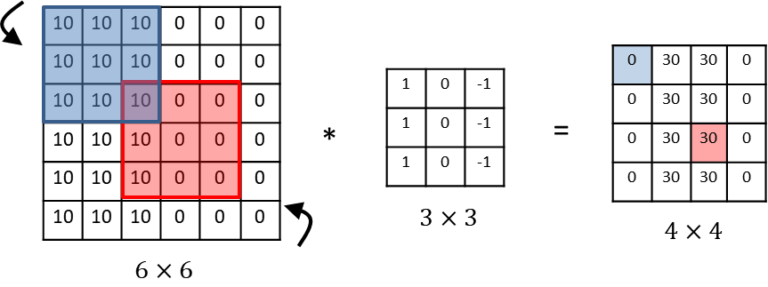
• 출력값이 이미지의 일부에만 영향을 받고 나머지 픽셀들에는 영향을 받지 않는다.

→ CNN의 변수공유와 희소연결이라는 특징때문에 신경망 변수가 줄어들어 훈련 셋이 작아지고, 과대적합도 방지할 수 있다.

(3) 이동 등변성(= 이동 불변성, translation equivariance, translation invariance)

몇 픽셀 이동한 이미지도 유사한 속성을 가지게 하고, 입력 이미지의 모든 위치에 동일한 필터를 적용해 신경망이 자동적으로 학습하고 이동 불변성을 포착할 수 있다.

즉, 이미지가 약간의 변형이 있어도 이를 포착할 수 있다는 것이다.

• 예시

1) Max Pooling

• 대표적인 small translation invariance 함수
• 예시
  • Original image = [1, 0, 0, 0]
  • Translated image = [0, 0, 0, 1] , [0, 1, 0, 0]
  • 2x2 Maxpooling을 할 경우 모두 동일하게 1이라는 output을 출력한다.
• k x k 범위 내에서의 translation에 대해서는 invariance하다.

2. 개선된 컨볼루션 연산

Convolution 연산의 한계

1. 파라미터 수와 계산량이 많다.
2. 죽은 채널이 발생해도 알기 어렵다.

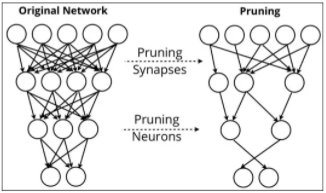
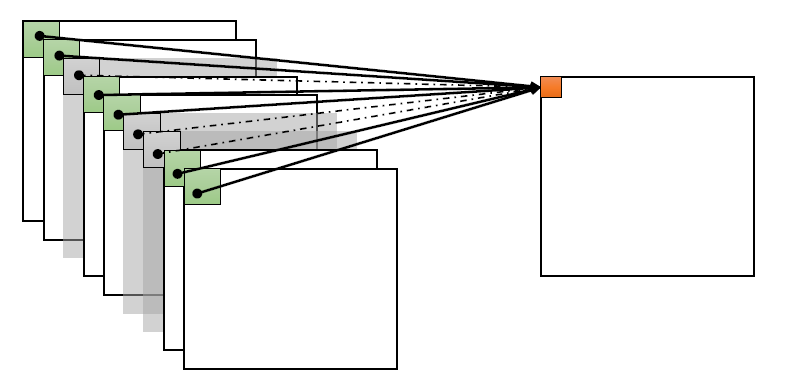
1. 채널 간 낮은 상관관계
   1. 학습 수렴 속도 저하
   2. 일종의 Noise처럼 작용
   3. 불필요한 가중치와 연산의 존재

(1) 팽창 컨볼루션(Dilated Convolution)

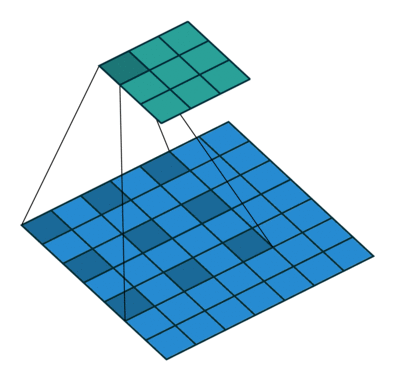
• 영상 내의 Object에 대한 정확한 판단을 위해서는 Contextual Information이 중요하다.

  • Contextual Information?

  • 객체 주변의 배경은 어떤가

  • 객체 주변의 다른 객체들은 어떤 종류인가

    

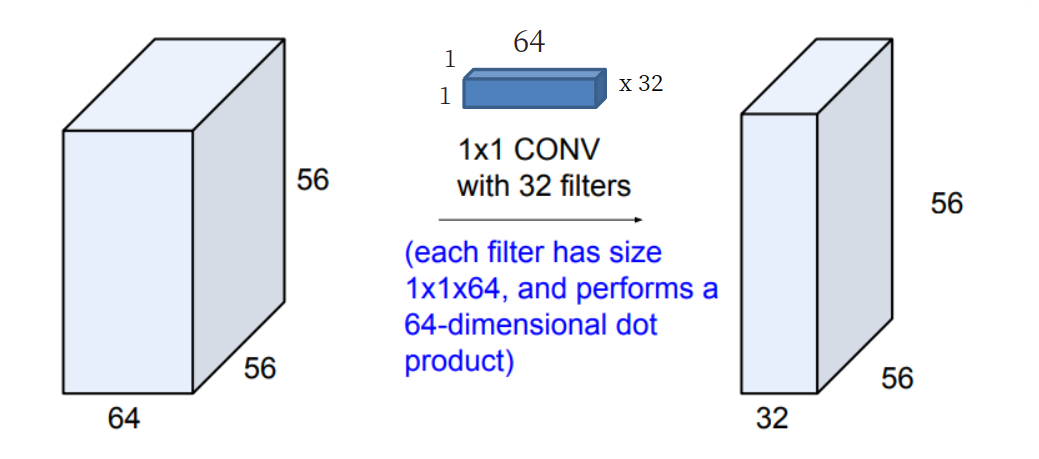
(2) 점별 컨볼루션(Pointwise Convolution)

• Pointwise Convolution?
• 커널의 크기가 1x1로 고정된 Convolution layer

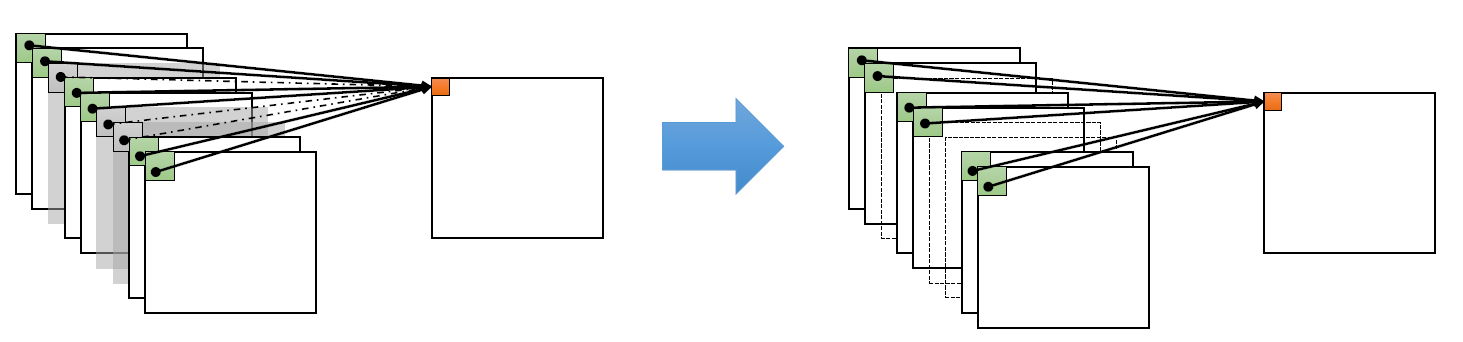
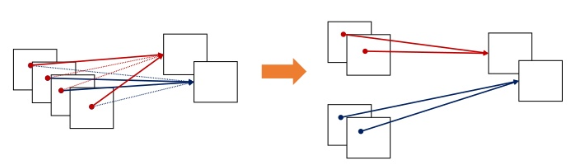
(3) 그룹 컨볼루션(Group Convolution)

• input image의 채널들을 여러 개의 그룹으로 나누어 독립적인 Convolution을 수행하는 방식

def grouped_convolution(input, n_groups):
		input_groups = tf.split(input, n_groups, axis=-1)

		output_groups = [
				tf.layers.conv2d(input_groups[i], """ some params """) for i in range(n_groups)
		]
		
		output = tf.concat(output_groups, axis=-1)
		return output

• 각 그룹의 입력 채널들 사이에 독립적인 필터를 학습한다.

  

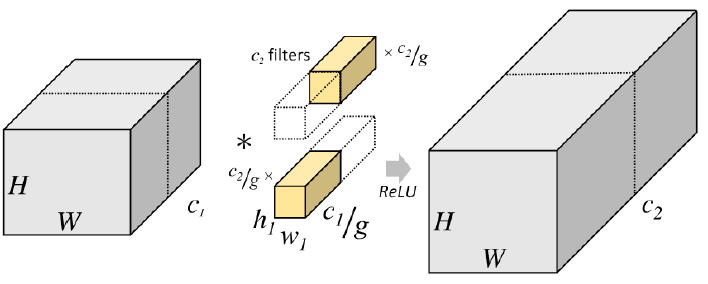
  • 더 낮은 파라미터 수와 연산량
  • 각 그룹에 높은 Correlation을 가지는 채널들이 학습될 수 있다.

• 결과적으로 각 그룹마다 독립적인 필터의 학습을 기대할 수 있다.

  

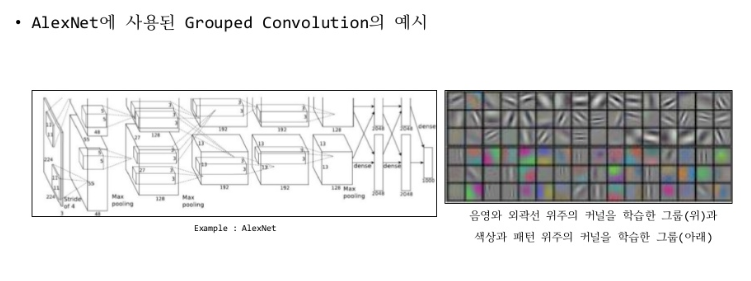
• 특징

  • 그룹 수를 조정해 독립적인 필터 그룹을 조정할 수 있다.

  • 그룹의 수는 hyper parameter라는 단점이 있다.

  • 병렬처리에 유리하다.

    

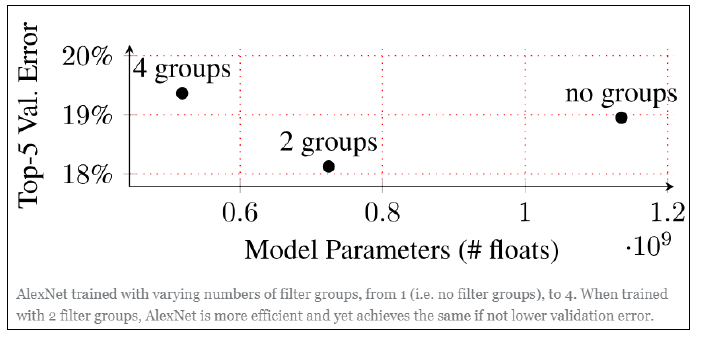
(4) 깊이별 컨볼루션(Depthwise Convolution)

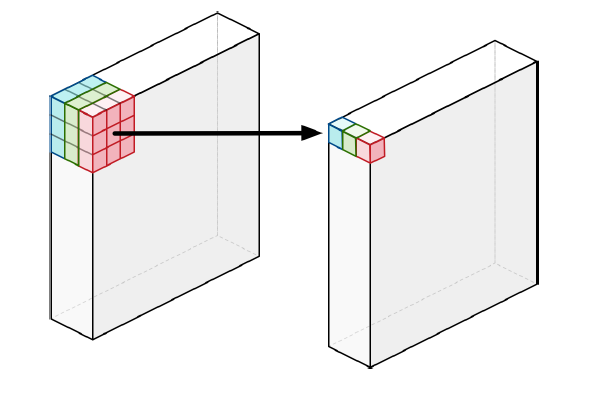
• 각 단일 채널에 대해서만 수행되는 필터들을 사용
• 컨볼루션을 수행하면 필터 별 spatial feature만을 뽑아낼 수 있다.
• 그룹 컨볼루션의 채널 수가 1개이면 깊이별 컨볼루션과 같다.

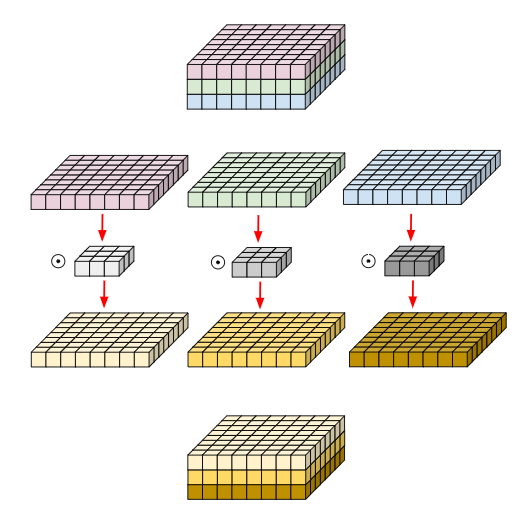
• 883 matrix 깊이별 컨볼루션 수행

(5) 깊이별 분리 컨볼루션(Depthwise Seperable Convolution)

• 기존의 Convolution에서 채널 간 상관관계를 완벽히 분리하기 위한 구조
• 깊이별 컨볼루션(Depthwise Convolution)과 점별 컨볼루션(Pointwise Convolution)을 조합해 사용하는 방식

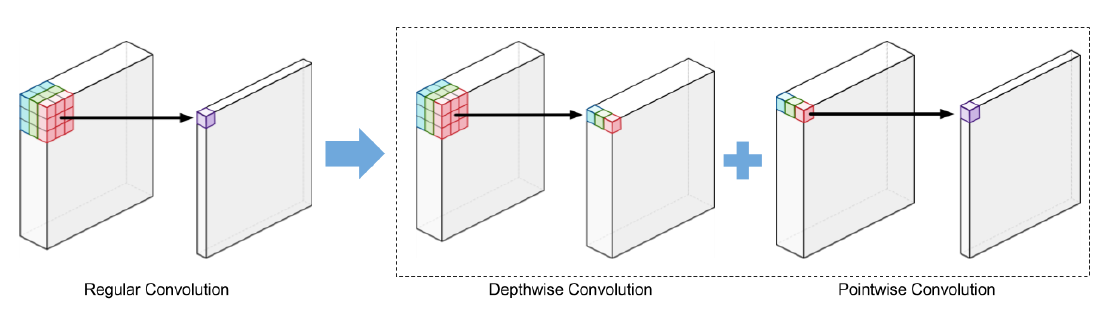
• 기존 Depthwise Convolution을 진행한 결과물에 각 채널을 1개의 채널로 압축할 수 있는 추가적인 Convolution을 진행하여 결과물이 간략하게 나오도록 하는 과정