1. Norm
Norm은 벡터의 크기(길이)를 측정하는 방법(함수)이다. 즉, 두 벡터 사이의 거리를 측정하는 방법이다.
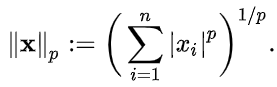
- 위 식에서 p는 Norm의 차수를 의미한다. p=1 이면 L1 Norm이고, p=2 이면 L2 Norm이다.
- n은 해당 벡터의 원소 수이다.
즉, Norm이라는 것은 벡터가 됐든, 값이 됐든 어떠한 값들의 크기를 계산해 비교할 수 있는 수치로 만드는 함수라고 볼 수 있다.
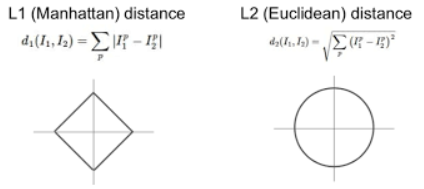
(1) L1 Norm(Manhattan Distance, Taxicab geometry)
그림 2에서 볼 수 있듯이, L1 Norm은 두 벡터의 차에 절대값을 취한 후 모두 합한 값이다.
x = (1, 3, 2) , y = (4, -1, 5) 일 때
-> d(x, y) = |4-1| + |-1-3| + |5-2| = 10 이다.(2) L2 Norm(Euclidean Distance)
수학적으로 '거리'를 말할 때 가장 기본적으로 사용되는 Euclidean 거리를 의미한다. 일반적으로 거리를 측정할 때 그러하듯 각 원소값의 차의 제곱을 합한 후에 루트를 씌운 값이다.
x = (1, 3, 2), y = (4, -1, 5) 일 때
-> d(x,y) = √((4-1)² + (-1-3)² + (5-2)²) = √34 이다.(3) L1 Norm과 L2 Norm의 직관적 차이
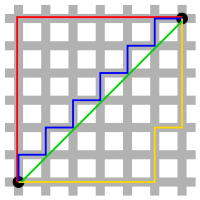
그림 3을 보면, 두 개의 검은 점(벡터)를 잇는 여러 선들이 존재한다. L1 Norm은 빨간색, 파란색, 노란색을 포함해 무수히 많은 Shortest Path를 갖는다. 하지만 L2 Norm은 오직 초록색의 Unique Shortest Path를 갖는다.
Loss
(1) L1 Loss
이러한 Norm이라는 개념을 통해 예측값과 실제값의 차이 즉, Loss를 계산할 수 있다. L1 Loss는 그림 2에서 볼 수 있는 첫 번째 수식의 I_1과 I_2를 각각 y_true와 y_predicted로 대체한 것이다.
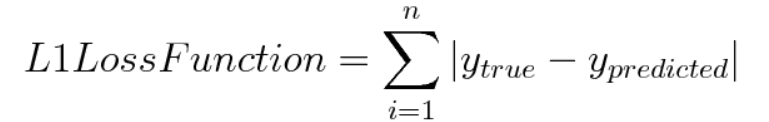
(2) L2 Loss
L2 Loss 역시 그림 2의 L2 Norm에 대한 수식에 y_true와 y_predicted를 대입한것이다. 다만 다른점이 있다면, L2 Loss에는 루트를 취하지 않는다는 점이다.
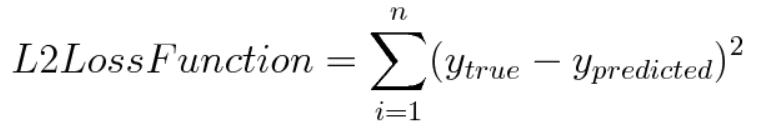
(3) L1 Loss와 L2 Loss의 특성
| L1 Loss | L2 Loss |
|---|---|
| Robust | Not very robust |
| Unstable solution | Stable solution |
| Possibly multiple solution | Always one solution |
- Robust : 이상치에 영향을 덜 받는다는 의미이다. 예를 들어 L2 Loss의 경우 이상치가 있다면 예측값과 실제값 사이의 차이를 제곱하기 때문에 실제보다 더욱 큰 Loss값을 가질 것이다.
- Stablility : 모델이 비슷한 데이터에 대해 얼마나 일관적인 예측을 할 수 있는지를 의미한다.
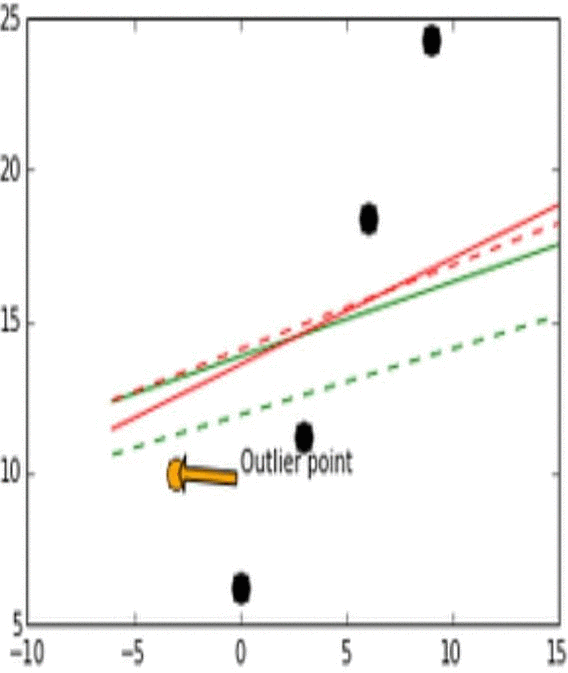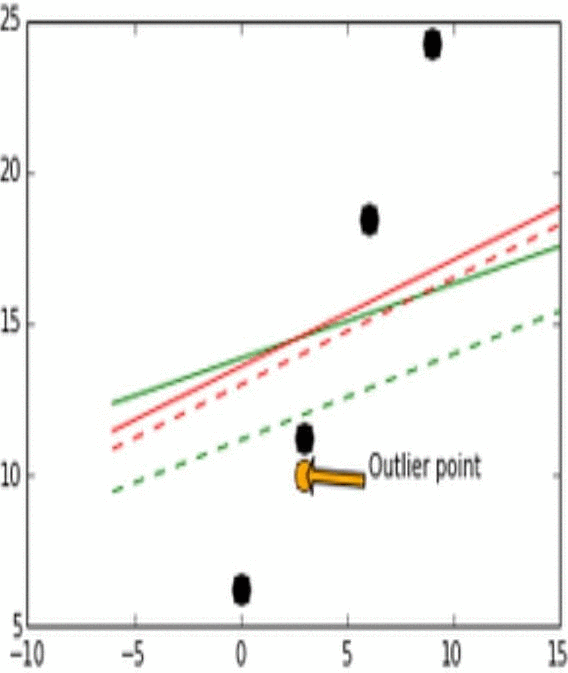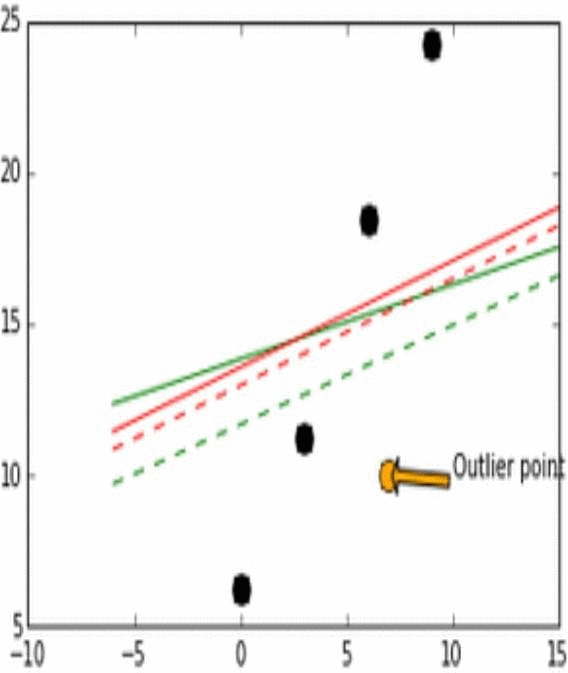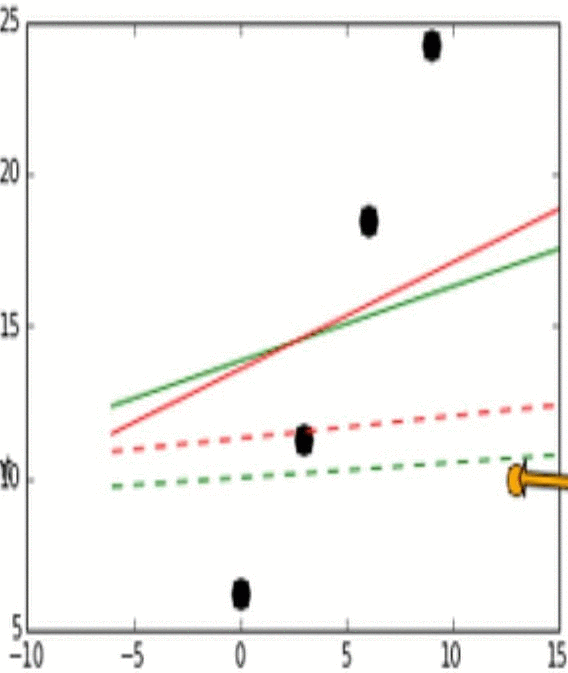 그림 6
그림 6
| 검은 점 | 실제 데이터 |
| 주황 점 | Outlier Point, 이상 데이터 |
| 빨간 실선 | L2 Loss |
| 빨간 점선 | 이상데이터 변화에 따른 L2 Loss의 변화 |
| 초록 실선 | L1 Loss |
| 초록 점선 | 이상데이터 변화에 따른 L1 Loss의 변화 |
그림 6에서 확인할 수 있듯이, 이상치가 실제값에 가까울 때는 L2 Loss 그래프는 변화가 없으나 L1 Loss 그래프는 이상치가 어떤 값을 갖건 다양한 변화가 있다. 이러한 특성으로 인해 L1이 unstable하고, L2가 stable하다고 할 수 있다.
3. Regularization
Regularization은 보통 '정규화'라고 번역되지만, 이는 Normalization과 헷갈릴 수 있고, 실질적으로 Overfitting을 예방하고 Generalization(일반화) 성능을 높이는 데 도움을 준다. 실질적으로 '일반화'라고 번역을 하는 것이 더 적합하다고 볼 수 있다.
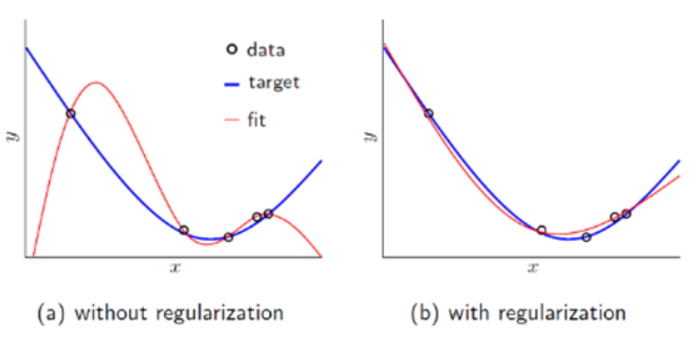
그림 7과 같이 일반적으로 데이터를 통해 모델을 학습할 때 Cost Function이 가장 작아지는 방향으로 학습을 진행하게 된다. 하지만 이는 특정 가중치 값들이 커지면서 Overfitting을 발생시켜 결과를 더 나쁘게 만들 수 있다. 이 때, 정규화 요소(Regularization Term)을 Cost Function에 더해 특정 파라미터가 과도하게 커지지 않고, 모델을 조금 더 General하게 만들 수 있다.
(1) L1 Regularization(Lasso Model)
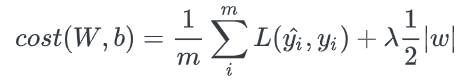
그림 8의 수식에서 앞부분은 Loss(Cost) Function이다. 결국 Loss Function에 L1 정규화 요소(Regularization Term)을 더해 기존 Loss에 절대값만큼의 패널티를 줌으로써 Overfitting을 방지한다.
기본적으로 Loss Function은 그 값이 작아지는 방향으로 학습된다. 하지만 무조건적으로 Loss만을 줄인다면 Overfitting이 발생하게 되므로, 가중치의 절대값(L1 Regularization Term)을 더해 Loss Function을 통해 학습되는 정도를 상쇄시키는 역할을 하는 것이다.
(2) L2 Regularization(Ridge Model)
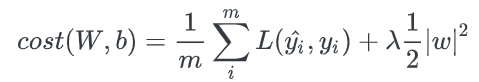
그림 9의 수식에서 알 수 있듯이, L1 Regularization과 L2 Regularization의 차이는 Regularization Term이 절대값을 더해주는지, 제곱을 더해주는지의 차이이다.
(3) L1 Reg와 L2 Reg의 차이와 선택기준
-
λ는 learning rate(학습률) 같은 상수로, 정규화를 어느 정도로 반영할 것인지를 정하는 상수이다.
-
Regularization은 결국 가중치 W가 작아지도록 학습하는 것이고, 이는 결국 Local Noise에 영향을 덜 받겠다 = Outlier의 영향을 더 적게 받겠다는 의미이다.
-
L1 Reg는 통상적으로 상수 값을 빼주도록 되어 있기 때문에 작은 가중치들은 거의 0으로 수렴되어 몇개의 중요한 가중치들만 남게 된다.
-
즉, Feature Selection이 가능해 Sparse Model을 학습시키는데 적합하다.
-
그에 반해 L2 Reg는 이상치에 대응하는 가중치를 0에 가깝게 만들 뿐 0으로 만들지는 않는다.
-
L1 Reg처럼 이상치에 대해 아예 영향을 받지 않게는 못하지만 항상 일반화 성능을 향상시킬수 있다. (Robust하지 않고, Stable한 Solution을 늘 제공한다.)