인덱스 구조
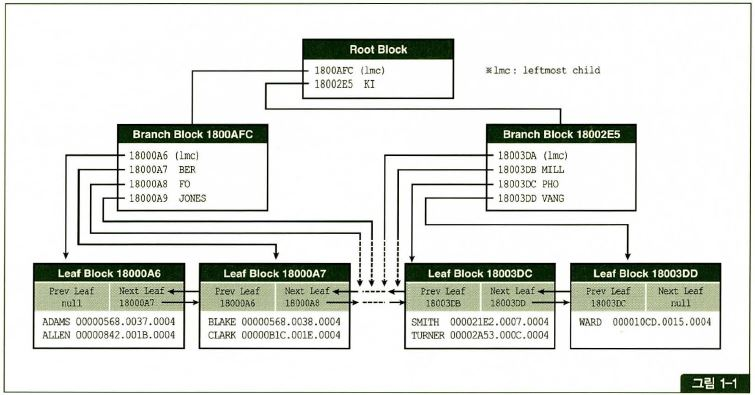
인덱스
-
인덱스(Index)는 색인이라고도 불리며 그 역할은 검색속도를 향상시키는 데 있습니다.
-
여기서 검색은
SELECT명령 및WHERE구를 통해 조건을 지정하여 그에 알맞는 행을 찾는 과정을 의미합니다. -
테이블에 인덱스가 존재하면 효율적인 검색이 가능해져
WHERE구로 조건이 지정된SELECT명령의 처리 속도가 향상됩니다. -
예를 들어 목차를 생각하면 편합니다.
-
백과사전에 목차가 존재하지 않으면 과일이라는 단어를 찾을 때 앞에서부터 하나씩 다 살펴봐야 합니다.
-
그러나 목차가 존재하면 해당 목차를 통해 과가 일치하는 곳으로 바로 가서 훨씬 효율적으로 찾을 수 있습니다.
인덱스 또한 이처럼 검색에 사용되는 키워드와 대응하는 행의 장소가 저장되어 있습니다.
- 이때 인덱스는 테이블과는 별개로 독립된 데이터베이스 객체로 작성됩니다.
- 그러나 인덱스는 결국 테이블에 종속되어 있기 때문에 테이블이 없으면 아무런 의미가 없어 테이블이 삭제될 때 함께 삭제됩니다.
검색에 사용하는 알고리즘
- 데이터베이스의 인덱스에 쓰이는 대표적인 검색 알고리즘은
이진 트리(Binary Tree)를 활용한 이진 검색(Binary Serach) 또는 해시(Hash)가 있습니다.
풀 테이블 스캔(Full Table Scan)
인덱스가 지정되지 않은 테이블을 검색할 때는 풀 테이블 스캔(Full Table Scan)이라 불리는 검색 방법을 사용합니다.
- 이는 말 그대로 테이블에 저장된 모든 값을 처음부터 차례로 조사해나갑니다.
- 매우 단순한 방법으로 만약 행이 100개가 존재한다면 값을 최대 100번 비교합니다.
이진 탐색(Binary Search)
이진 탐색(Binary Search)은 집합을 반으로 나누어 조사하는 방법으로 차례로 나열된 집합에 대해 유효한 검색 방법입니다.
- 아래와 같이 나열된 집합에서 30을 찾는다고 가정해봅시다.
- 이진 탐색은 해당 집합의 가운데 값인 20에 접근하여 검색하고자 하는 숫자(30)가 이보다 작다면 좌측 절반을, 크다면 우측 절반을 조사하고 또한 다시 해당 절반의 중간을 잡아 이 절차를 반복합니다.
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
| 1 | 2 | 3 | 5 | 10 | 11 | 19 | 20 | 23 | 30 | 31 | 32 | 38 | 40 | 100 |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-
이런 방식을 사용하면 결국 집합의 개수 또는 길이만큼 반복해야 했던 풀 테이블 스캔과 비교하여 이진 탐색은 선형 로그 시간이 걸립니다.
-
선형 로그 시간은 자료구조의 복잡도(Complexity)에서 등장하는 개념입니다. 어떤 행위를 수행하기 위해 걸리는 시간과 공간을 수치화하는 표현이라 생각하면 편합니다.
이진 트리(Binary Tree)
- 이진 탐색은 고속으로 검색이 가능하지만 데이터가 미리 정렬되어 있어야 하는 단점이 있습니다.
- 테이블 내의 모든 행을 언제나 정렬된 상태로 두는 것은 어렵기 때문에 이럴 때 테이블 데이터와 별개로 인덱스용 데이터를 저장장치에 만듭니다.
- 이때 사용하는 자료구조가 바로 이진 트리(Binary Tree)입니다.
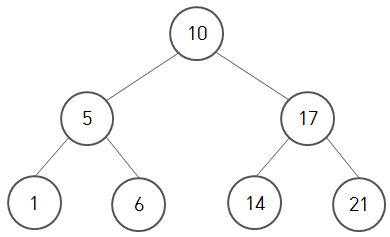
위 이진 탐색의 집합 예시를 이진 트리로 표현하면 아래와 같습니다.
-
트리는 노드(Node)라는 요소로 구성됩니다.
-
그리고 각 노드는 두 개의 가지(Branch)로 나뉩니다.
-
이때 두 가지를 비교했을 때 좌측 가지에는 더 작은 값이, 우측에는 더 큰 값이 놓입니다.
-
이처럼 두 개의 가지로 분기하는 구조라서 이진 트리라 부릅니다.
-
검색은 이러한 이진 트리의 가지를 통해서 행해집니다.
-
맨 위 10이라는 루트 노드(Root Node)를 시작으로 이진 탐색과 비슷한 방식을 사용하여 원하는 수치와 비교해 더 작으면 왼쪽 가지를, 더 크면 오른쪽 가지를 선택해 조사해 나갑니다.
유일성
- 이진 트리에서는 동일한 값을 가진 노드가 존재할 수 없습니다.
- 따라서 무조건적으로 대소비교가 가능하여 가지가 두 개 생성됩니다.
이러한 유일성을 위해 결국 데이터베이스 또한 기본키 제약을 통하여 유일한 값을 가지게 해야 합니다.
