자료구조가 왜 중요할까? 🤔

프로그래머라면 누구나 한 번쯤 듣는 말이 있습니다.

"자료구조를 잘 이해하면, 더 좋은 코드를 짤 수 있다!"

하지만 정작 자료구조를 배울 때는 머리가 아파지곤 하죠. 스택, 큐, 연결 리스트, 트리, 그래프… 😵‍💫

도대체 자료구조가 뭐길래 이렇게 중요한 걸까요? 오늘은 자료구조의 중요성을 10배 더 깊이 있게 파헤쳐 보겠습니다!

---

📌 1. 자료구조는 데이터의 "정리 방법"이다!

자료구조란 무엇인가?

자료구조(Data Structure)는 데이터를 효율적으로 저장하고 관리하는 방법을 의미합니다. 컴퓨터는 데이터를 처리하는 기계이므로, 데이터를 어떻게 정리하느냐에 따라 성능과 효율성이 크게 달라집니다. 자료구조는 데이터를 조직화하고, 접근 및 수정하는 방법을 체계화하여 프로그램의 성능을 최적화하는 데 필수적입니다.

왜 자료구조가 중요한가?

• 효율성: 잘 설계된 자료구조는 데이터의 검색, 삽입, 삭제 등의 연산을 빠르게 수행할 수 있게 해줍니다.
• 가독성 및 유지보수성: 적절한 자료구조를 사용하면 코드가 더 명확해지고, 유지보수가 쉬워집니다.
• 확장성: 자료구조를 이해하면 복잡한 시스템을 설계하고 확장할 때 유리합니다.
• 문제 해결 능력 향상: 다양한 자료구조를 알고 있으면 문제를 더 효율적으로 해결할 수 있습니다.

기본 자료구조의 종류와 예시

📦 배열(Array):

• 설명: 동일한 타입의 데이터를 연속된 메모리 공간에 저장.
• 특징: 인덱스를 통한 빠른 접근(O(1)), 고정된 크기.
• 예시: 책장 – 책을 일렬로 정리하여 원하는 책을 빠르게 찾을 수 있음.

🗄️ 스택(Stack):

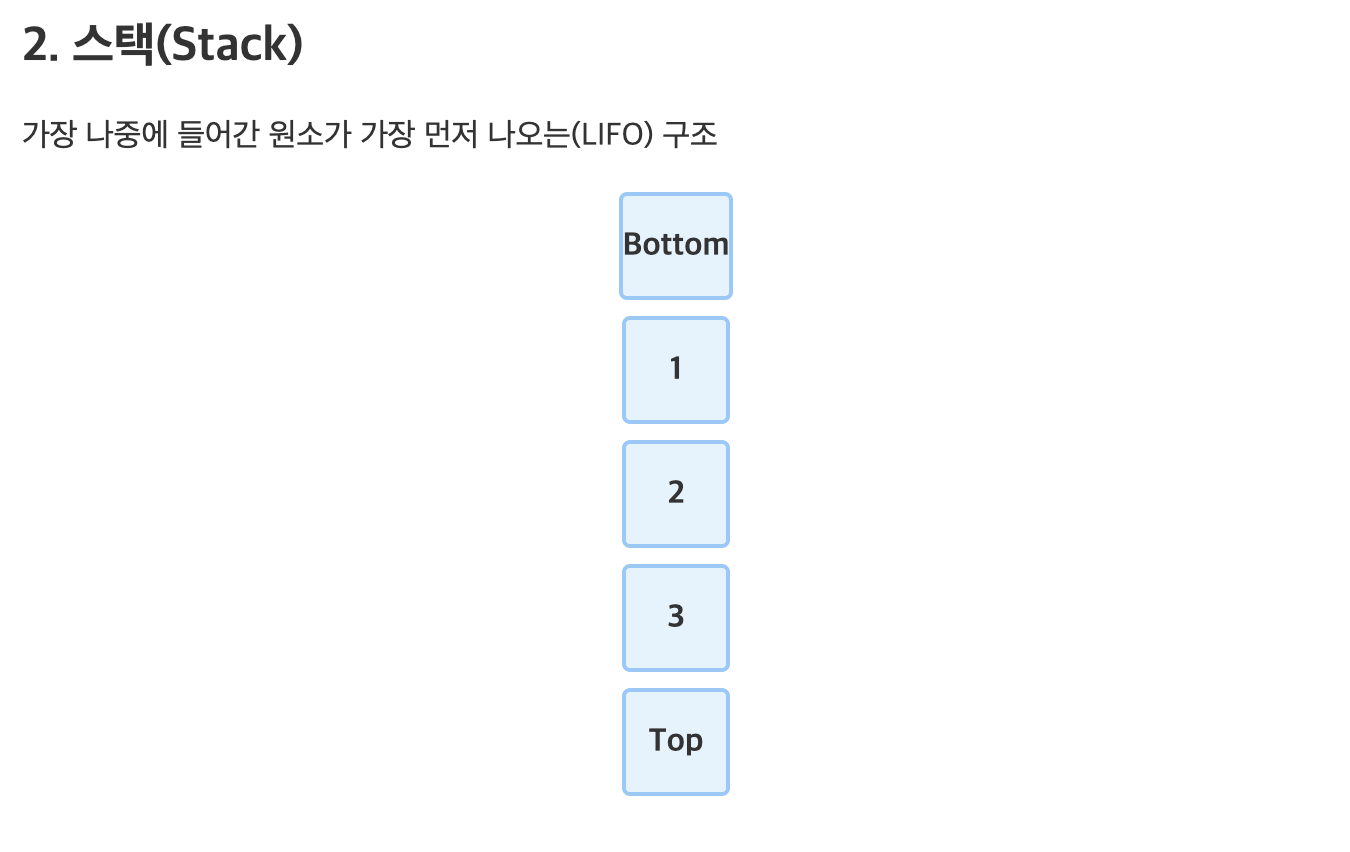
• 설명: 후입선출(LIFO) 방식으로 데이터를 관리.
• 특징: 마지막에 추가된 데이터가 먼저 제거됨.
• 예시: 접시 더미 – 가장 위에 있는 접시부터 꺼냄.

🚶‍♂️ 큐(Queue):

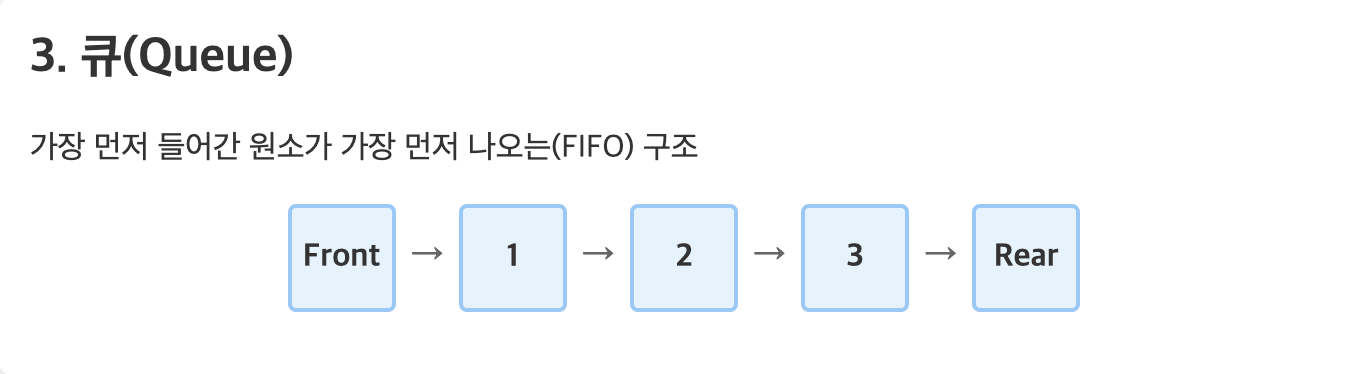
• 설명: 선입선출(FIFO) 방식으로 데이터를 관리.
• 특징: 먼저 추가된 데이터가 먼저 제거됨.
• 예시: 놀이공원 대기줄 – 먼저 온 사람이 먼저 입장.

🔗 연결 리스트(Linked List):

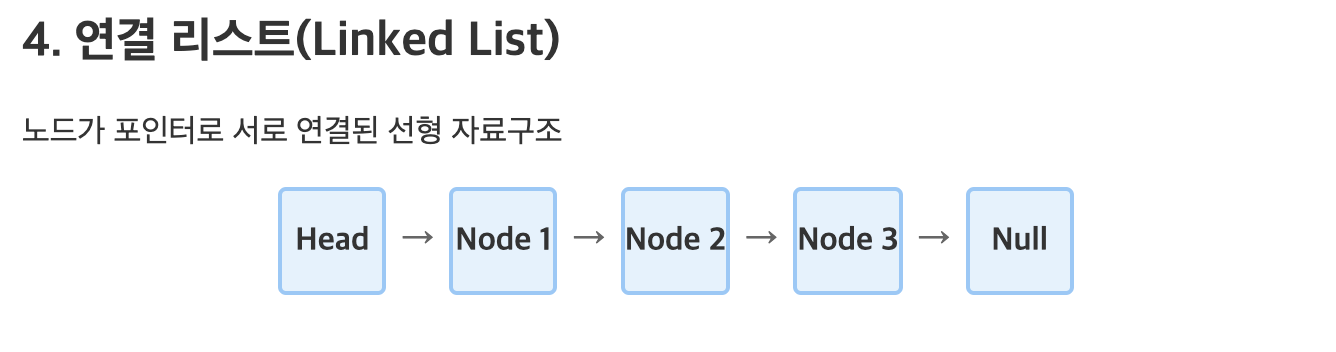
• 설명: 각 노드가 데이터와 다음 노드를 가리키는 포인터를 포함.
• 특징: 동적 크기, 삽입 및 삭제가 용이하지만 임의 접근이 느림.
• 예시: 가족 관계도 – 부모-자식 구조로 쉽게 관계를 파악.

🌳 트리(Tree):

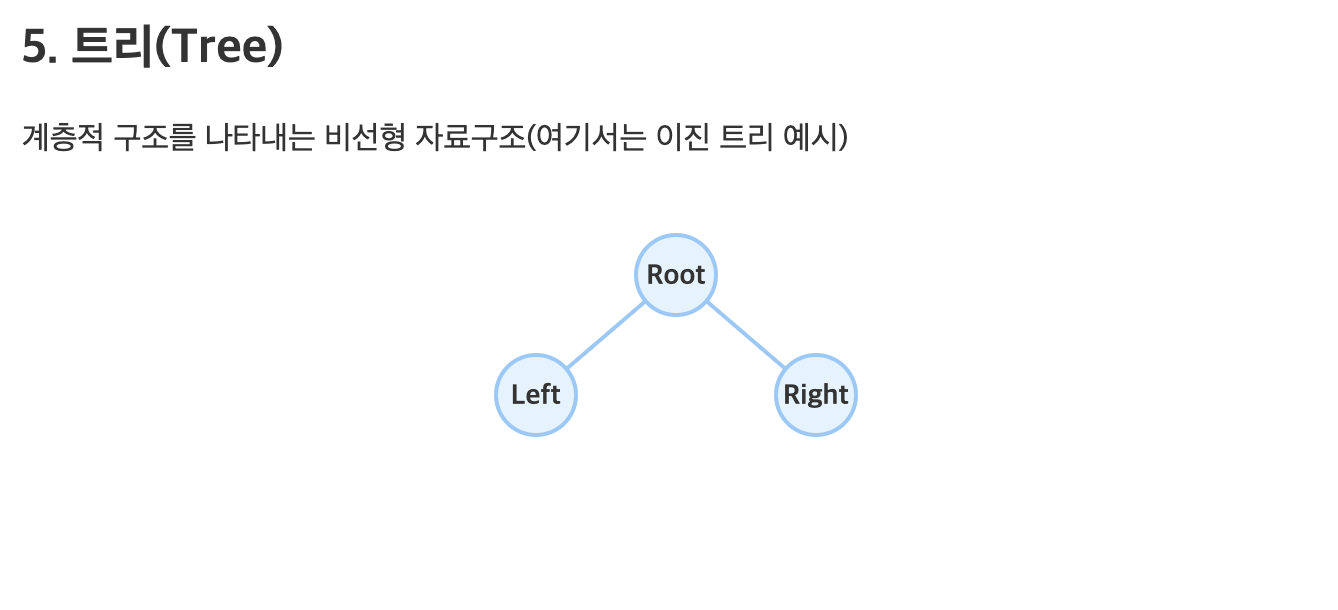
• 설명: 계층적 구조를 가진 자료구조로, 노드 간에 부모-자식 관계가 존재.
• 특징: 빠른 검색과 정렬이 가능, 다양한 종류의 트리가 존재 (이진 트리, AVL 트리, 힙 등).
• 예시: 파일 시스템 – 디렉토리와 파일의 계층적 구조.

🔗 그래프(Graph):

• 설명: 노드(정점)와 노드 간의 연결(간선)으로 구성된 자료구조.
• 특징: 복잡한 관계 표현에 유용, 다양한 탐색 알고리즘 적용 가능 (BFS, DFS 등).
• 예시: 지하철 노선도 – 여러 역이 복잡하게 연결되어 최단 경로를 찾을 수 있음.

자료구조의 시간 복잡도와 공간 복잡도

자료구조를 선택할 때는 시간 복잡도와 공간 복잡도를 고려해야 합니다.

• 시간 복잡도: 연산을 수행하는 데 필요한 시간의 양을 나타냅니다. 예를 들어, 배열의 인덱스 접근은 O(1) 시간이 걸리지만, 연결 리스트에서 특정 위치의 요소를 찾는 데는 O(n) 시간이 걸립니다.
• 공간 복잡도: 자료구조가 사용하는 메모리의 양을 나타냅니다. 예를 들어, 트리는 연결 리스트보다 더 많은 메모리를 사용할 수 있지만, 더 빠른 검색을 제공합니다.

---

🚀 2. 라이브러리를 쓰면 되지 않나? (Yes or No)

📌 2-1. 라이브러리를 활용한 자료구조 정리

위에서 “라이브러리를 쓰는 것도 중요하다!”고 강조했지만, 실제로 어떤 라이브러리를 쓰면 좋을지 감이 안 잡힐 수 있죠. 그래서 자주 쓰이는 Python 라이브러리들을 자료구조별로 간단히 정리해봤습니다.

---

🚀 1) 라이브러리를 사용해야 하는 이유

1. 간편함

   복잡한 자료구조를 처음부터 구현할 필요 없이,

   한두 줄 코드로 바로 사용이 가능합니다.

2. 최적화

   파이썬 표준 라이브러리나 유명 라이브러리는

   이미 성능이 검증되었고, 내부 구현도 깔끔합니다.

3. 유지보수 용이

   내가 직접 구현한 자료구조 코드가 길어질수록

   디버깅과 유지보수가 어려울 수 있지만,

   라이브러리를 사용하면 그런 부분을 신경 쓰지 않아도 됩니다.

---

📚 2) 주요 라이브러리와 자료구조 활용

아래 예시들은 파이썬 기준으로 작성했지만, 다른 언어에도 비슷한 표준 라이브러리나 패키지가 있으니 참고하세요!

📦 배열(Array) 및 리스트(List)

• 라이브러리: Python의 list
• 사용 예시:

  arr = [1, 2, 3, 4]
  arr.append(5)   # 요소 추가
  arr.pop()       # 마지막 요소 제거
  print(arr[2])   # 인덱스 접근(O(1))
  

🗄️ 스택(Stack)

• 라이브러리: Python의 list 또는 collections.deque (파이썬 리스트로도 스택 기능을 충분히 구현 가능)
  
• 사용 예시:

  stack = []
  stack.append(1)  # push
  stack.append(2)
  print(stack.pop())  # pop -> 2
  

🚶‍♂️ 큐(Queue)

• 라이브러리: collections.deque
• 사용 예시:

  from collections import deque
  
  queue = deque()
  queue.append(1)       # enqueue
  queue.append(2)
  print(queue.popleft())  # dequeue -> 1
  

🔗 연결 리스트(Linked List)

• 라이브러리: 파이썬에는 기본 연결 리스트 라이브러리가 없습니다.
• 대체: 일반적인 상황에서는 list로 대부분 대체 가능합니다.
  다만, 정말 연결 리스트가 필요한 경우 직접 구현해야 합니다.

🌳 트리(Tree)

• 라이브러리: anytree (서드파티) 또는 직접 구현
• 사용 예시:

  from anytree import Node, RenderTree
  
  root = Node("Root")
  child1 = Node("Child1", parent=root)
  child2 = Node("Child2", parent=root)
  
  for pre, fill, node in RenderTree(root):
      print(f"{pre}{node.name}")
  

🔗 그래프(Graph)

• 라이브러리: networkx (서드파티)
• 사용 예시:

  import networkx as nx
  
  G = nx.Graph()
  G.add_edge("A", "B")
  G.add_edge("B", "C")
  
  # "A"에서 "C"까지 최단 경로 찾기
  print(list(nx.shortest_path(G, "A", "C")))  # ['A', 'B', 'C']
  

🔍 해시 테이블(Hash Table)

• 라이브러리: Python의 dict
• 사용 예시:

  hash_table = {}
  hash_table["key"] = "value"
  print(hash_table["key"])  # "value"
  

🌾 힙(Heap)

• 라이브러리: heapq
• 사용 예시:

  import heapq
  heap = []
  
  heapq.heappush(heap, 3)
  heapq.heappush(heap, 1)
  heapq.heappush(heap, 2)
  print(heapq.heappop(heap))  # 1 (최소 힙)
  

🧩 트라이(Trie)

• 라이브러리: pygtrie (서드파티)
• 사용 예시:

  import pygtrie
  
  trie = pygtrie.Trie()
  trie["app"] = True
  trie["apple"] = True
  
  print(trie.has_subtrie("app"))   # True (해당 prefix를 가지는 단어가 있음)
  print(trie.has_key("app"))       # True (정확히 "app" 존재)
  

---

✅ 3) 라이브러리를 활용할 때의 한계와 주의점

1. 내부 동작 이해 부족
   • 라이브러리를 쓰면 구현 원리를 모른 채 기능만 사용할 수도 있습니다.
   • 최적화나 디버깅이 필요할 때 곤란해질 수 있습니다.
2. 커스터마이징 제한
   • 특별한 요구사항(예: 연결 리스트 특성을 변형한 구조)이 필요하면 직접 구현해야 합니다.
3. 비효율적 사용 가능성
   • 자료구조 선택이 잘못되거나, 라이브러리 함수를 잘못 사용하면 오히려 성능이 떨어질 수 있습니다.

---

🎯 4) 라이브러리 활용 팁

1. 기본 자료구조 이해 필수
   • 라이브러리를 그냥 쓰기보다는 스택, 큐, 트리, 그래프 등이 어떤 구조로 만들어졌는지 먼저 파악하세요.
   • 그래야 “이 상황에는 어떤 자료구조를 써야 한다”를 빠르게 결정할 수 있습니다.
2. 적재적소 사용
   • 단순 순회가 많은 경우 리스트를 쓰고, 삽입/삭제가 잦으면 deque를 쓰는 식으로,
     상황별로 라이브러리를 적절히 선택하세요.
3. 심화 학습 병행
   • 필요한 경우 직접 구현을 해보며 구조적인 이해를 깊게 하세요.
   • 코딩 테스트나 면접에서는 직접 구현을 요구하는 경우도 많습니다.
4. 라이브러리 문서 적극 활용
   • Python 공식 문서나 networkx 같은 서드파티 문서를 보면, 더 효율적으로 쓸 수 있는 꿀팁들이 많이 있습니다.

라이브러리의 장점과 한계

맞아요! 파이썬 같은 언어에는 list, deque, heapq 같은 자료구조 라이브러리가 이미 준비되어 있습니다. 이러한 라이브러리를 사용하면 기본적인 자료구조를 손쉽게 구현하고 사용할 수 있습니다.

라이브러리 사용의 장점

• 간편함: 이미 최적화된 코드를 사용할 수 있어 개발 속도가 빨라집니다.
• 신뢰성: 검증된 라이브러리를 사용하면 버그가 적고 안정성이 높습니다.
• 유지보수 용이: 라이브러리가 업데이트되면 최신 기능과 최적화를 자동으로 활용할 수 있습니다.

라이브러리 사용의 한계

• 커스터마이징의 어려움: 특정한 요구사항에 맞춰 자료구조를 수정하기 어려울 수 있습니다.
• 내부 동작의 불투명성: 라이브러리가 어떻게 구현되었는지 알기 어려워, 최적의 성능을 발휘하지 못할 수 있습니다.
• 학습의 한계: 직접 구현하지 않으면 자료구조의 내부 동작 방식을 깊이 이해하기 어렵습니다.

직접 구현의 필요성

라이브러리가 모든 문제를 해결해 주지는 않아요. 우리가 직접 자료구조를 만들 줄 모르면, 최적의 방법을 찾기 어려워질 수 있어요. 직접 구현해 보면 자료구조의 내부 동작을 더 깊이 이해할 수 있고, 복잡한 문제를 해결하는 데 필요한 창의적인 접근 방식을 배울 수 있습니다.

직접 구현한 자료구조 예제

📍 스택(Stack)

class Stack:
    def __init__(self):
        self.data = []

    def push(self, item):
        self.data.append(item)

    def pop(self):
        return self.data.pop() if self.data else None

    def peek(self):
        return self.data[-1] if self.data else None

    def is_empty(self):
        return len(self.data) == 0

    def size(self):
        return len(self.data)

# 사용 예시
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)
print(stack.pop())      # 3 (후입선출)
print(stack.peek())     # 2
print(stack.is_empty()) # False
print(stack.size())     # 2

📍 큐(Queue)

class Queue:
    def __init__(self):
        self.data = []

    def enqueue(self, item):
        self.data.append(item)

    def dequeue(self):
        return self.data.pop(0) if self.data else None

    def front(self):
        return self.data[0] if self.data else None

    def is_empty(self):
        return len(self.data) == 0

    def size(self):
        return len(self.data)

# 사용 예시
queue = Queue()
queue.enqueue(1)
queue.enqueue(2)
queue.enqueue(3)
print(queue.dequeue())    # 1 (선입선출)
print(queue.front())     # 2
print(queue.is_empty())  # False
print(queue.size())      # 2

📍 연결 리스트(Linked List)

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedList:
    def __init__(self):
        self.head = None

    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
            return
        last = self.head
        while last.next:
            last = last.next
        last.next = new_node

    def prepend(self, data):
        new_node = Node(data)
        new_node.next = self.head
        self.head = new_node

    def delete_with_value(self, data):
        if not self.head:
            return
        if self.head.data == data:
            self.head = self.head.next
            return
        current = self.head
        while current.next and current.next.data != data:
            current = current.next
        if current.next:
            current.next = current.next.next

    def find(self, data):
        current = self.head
        while current and current.data != data:
            current = current.next
        return current

    def display(self):
        current = self.head
        while current:
            print(current.data, end=' -> ')
            current = current.next
        print('None')

# 사용 예시
ll = LinkedList()
ll.append(1)
ll.append(2)
ll.append(3)
ll.display()            # 1 -> 2 -> 3 -> None
ll.prepend(0)
ll.display()            # 0 -> 1 -> 2 -> 3 -> None
ll.delete_with_value(2)
ll.display()            # 0 -> 1 -> 3 -> None
print(ll.find(3).data)  # 3

📍 트리(Tree) – 이진 탐색 트리(Binary Search Tree)

class TreeNode:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

class BinarySearchTree:
    def __init__(self):
        self.root = None

    def insert(self, data):
        if not self.root:
            self.root = TreeNode(data)
            return
        self._insert(self.root, data)

    def _insert(self, node, data):
        if data < node.data:
            if node.left:
                self._insert(node.left, data)
            else:
                node.left = TreeNode(data)
        else:
            if node.right:
                self._insert(node.right, data)
            else:
                node.right = TreeNode(data)

    def search(self, data):
        return self._search(self.root, data)

    def _search(self, node, data):
        if not node or node.data == data:
            return node
        if data < node.data:
            return self._search(node.left, data)
        return self._search(node.right, data)

    def inorder_traversal(self):
        return self._inorder_traversal(self.root, [])

    def _inorder_traversal(self, node, result):
        if node:
            self._inorder_traversal(node.left, result)
            result.append(node.data)
            self._inorder_traversal(node.right, result)
        return result

# 사용 예시
bst = BinarySearchTree()
bst.insert(10)
bst.insert(5)
bst.insert(15)
bst.insert(3)
bst.insert(7)
bst.insert(12)
bst.insert(18)
print(bst.inorder_traversal())  # [3, 5, 7, 10, 12, 15, 18]
print(bst.search(7).data)       # 7
print(bst.search(20))           # None

직접 구현의 장점

• 이해도 향상: 자료구조의 내부 동작 방식을 이해할 수 있습니다.
• 문제 해결 능력: 복잡한 문제를 해결할 때 적절한 자료구조를 선택하고 활용할 수 있습니다.
• 최적화 가능: 특정 상황에 맞춰 자료구조를 최적화할 수 있습니다.
• 코딩 면접 준비: 많은 코딩 면접에서 직접 자료구조를 구현하는 문제가 출제됩니다.

---

📚 3. 다양한 자료구조의 심화 이해

🔍 해시 테이블(Hash Table)

설명: 키-값 쌍으로 데이터를 저장하는 자료구조로, 해시 함수를 사용해 데이터를 빠르게 검색할 수 있습니다.

특징:

• 평균적으로 O(1)의 시간 복잡도로 검색, 삽입, 삭제가 가능.
• 충돌(Collision) 처리 방법 필요 (체이닝, 오픈 어드레싱 등).
• 순서를 유지하지 않음.

사용 예시:

• 딕셔너리: 파이썬의 dict는 해시 테이블을 기반으로 합니다.
• 캐시: 데이터 캐싱 시스템에서 빠른 데이터 접근을 위해 사용.

코드 예시:

class HashTable:
    def __init__(self, size=100):
        self.size = size
        self.table = [[] for _ in range(size)]

    def _hash(self, key):
        return hash(key) % self.size

    def set(self, key, value):
        index = self._hash(key)
        for pair in self.table[index]:
            if pair[0] == key:
                pair[1] = value
                return
        self.table[index].append([key, value])

    def get(self, key):
        index = self._hash(key)
        for pair in self.table[index]:
            if pair[0] == key:
                return pair[1]
        return None

    def delete(self, key):
        index = self._hash(key)
        for i, pair in enumerate(self.table[index]):
            if pair[0] == key:
                del self.table[index][i]
                return

# 사용 예시
ht = HashTable()
ht.set("apple", 1)
ht.set("banana", 2)
print(ht.get("apple"))   # 1
ht.set("apple", 3)
print(ht.get("apple"))   # 3
ht.delete("banana")
print(ht.get("banana"))  # None

🌾 힙(Heap)

설명: 완전 이진 트리의 일종으로, 부모 노드가 자식 노드보다 크거나 작은 성질을 유지하는 자료구조입니다. 주로 우선순위 큐 구현에 사용됩니다.

특징:

• 최대 힙(Max Heap): 부모 노드가 자식 노드보다 큼.
• 최소 힙(Min Heap): 부모 노드가 자식 노드보다 작음.
• 삽입과 삭제 연산이 O(log n) 시간 복잡도를 가짐.

사용 예시:

• 우선순위 큐: 작업 스케줄링, 다익스트라 알고리즘 등에서 사용.
• 힙 정렬: 효율적인 정렬 알고리즘 중 하나.

코드 예시:

import heapq

# 최소 힙
min_heap = []
heapq.heappush(min_heap, 3)
heapq.heappush(min_heap, 1)
heapq.heappush(min_heap, 2)
print(heapq.heappop(min_heap))  # 1
print(heapq.heappop(min_heap))  # 2
print(heapq.heappop(min_heap))  # 3

# 최대 힙 (힙에 음수를 넣어 최대 힙처럼 사용)
max_heap = []
heapq.heappush(max_heap, -3)
heapq.heappush(max_heap, -1)
heapq.heappush(max_heap, -2)
print(-heapq.heappop(max_heap))  # 3
print(-heapq.heappop(max_heap))  # 2
print(-heapq.heappop(max_heap))  # 1

🧩 트라이(Trie)

설명: 문자열을 효율적으로 저장하고 검색할 수 있는 트리의 일종으로, 각 노드가 하나의 문자를 저장합니다.

특징:

• 검색, 삽입, 삭제가 O(m) 시간 복잡도 (m은 문자열의 길이).
• 공간 효율성이 낮을 수 있지만, 문자열 검색에 최적화됨.

사용 예시:

• 자동 완성: 검색 엔진에서 단어 추천.
• 사전: 단어의 존재 여부를 빠르게 확인.

코드 예시:

class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_end_of_word = False

class Trie:
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word):
        current = self.root
        for char in word:
            if char not in current.children:
                current.children[char] = TrieNode()
            current = current.children[char]
        current.is_end_of_word = True

    def search(self, word):
        current = self.root
        for char in word:
            if char not in current.children:
                return False
            current = current.children[char]
        return current.is_end_of_word

    def starts_with(self, prefix):
        current = self.root
        for char in prefix:
            if char not in current.children:
                return False
            current = current.children[char]
        return True

# 사용 예시
trie = Trie()
trie.insert("apple")
trie.insert("app")
print(trie.search("app"))     # True
print(trie.search("appl"))    # False
print(trie.starts_with("appl")) # True

🌐 그래프(Graph)의 다양한 표현 방법

그래프는 노드와 간선으로 구성되며, 다양한 방식으로 표현할 수 있습니다.

인접 행렬(Adjacency Matrix)

• 설명: 노드 간의 연결을 2차원 배열로 표현.
• 장점: 간선의 존재 여부를 O(1) 시간에 확인 가능.
• 단점: 공간 복잡도가 O(V²)로, 희소 그래프에는 비효율적.

인접 리스트(Adjacency List)

• 설명: 각 노드에 연결된 노드들의 리스트를 저장.
• 장점: 공간 효율성이 높음, 특히 희소 그래프에 유리.
• 단점: 특정 간선의 존재 여부를 확인하는 데 시간이 걸릴 수 있음.

코드 예시 (인접 리스트):

class Graph:
    def __init__(self):
        self.adj_list = {}

    def add_vertex(self, vertex):
        if vertex not in self.adj_list:
            self.adj_list[vertex] = []

    def add_edge(self, vertex1, vertex2):
        self.add_vertex(vertex1)
        self.add_vertex(vertex2)
        self.adj_list[vertex1].append(vertex2)
        self.adj_list[vertex2].append(vertex1)  # 무방향 그래프인 경우

    def display(self):
        for vertex in self.adj_list:
            print(f"{vertex}: {self.adj_list[vertex]}")

# 사용 예시
g = Graph()
g.add_edge("A", "B")
g.add_edge("A", "C")
g.add_edge("B", "D")
g.add_edge("C", "D")
g.display()
# 출력:
# A: ['B', 'C']
# B: ['A', 'D']
# C: ['A', 'D']
# D: ['B', 'C']

📈 균형 잡힌 트리(Balanced Tree)

설명: 트리의 높이를 최소화하여 연산의 시간 복잡도를 최적화한 트리 구조.

종류:

• AVL 트리: 모든 노드에서 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 최대 1.
• 레드-블랙 트리(Red-Black Tree): 균형을 유지하면서 삽입과 삭제 시 색상 규칙을 통해 트리를 재조정.

특징:

• 삽입, 삭제, 검색 연산이 O(log n) 시간 복잡도를 가짐.
• 균형을 유지하여 최악의 경우에도 성능 저하를 방지.

코드 예시 (AVL 트리 간단 구현):

class AVLNode:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.height = 1

class AVLTree:
    def insert(self, root, key):
        if not root:
            return AVLNode(key)
        elif key < root.key:
            root.left = self.insert(root.left, key)
        else:
            root.right = self.insert(root.right, key)

        root.height = 1 + max(self.get_height(root.left), self.get_height(root.right))

        balance = self.get_balance(root)

        # LL Case
        if balance > 1 and key < root.left.key:
            return self.right_rotate(root)

        # RR Case
        if balance < -1 and key > root.right.key:
            return self.left_rotate(root)

        # LR Case
        if balance > 1 and key > root.left.key:
            root.left = self.left_rotate(root.left)
            return self.right_rotate(root)

        # RL Case
        if balance < -1 and key < root.right.key:
            root.right = self.right_rotate(root.right)
            return self.left_rotate(root)

        return root

    def left_rotate(self, z):
        y = z.right
        T2 = y.left

        y.left = z
        z.right = T2

        z.height = 1 + max(self.get_height(z.left), self.get_height(z.right))
        y.height = 1 + max(self.get_height(y.left), self.get_height(y.right))

        return y

    def right_rotate(self, z):
        y = z.left
        T3 = y.right

        y.right = z
        z.left = T3

        z.height = 1 + max(self.get_height(z.left), self.get_height(z.right))
        y.height = 1 + max(self.get_height(y.left), self.get_height(y.right))

        return y

    def get_height(self, node):
        if not node:
            return 0
        return node.height

    def get_balance(self, node):
        if not node:
            return 0
        return self.get_height(node.left) - self.get_height(node.right)

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.key)
            res = res + self.inorder_traversal(root.right)
        return res

# 사용 예시
avl = AVLTree()
root = None
keys = [10, 20, 30, 40, 50, 25]
for key in keys:
    root = avl.insert(root, key)
print(avl.inorder_traversal(root))  # [10, 20, 25, 30, 40, 50]

직접 구현해보면, 왜 배열 접근이 O(1)인지, 연결 리스트 검색이 왜 O(n)인지 등을 훨씬 직관적으로 알 수 있게 됩니다.

---

🎯 4. 실생활에서 자료구조가 얼마나 중요할까?

✅ (1) 검색 속도를 높이는 자료구조

구글 검색:
구글에서 검색할 때 0.1초 만에 결과가 나오는 이유는 트라이(Trie), 해시 테이블(Hash Table) 같은 고급 자료구조 덕분입니다. 트라이는 단어의 공통 접두사를 공유하여 검색 효율을 높이고, 해시 테이블은 빠른 키-값 검색을 가능하게 합니다.

예시:

• 자동 완성: 사용자가 입력하는 단어의 접두사를 기반으로 가능한 완성 단어를 빠르게 추천.
• 검색 엔진 인덱스: 웹 페이지의 내용을 빠르게 검색할 수 있도록 인덱싱.

✅ (2) SNS에서 친구 추천하는 그래프

페이스북의 "이 사람을 아시나요?":
페이스북이 "이 사람을 아시나요?"라고 추천할 때, 그래프(Graph)를 이용해 친구 관계를 분석합니다. 친구 관계는 그래프의 노드와 간선으로 표현되며, 연결된 친구의 친구를 추천하는 방식으로 구현됩니다.

예시:

• 친구 추천 알고리즘: 공통 친구 수, 상호작용 빈도 등을 분석하여 친구를 추천.
• 커뮤니티 탐지: 서로 밀접하게 연결된 사용자 그룹을 찾아내어 타겟 마케팅에 활용.

✅ (3) 게임에서 최적의 경로 찾기

게임에서 적을 피해 빠르게 도망가야 할 때:
게임에서 캐릭터가 적을 피하거나 목표 지점으로 이동할 때, 그래프 탐색 알고리즘(BFS, DFS, A*)이 최단 경로를 찾는 데 쓰여요. 이러한 알고리즘은 게임의 실시간 성능에 큰 영향을 미칩니다.

예시:

• 길찾기: 게임 내 맵에서 최단 경로를 찾아 이동.
• AI 동작: 적 캐릭터의 이동 경로 결정.

✅ (4) 데이터베이스 인덱싱

데이터베이스:
대규모 데이터베이스에서 데이터를 빠르게 검색하고 관리하기 위해 다양한 자료구조가 사용됩니다. B-트리(B-Tree), 비트맵 인덱스(Bitmap Index) 등이 대표적입니다.

예시:

• 인덱스: 테이블의 특정 컬럼에 인덱스를 생성하여 검색 속도를 향상.
• 트랜잭션 관리: 데이터 무결성을 유지하기 위해 트리 기반 자료구조 사용.

✅ (5) 네트워크 라우팅

네트워크:
인터넷과 같은 대규모 네트워크에서는 데이터 패킷을 최적의 경로로 전달하기 위해 그래프 기반 알고리즘이 사용됩니다.

예시:

• 라우팅 프로토콜: OSPF(Open Shortest Path First), BGP(Border Gateway Protocol) 등은 그래프 알고리즘을 기반으로 최적 경로를 계산.
• 네트워크 토폴로지 관리: 효율적인 데이터 전송과 네트워크 안정성을 위해 자료구조 활용.

✅ (6) 머신러닝과 인공지능

머신러닝:
머신러닝 알고리즘은 대규모 데이터를 처리하고 분석하기 위해 다양한 자료구조를 사용합니다. 행렬(Matrix), 텐서(Tensor), 그래프 등이 대표적입니다.

예시:

• 신경망: 데이터를 계층적으로 처리하기 위해 트리나 그래프 구조 사용.
• 데이터 전처리: 효율적인 데이터 저장과 접근을 위해 해시 테이블, 배열 사용.

✅ (7) 운영 체제와 파일 시스템

운영 체제:
운영 체제는 프로세스 관리, 메모리 관리, 파일 시스템 관리 등에서 다양한 자료구조를 사용합니다.

예시:

• 프로세스 스케줄링: 큐(Queue)를 사용하여 실행할 프로세스를 관리.
• 메모리 관리: 해시 테이블과 트리를 사용하여 메모리 할당과 해제를 효율적으로 처리.
• 파일 시스템: B-트리와 같은 자료구조를 사용하여 파일과 디렉토리를 관리.

---

🏆 5. 자료구조를 공부하면 뭐가 좋을까?

✅ 코딩 면접 합격률 UP

많은 기업의 코딩 면접에서는 자료구조와 알고리즘 문제가 출제됩니다. 자료구조를 잘 이해하고 직접 구현할 줄 알면, 문제 해결 능력을 효과적으로 어필할 수 있어 면접 합격률이 높아집니다.

예시:

• LeetCode, HackerRank 같은 플랫폼에서 자주 출제되는 문제들.
• 자료구조 기반 문제 해결: 링크드 리스트를 역순으로 뒤집기, 트리를 이용한 탐색 등.

✅ 더 빠르고 효율적인 코드 작성

적절한 자료구조를 선택하면 코드의 성능이 크게 향상됩니다. 예를 들어, 데이터 검색이 빈번한 경우 해시 테이블을 사용하면 검색 속도를 대폭 향상시킬 수 있습니다.

예시:

• 검색 최적화: 데이터베이스 쿼리 시 인덱스를 활용하여 검색 속도 향상.
• 메모리 관리: 연결 리스트를 사용하여 동적 데이터 관리.

✅ 실제 개발에서 최적의 해결책을 찾는 능력

복잡한 문제를 해결할 때, 자료구조를 통해 최적의 해결책을 설계할 수 있습니다. 예를 들어, 대규모 데이터 처리 시 적절한 자료구조를 사용하면 시스템의 확장성과 안정성을 높일 수 있습니다.

예시:

• 대규모 데이터 처리: 빅데이터 분석에서 효율적인 자료구조 활용.
• 실시간 시스템: 게임, 금융 시스템 등에서 실시간 데이터 처리를 위한 최적화.

✅ 문제 해결 능력 향상

자료구조를 학습하면서 다양한 문제를 해결해보면 논리적 사고와 문제 해결 능력이 향상됩니다. 이는 개발자로서의 역량을 크게 높여줍니다.

예시:

• 알고리즘 문제 해결: 다양한 자료구조를 활용한 문제 해결 경험.
• 프로젝트 개발: 실무 프로젝트에서 최적의 자료구조 선택과 구현.

✅ 소프트웨어 최적화와 유지보수 용이

잘 설계된 자료구조는 소프트웨어의 성능을 최적화하고, 유지보수를 용이하게 만듭니다. 코드의 가독성이 높아지고, 새로운 기능을 추가하기도 쉬워집니다.

예시:

• 모듈화된 코드: 자료구조를 모듈화하여 코드의 재사용성과 유지보수성을 높임.
• 성능 모니터링: 자료구조의 효율성을 분석하고 최적화하여 시스템 성능을 향상.

---

🛠️ 6. 자료구조를 효과적으로 학습하는 방법

✅ 체계적인 학습 계획 세우기

자료구조는 방대한 주제이므로 체계적인 학습 계획이 필요합니다. 기본 자료구조부터 시작해 점차 복잡한 자료구조로 나아가는 것이 좋습니다.

학습 단계:

1. 기초 자료구조: 배열, 스택, 큐, 링크드 리스트.
2. 트리와 그래프: 이진 트리, 이진 탐색 트리, 힙, 그래프.
3. 고급 자료구조: 해시 테이블, 트라이, 균형 잡힌 트리.
4. 응용 자료구조: 세그먼트 트리, 펜윅 트리 등.

✅ 이론과 실습 병행하기

자료구조를 학습할 때는 이론적인 개념을 이해하는 것뿐만 아니라, 실제로 구현해보는 것이 중요합니다. 이를 통해 자료구조의 동작 원리를 깊이 있게 이해할 수 있습니다.

방법:

• 코드 구현: 각 자료구조를 직접 구현해보고, 다양한 연산을 수행해보세요.
• 문제 풀이: 알고리즘 문제를 풀면서 자료구조를 적용해보세요.
• 프로젝트 적용: 간단한 프로젝트를 통해 자료구조를 실제로 사용해보세요.

✅ 시각화 도구 활용하기

자료구조는 시각적으로 이해하면 더 쉽게 학습할 수 있습니다. 다양한 시각화 도구를 활용하여 자료구조의 동작을 시각적으로 확인해보세요.

추천 도구:

• Visualgo: 다양한 자료구조와 알고리즘을 시각화해주는 웹사이트.
• Draw.io: 직접 자료구조를 그려보며 이해를 돕는 도구.

✅ 참고서와 온라인 강의 활용하기

좋은 참고서와 온라인 강의를 통해 체계적으로 자료구조를 학습할 수 있습니다. 유명한 자료구조 교재나 온라인 강의를 참고해보세요.

추천 자료:

• 책:
  • "Introduction to Algorithms" by Cormen, Leiserson, Rivest, and Stein
  • "Data Structures and Algorithms in Python" by Michael T. Goodrich
• 온라인 강의:
  • Coursera의 "Data Structures and Algorithms" 강좌
  • edX의 "Algorithm Design and Analysis" 강좌
  • YouTube의 다양한 자료구조 강의

✅ 꾸준한 연습과 복습

자료구조는 한 번에 완전히 이해하기 어렵습니다. 꾸준히 연습하고, 주기적으로 복습하여 지식을 확고히 다지세요.

방법:

• 일일 문제 풀이: 매일 하나씩 자료구조 관련 문제를 풀어보세요.
• 스터디 그룹 참여: 다른 사람들과 함께 공부하며 이해도를 높이세요.
• 노트 정리: 학습한 내용을 정리하고, 중요한 개념을 노트에 기록하세요.

---

📢 결론: 자료구조 마스터에 도전해보세요! 💪🔥

자료구조는 단순히 이론적인 지식이 아니라, 실무에서의 문제 해결과 성능 최적화에 필수적인 도구입니다. 라이브러리를 잘 활용하는 것도 중요하지만, 직접 구현해 보는 경험이 문제 해결 능력을 크게 향상시킵니다.

자료구조를 학습하면 얻을 수 있는 주요 혜택

• 코딩 면접 합격률 UP: 면접에서 자주 출제되는 자료구조 문제를 해결할 수 있습니다.
• 더 빠르고 효율적인 코드 작성: 적절한 자료구조 선택으로 코드 성능을 최적화할 수 있습니다.
• 실제 개발에서 최적의 해결책을 찾는 능력: 복잡한 문제를 효율적으로 해결할 수 있는 능력을 갖추게 됩니다.
• 문제 해결 능력 향상: 논리적 사고와 창의적 문제 해결 능력이 강화됩니다.
• 소프트웨어 최적화와 유지보수 용이: 코드의 가독성과 유지보수성이 향상됩니다.

마지막으로, 자료구조를 마스터하기 위한 팁

1. 기초부터 탄탄히: 기본 자료구조를 확실히 이해하고 넘어가세요.
2. 다양한 문제 풀기: 다양한 알고리즘 문제를 풀며 실력을 키우세요.
3. 실제 구현 경험: 직접 자료구조를 구현해보며 이해도를 높이세요.
4. 지속적인 학습: 새로운 자료구조와 알고리즘을 꾸준히 학습하세요.
5. 커뮤니티 참여: 스터디 그룹이나 온라인 커뮤니티에 참여해 다른 사람들과 지식을 공유하세요.

📢 자료구조 마스터에 도전해보세요! 💪🔥 여러분의 프로그래밍 실력을 한층 더 높여줄 자료구조의 세계에 뛰어들어 보세요. 꾸준한 노력과 학습을 통해 자료구조의 전문가가 되어, 더 나은 코드와 효율적인 문제 해결 능력을 갖추시길 바랍니다!