자바스크립트에서 0.1+0.2를 하게되면 0.3이 나올 것 같지만, 결과는 다르다.
> 0.1 + 0.2
< 0.30000000000000004 왜 이런 결과가 나오게 되는 것일까?
부동소수점(Floating Point)
모든 컴퓨터들은 자료를 비트와 바이트 (bit & byte)로 저장한다. 비트는 컴퓨터에서 사용하는 가장 작은 데이터 단위이고, 하나의 비트는 2진수로 표현 1 혹은 0으로만 표현되어 데이터를 처리하고, 데이터를 처리, 저장, 전송할 때 사용하게 된다.
하나의 바이트는 8개의 비트로 구성되어 있다. 흔히 말하는 8비트, 16비트 등의 표현은 1바이트, 2바이트와 동일하다.
컴퓨터 프로그램에 인간이 사용하는 숫자 체계인 10진수를 입력하더라도, 컴퓨터 메모리에 저장될 때에는 64비트의 부동소수점(floating point) 체계로 저장된다.
- 정수 (0, 1, -1, 2, -2 등의 자연수)
- 정수가 아닌 유리수 (유한 소수, 순환되지 않는 무한 소수)
- 순환하는 무한 소수
- n진수 (8진수, 16진수 등)
등 어떠한 숫자를 입력하게 되어도, 모든 숫자, 모든 자료형은 64비트짜리 컴퓨터 메모리에 2진수로 저장된다는 것이다.
NaN과 같은 표현 불가능한 결과는 제외한다.
0.1 + 0.2 === 0.30000000000000004
그래서 왜 이런 결과가 나오는지 구체적으로 살펴보자면,
10진수에서 2진수로 연산된 수를 Binary Floating Point 라고 한다.
가령 23, 24 등의 10진수 정수는 1의 자리(10의 0제곱)와 10의 자리(10의 1제곱)이 합산된 값이나, 컴퓨터는 이러한 단위가 10의 제곱이 아닌 2의 제곱으로 받아들이고 해석한다. 이러한 연산 방법을 사용할 때 정수를 계산하는 것은 큰 문제가 되지 않지만, 소수점은 정확히 떨어지지 않는 문제가 발생한다.
예를 들어 정수 10을 2진수로 표현하자면 1010 이지만, 10.2를 2진수로 표현하려고 하면 어떻게 될까?
10.2 는 10과 0.2 (2/10)을 합한 값이기 때문에 이 0.2를 2진수로 표현해야 한다. 2진법에서 소숫점을 연산하는 방법도 정수를 연산하는 방법과 크게 다르지 않다. 2에 음의 지수를 사용하여 지수가 1씩 줄어든 제곱값을 합산한다.
2진법에서의 소숫점의 연산은 2의 제곱값을 분모로 사용한 1/2, 1/4, 1/8 ... 단위로 수행된다. 따라서, 10진수 0.5를 2진수로 표현하면 0.1이 되는 것이고, 10진수 0.75는 0.5 + 0.25 인 0.11 이 된다.
그렇다면 0.1과 같은 값은 어떻게 연산하는 것일까?
0.1은 2진수 단위의 제곱값들의 조합을 통해 연산을 수행해도 정확히 떨어지는 값을 내기 어렵다. 이런 경우 계속해서 2진수의 소숫점을 따라 내려가 연산을 하다가, 무한 연산의 굴레에 빠지게 되는 것이다.
10진수 0.1의 2진수 표현값은 0.000111111... 으로 시작하는 무한 소수가 되겠지만, 컴퓨터의 비트 수에는 제한이 있다는 것이 중요하다.
비트 하나당 이진수 하나를 표현하기 때문에, 64비트 컴퓨터를 사용한다면 모든 비트를 소숫점 표현에 할애한다고 해도 무한 소수를 다 담을 수 없다.
따라서 0.1과 0.2의 연산 결과는 10진수로는 0.3이지만, 2진수로 표현하면 비트의 한계 때문에 근사값 0.30000000000000004 이 표시되게 되는 것이다.
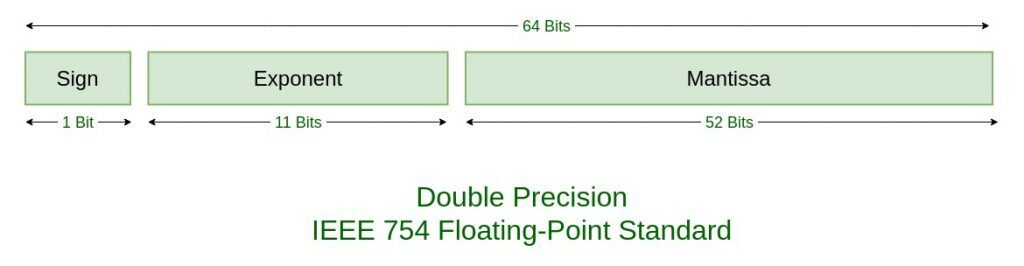
- 비트부호(Sign Bit) : 해당 숫자가 음수인지 양수인지 표현하는 자리, 0이면 양(+) 1이면 음(-), 1 Bit의 공간을 차지
- 지수부(Exponent) : 지수를 나타낸다(정수 처리), 11 Bit의 공간을 차지
- 가수부(Mantissa) : 가수 또는 유효숫자를 나타낸다(소수 처리), 52 Bit의 공간을 차지
