풀이

1. 스티커를 붙이는 방법에 대해서 생각해보자. 일단 모눈종이 안에 스티커를 집어 넣어야한다. 문제에 두 스티커가 겹치면 안된다는 매우 중요한 조건이 있다. 그리고 스티커를 90도 회전하는 것도 가능하다. 당연히 모눈종이에서 스티커가 벗어나는 것도 안된다.

2. 스티커는 주어진 여러개의 스티커중에 딱 2개만 골라서 모눈종이 위에 붙이는 것이다.
   
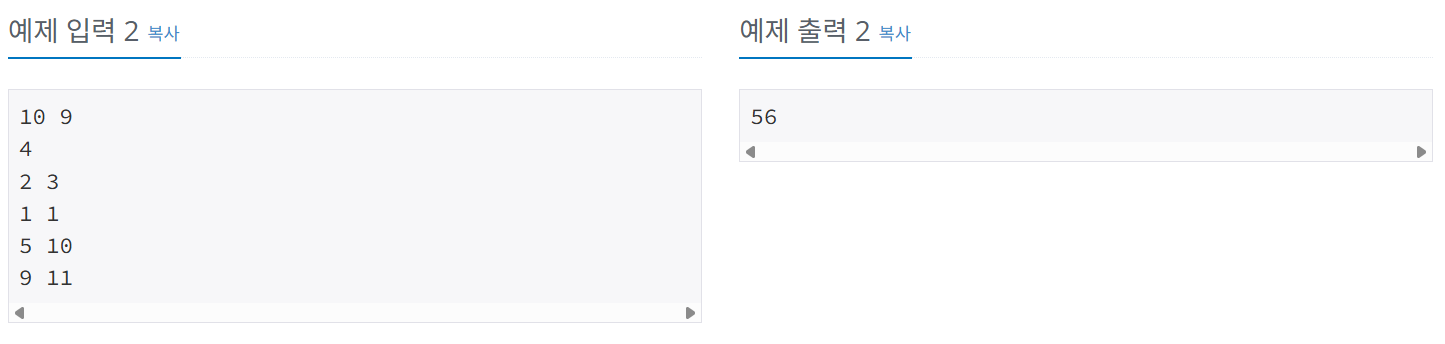
   위의 예시의 경우 $_4C_2$가 된다. 당연히 순서 상관없이 2개를 선택하면 되기 때문이다. 그리고 각 스티커의 높이와 너비가 주어졌다.

3. 스티커는 아래로 붙이거나 옆에 붙이는 것 밖에 방법이 없다.

   
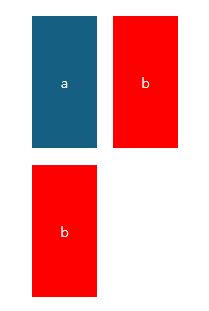
   위의 사진과 같이, 어차피 90도까지 밖에 회전이 안되기 때문에 a의 좌측 상단을 0,0에 고정한 다음, 오른쪽에 붙이거나 아래 붙이는 방법 뿐이다.

4. 이제 스티커를 붙이는 방법에 대해서 생각해냈으니, 실제 붙일 수 있는지 없는지 조건식만 수립하면, 전체 경우 $_nC_2$에서 가능한 경우들을 뽑아낼 수 있다.

5. 이해를 하기 편하게 a도형의 높이와 너비는 r1,c1 그리고 b도형의 높이와 너비는 r2,c2로 설정하고 서로 다른 값이라고 해보자.
   

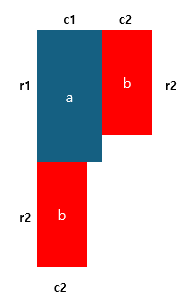
위의 그림을 잘 살펴보면, a 옆에 b를 붙이는 경우와 a 아래에 b를 붙이는 경우 모눈종이에 들어가려면 어떻게 해야하는지 눈에 들어온다.

• 옆에 붙이는 경우
  두 너비를 더한 값은 $c1+c2 < W$ 두 높이 중 큰 값이 $max(r1,r2)<H$ 조건을 만족해야한다.
• 아래에 붙이는 경우
  두 너비중 큰 값이 $max(c1,c2)<W$ 그리고, 두 높이를 더한 값이 $r1+r2<H$ 조건을 만족해야한다.

6. a,b로 선택된 도형이 둘다 90도로 회전할 수 있기 때문에 이를 반영하면 총 8가지 경우의 수가 나온다. (a그대로 b그대로 부터 a회전 b회전까지)

7. 위의 내용을 코드로 옮겨보자

# 16937 두 스티커
from itertools import combinations
h,w=map(int,input().split())
s=int(input())
stickers=[list(map(int,input().split())) for _ in range(s)]
ans=[]
cases=list(combinations(range(s),2))

for case in cases:
    a,b=case
    r1,c1=stickers[a]
    r2,c2=stickers[b]
    # 옆으로 붙이는 경우
    if max(r1,r2)<=h and c1+c2<=w:
        ans.append(r1*c1+r2*c2)
        continue
    # 옆으로 붙이는 경우 A rotate
    if max(c1,r2)<=h and r1+c2<=w:
        ans.append(r1*c1+r2*c2)
        continue
    # 옆으로 붙이는 경우 B rotate
    if max(r1,c2)<=h and c1+r2<=w:
        ans.append(r1*c1+r2*c2)
        continue
    # 옆으로 붙이는 경우 A,B rotate
    if max(c1,c2)<=h and r1+r2<=w:
        ans.append(r1*c1+r2*c2)
        continue

    # 위아래로 붙이는 경우
    if r1+r2<=h and max(c1,c2)<=w:
        ans.append(r1*c1+r2*c2)
        continue
    # 위아래로 붙이는 경우 A rotate
    if c1+r2<=h and max(r1,c2)<=w:
        ans.append(r1*c1+r2*c2)
        continue
    # 위아래로 붙이는 경우 B rotate
    if r1+c2<=h and max(c1,r2)<=w:
        ans.append(r1*c1+r2*c2)
        continue
    # 위아래로 붙이는 경우 A,B rotate
    if c1+c2<=h and max(r1,r2)<=w:
        ans.append(r1*c1+r2*c2)
        continue


if len(ans)==0:
    print(0)
    exit()
print(max(ans))

python을 잘하는 편은 아니라 무식하게 짰다. 만약에 모눈종이에 들어갈 수 있다면, 어차피 겹칠일이 없기 때문에, r1*c1+r2*c2로 각 스티커의 넓이를 더해서 정답 후보군에 추가해주면 된다.

정답 후보가 하나도 없다면 당연히 0을 출력하고 후보들이 있다면 그중에서 가장 큰값으로 제출하자!

여기서, 시간 복잡도는 $_NC_2$ 에서 대충 $N^2$ 잡아주고, 뒤에 각 경우마다 8가지라고 해도 O($N^2$)이기에 시간 초과될 일은 없을 것 같다.