다익스트라 알고리즘이 음수 가중치가 불가능한 이유
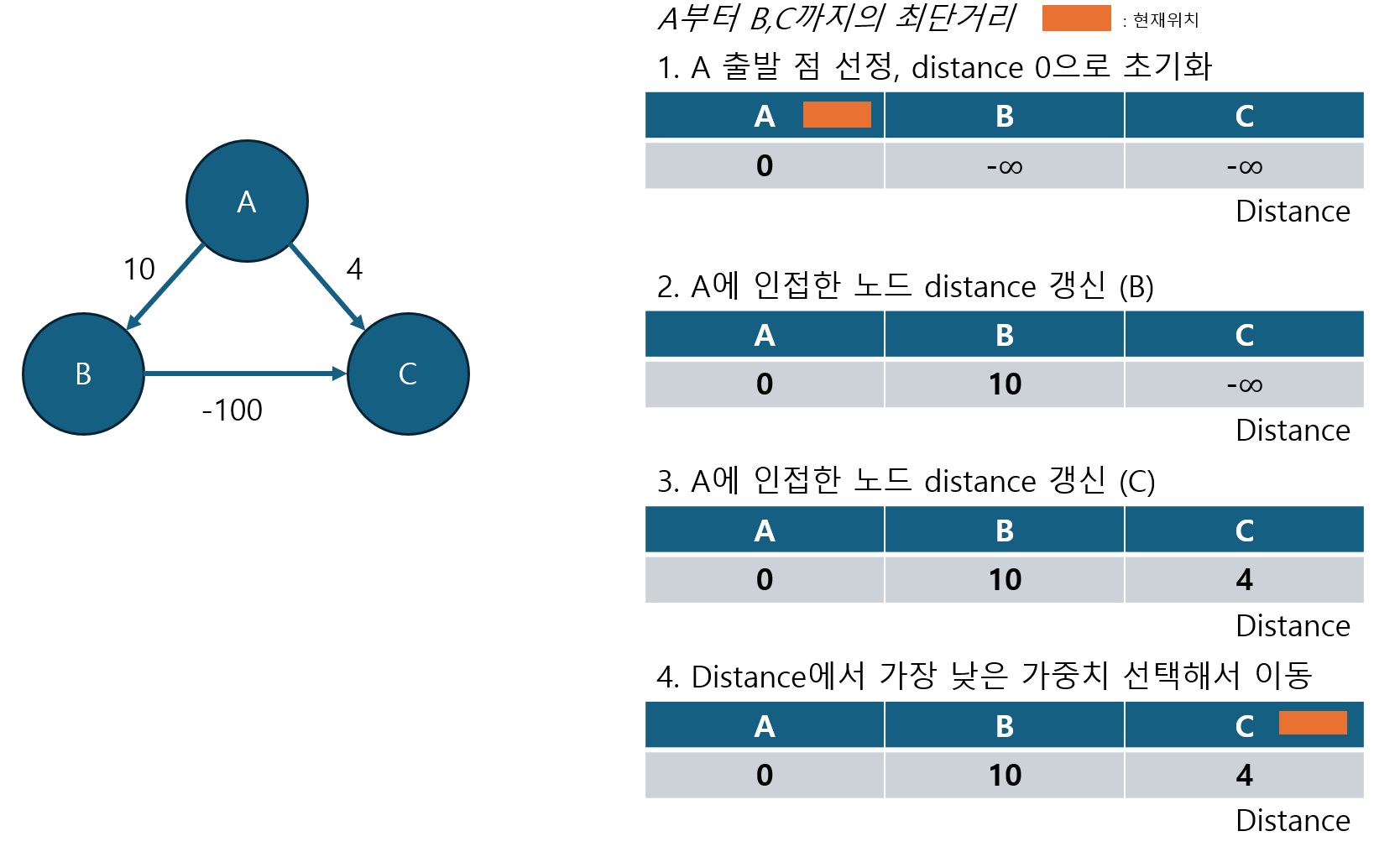
위의 사진은 다익스트라 알고리즘의 과정을 의미한다. 최종적으로 우리가 구하고 싶은 것은, 시작노드에서 다른 노드까지의 최단거리이다. 하지만, 위의 경우, 그리디 알고리즘 기반으로 하는 다익스트라 알고리즘은 4 가중치인 노드를 먼저 방문하기 때문에, -90의 결과를 얻을 수 없다.
벨만 포드 알고리즘
다익스트라 알고리즘과 동일하게, 한 노드에서 다른 모드 노드까지의 최단 경로를 구하는 알고리즘이다. 다익스트라와의 차이점은 음의 가중치가 존재하는 그래프에도 사용할 수 있다는 것이다. 하지만, 매 단계마다 모든 간선을 전부 확인해서 노드 간 최단 거리를 구해가기 때문에, 더 오래 걸린다.
연산과정
- 시작점을 초기화한다.
다익스트라 알고리즘과 동일하게 최초의 시작 노드를 초기화한다. distance 배열을 따로 생성하여, 각 노드 별로 최소 가중치를 갱신하자.
distance=[INF]*n
distance[start]=0
- 시작점에서 다른 노드에 방문하는 과정에서, 각 노드에 방문할때마다, 모든 가중치를 update한다.
벨만 포드 알고리즘의 특징은 이 부분에서 나타난다. 다익스트라 알고리즘은 인접한 노드에 대해서만 가중치를 비교하고, distance에서 최소 가중치를 고른다. 이와 다르게, 모든 노드에 방문할때마다, 지금 방문하지 않는 노드라고 해도, 간선의 가중치를 모두 계산해서, distance 배열을 update해준다.
for i in range(v) # 모든 노드에 방문할때마다
for j in range(e) # 모든 간선에 대해서 update를 진행한다.
- graph에 대한 이해
벨만 포드, 다익스트라 알고리즘 모두 그래프를 배열이나 딕셔너리로 표현할 줄 알아야한다. 사진의 graph 상황은 아래와 같이 표현 가능하다.
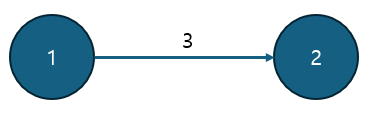
graph=[]
start,end,distance=map(int,input().split())
graph.append((start,end,distance)) # list로 표현하는 방법 (시작점,도착점,가중치)
>>[(1,2,3)]
---------
from collections import defaultdict
graph=defaultdict(list)
start,end,distance=map(int,input().split())
graph[start].appned((end,distance))
>>{1:(2,3)}
- cost 계산 후 update
for i in range(v) # 모든 노드에 방문할때마다
for j in range(e) # 모든 간선에 대해서 update를 진행한다.2번 의 반복문에 이어서, 가중치를 update해주는 알고리즘을 작성해준다. 최소 가중치를 계산하는 것이기 때문에, 현재 노드까지의 가중치+다음 노드로 이동하는 데에 드는 가중치 의 결과가 다음 노드에 저장된 가중치 보다 작으면 update하는 것이다. 각각은 아래와 같이 표현할 수 있다. (list graph 기준)
현재 노드까지의 가중치=graph[j][0]다음 노드로 이동하는 데에 드는 가중치=graph[j][2]다음 노드=graph[j][1]다음 노드에 저장된 가중치=distance[graph[j][1]]
이를 종합해 알고리즘을 구현하면 아래와 같이 설정할 수 있다.
for i in range(v) # 모든 노드에 방문할때마다
for j in range(e) # 모든 간선에 대해서 update를 진행한다.
cur_node=graph[j][0]
next_node=graph[j][1]
cost=graph[j][2]
if distance[next_node]>distance[cur_node]+cost: # 현재 위치 방문한 후 next_node 방문시 가중치가 더 작은 경우 update
distance[next_node]=distance[cur_node]+cost여기에서, 현재 node의 distance가 INF인 경우는 제외하자. 이는, 해당 노드까지 갈 수 있는 경로가 아직 등장하지 않았다는 뜻인데, 그런 노드에서 다음 노드를 이동해봤자 INF+1과 같은 계산이 되기 때문이다.
최종적으로 간선을 업데이트 하는 알고리즘은 아래와 같이 구현할 수 있다.
for i in range(v) # 모든 노드에 방문할때마다
for j in range(e) # 모든 간선에 대해서 update를 진행한다.
cur_node=graph[j][0]
next_node=graph[j][1]
cost=graph[j][2]
if distance[cur_node]!=INF and distance[next_node]>distance[cur_node]+cost:
# 현재 위치 방문한 후 next_node 방문시 가중치가 더 작은 경우 update
distance[next_node]=distance[cur_node]+cost하지만, 우리는 벨만 포드 알고리즘에서 가장 중요한 특징 하나를 아직 다루지 않았다 그것은 바로 음의 사이클 이다.
음의 사이클
말 그대로 사이클을 돌았을때 음의 값이 되는 경우를 의미한다. 아래의 그래프를 살펴보자.
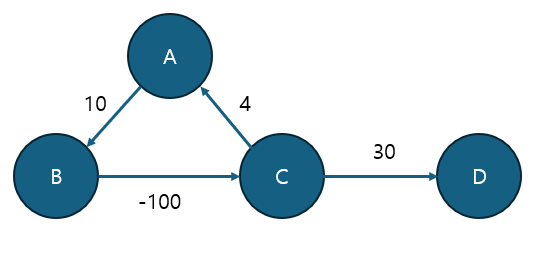
A에서 출발해 제자리로 돌아오면 음의 가중치가 되는 것을 알 수 있다. 이렇게 되면, 사실상 시작점 A를 제외한 모든 노드로의 최단거리는 음의 무한대가 된다. 한번의 cycle에서 -86이 되고, 한번 더 돌면, -172가 된다. 점점 음의 무한대에 가까워지게 가중치를 update할 수 있고, B,C,D까지 사실상 최단거리가 음의 무한대가 된다.
이를 코드 단위에서 확인하려면, 이전의 update 과정에서 조건문을 하나 더 추가해야한다.
for i in range(v) # 모든 노드에 방문할때마다
for j in range(e) # 모든 간선에 대해서 update를 진행한다.
cur_node=graph[j][0]
next_node=graph[j][1]
cost=graph[j][2]
if distance[cur_node]!=INF and distance[next_node]>distance[cur_node]+cost:
# 현재 위치 방문한 후 next_node 방문시 가중치가 더 작은 경우 update
distance[next_node]=distance[cur_node]+cost
if i==v-1:
print("MINUS CYCLE")update는 사실 node의 개수-1까지만 진행해도 된다. 왜냐면, 한 번 방문한 정점을 또 방문하면 사이클이 되기 때문이다. 우리는 중복되지 않는 최단 경로를 구하려는 거니까, 한 정점은 한 번만 거치게 되는 게 정상이다. 즉, 사이클이 없는 경로의 최대 길이 는 V-1개의 간선이라는 것이다.
따라서, if i==v-1 즉, v번쨰(0부터 loop가 시작되기 때문에 v-1)에도 update가 이뤄지면 음의 사이클이라는 것을 알 수 있다.
아래는 음의 사이크 성질을 이용해서 풀 수 있는 문제이다. 생각보다 쉬우니 풀어보기를! (사진을 누르면 문제로 이동할 수 있다.)
최종 코드
INF=1e9
v,e=map(int,input().split())
graph=[]
for _ in range(e):
start,end,cost=map(int,input().split())
graph.append((start,end,cost))
distance=[INF]*v
def Bellman_ford(start):
distance[start]=0
for i in range(v): # 모든 노드에 방문할때마다
for j in range(e): # 모든 간선에 대해서 update를 진행한다.
cur_node=graph[j][0]
next_node=graph[j][1]
cost=graph[j][2]
if distance[cur_node]!=INF and distance[next_node]>distance[cur_node]+cost:
# 현재 위치 방문한 후 next_node 방문시 가중치가 더 작은 경우 update
distance[next_node]=distance[cur_node]+cost
if i==v-1:
print("MINUS CYCLE")
Bellman_ford(1) # 1을 시작점으로 하는 벨만포드 알고리즘긴 글 읽어주셔서 감사합니다.