MST 알고리즘에는 크게 두 가지 알고리즘이 있다.
- Kruskal MST 알고리즘
- Prim MST 알고리즘
MST 알고리즘을 설명하기 이전에 기본 개념부터 설명한다.
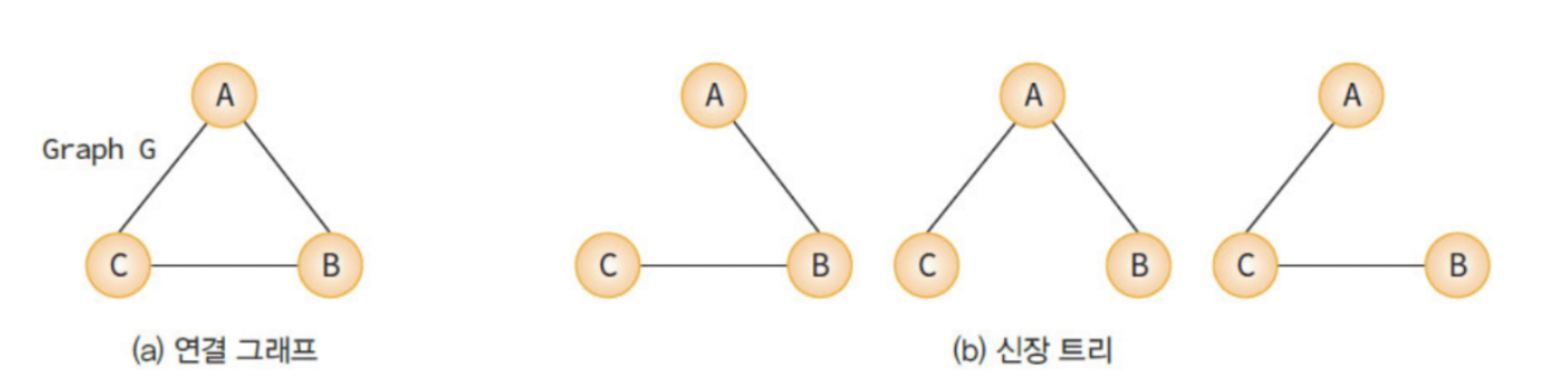
신장 트리(spanning tree)
- 그래프 내의 모든 정점을 포함하는 트리
- 모든 정점들이 연결되어 있어야 하고 사이클을 포함해서는 안된다.
- n개의 정점을 가지는 그래프의 신장 트리는 n-1개의 간선을 가진다.
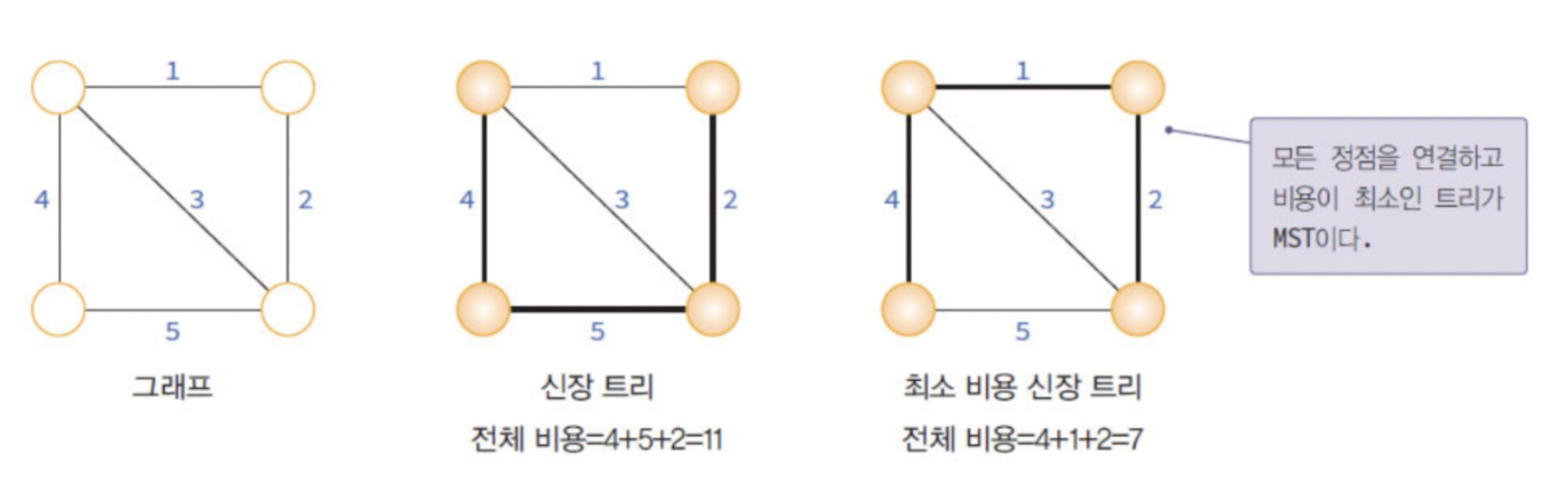
최소비용 신장 트리
- 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결된다.
- MST는 최소 비용의 간선으로 구성됨과 동시에 사이클을 포함하지 않아야 한다.
- MST의 응용
- 도로 건설, 전기 회로, 배관, 통신
Kruskal의 MST 알고리즘
- 탐욕적인 방법(greedy method)
- 주요 알고리즘 설계 기법
- 각 단계에서 최선의 답을 선택하는 과정을 반복함으로써 최종적인 해답에 도달한다.
- 탐욕적인 방법은 항상 최적의 해답을 주는지 검증이 필요하다.
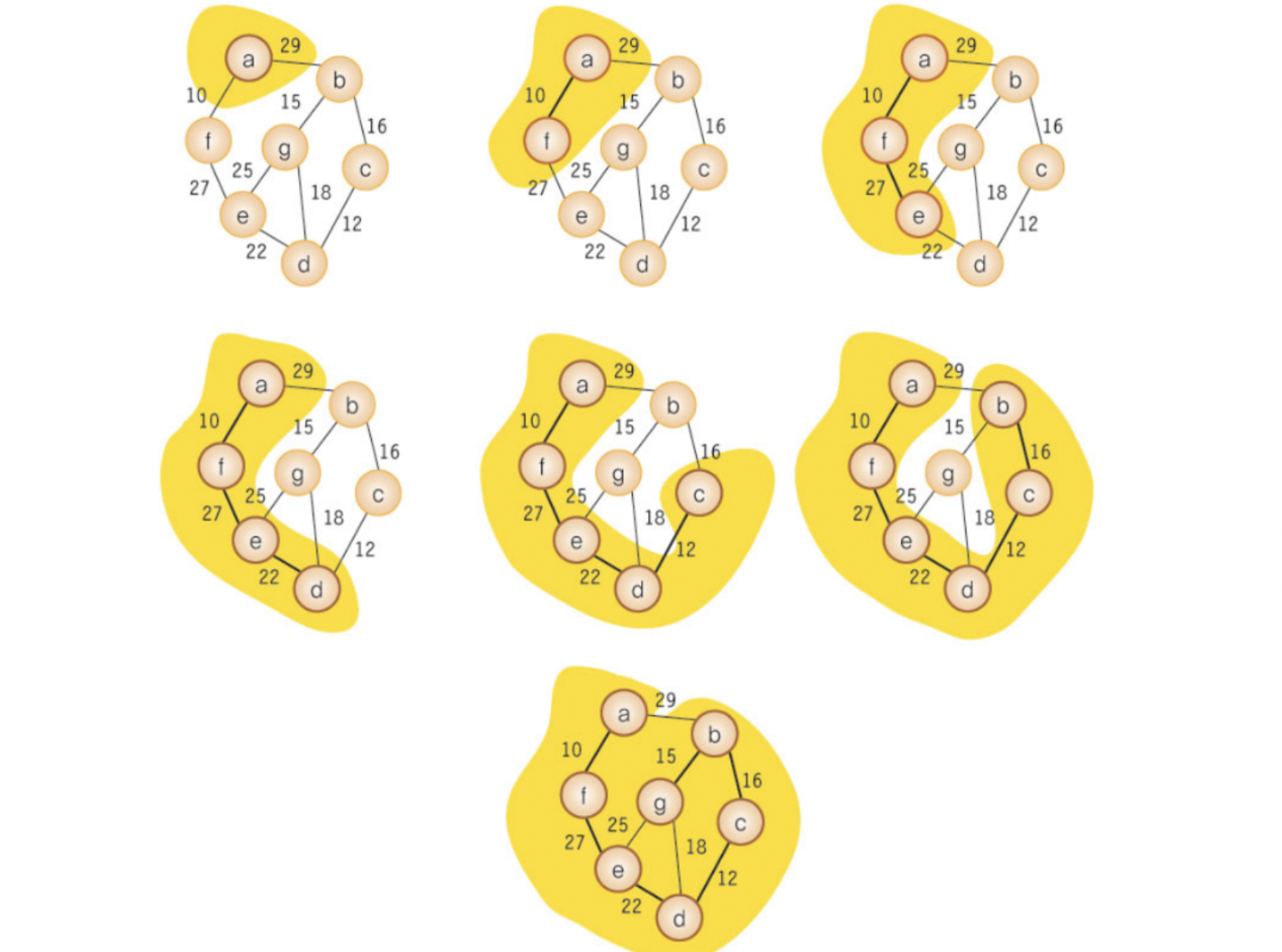
알고리즘 동작 과정
- 각 단게에서 사이클을 이루지 않는 최소 비용 간선을 선택
- 그래프의 간선들을 가중치의 오름차순으로 정렬되어 있다고 가정.
- 정렬된 간선 중에서 사이클을 형성하지 않는 간선을 현재 MST 집합에 추가
- 만약 사이클을 형성하면 그 간선은 제외
- Kruskal MST 알고리즘은 최적의 해답 임이 증명되었다.
동작 그림
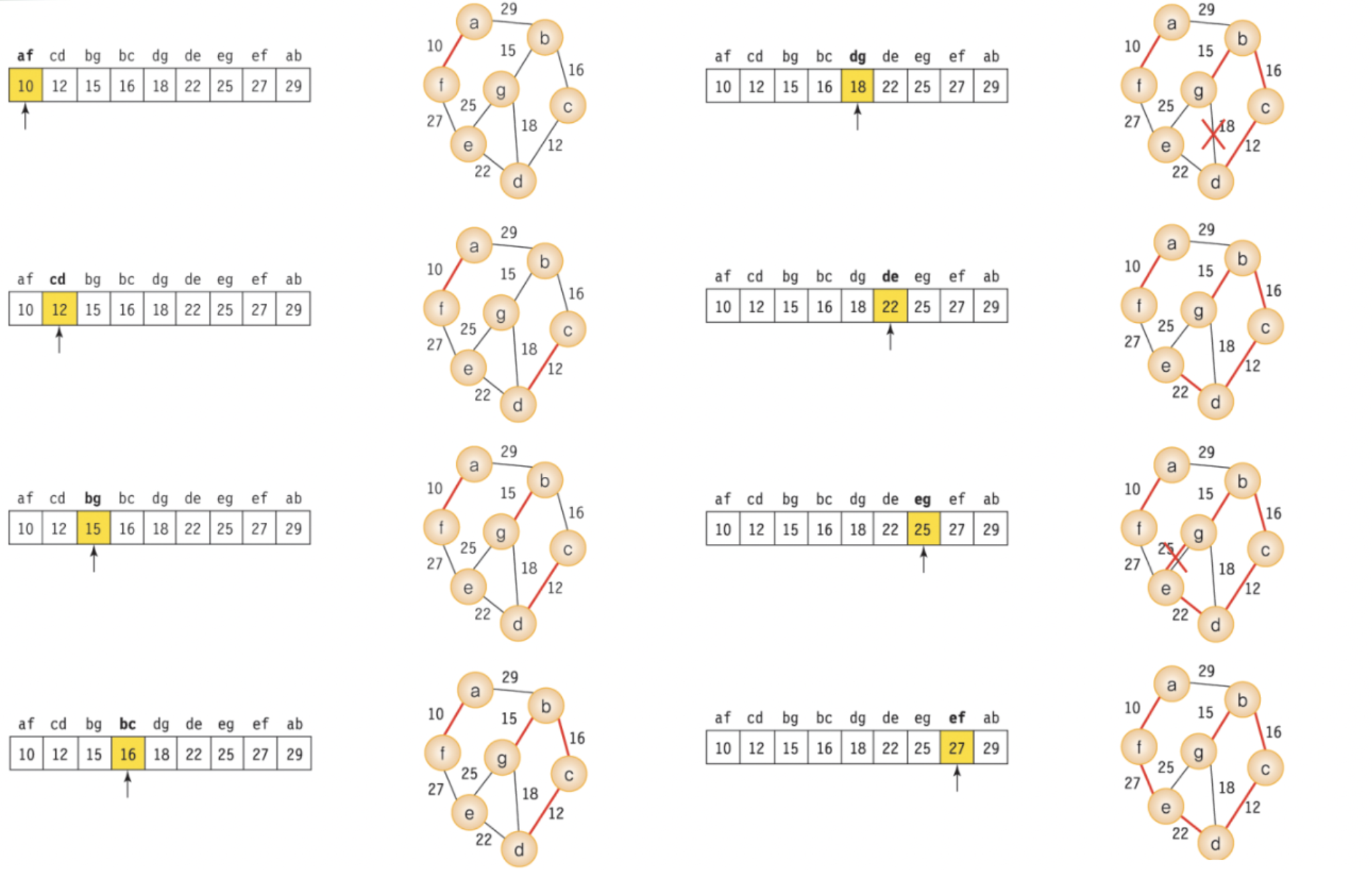
Kruskal의 MST 구현
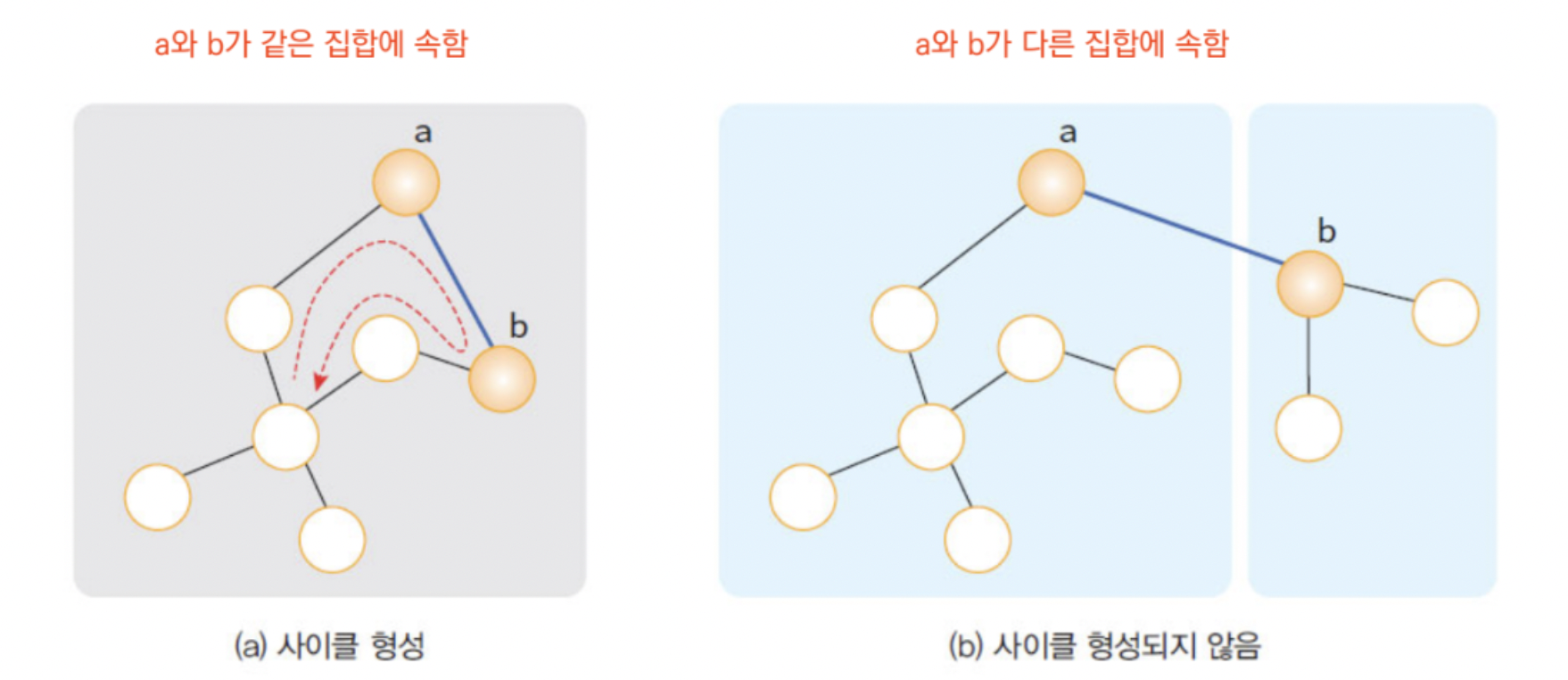
- union-find 알고리즘 : 두 집합들의 합집합
- 원소가 어떤 집합에 속하는지 알아낸다.
- Kruskal의 MST 알고리즘에서 사이클 검사에 사용된다.
C언어로 구현된 코드를 보고 싶다면 링크를 클릭하자.
Prim의 MST 알고리즘
- 동작 방식
- 시작 정점에서부터 출발하여 신장 트리 집합을 단계적으로 확장해 나간다.
- 시작 단계에서는 시작 정점만이 신장 트리 집합에 포함된다.
- 신장 트리 집합에 인접한 정점 중, 최저 간선으로 연결된 정점 선택하여 신장 트리 집합에 추가.
- 이 과정을 신장 트리 집합이 n-1개의 간선을 가질 때까지 반복한다.
- 시작 정점에서부터 출발하여 신장 트리 집합을 단계적으로 확장해 나간다.
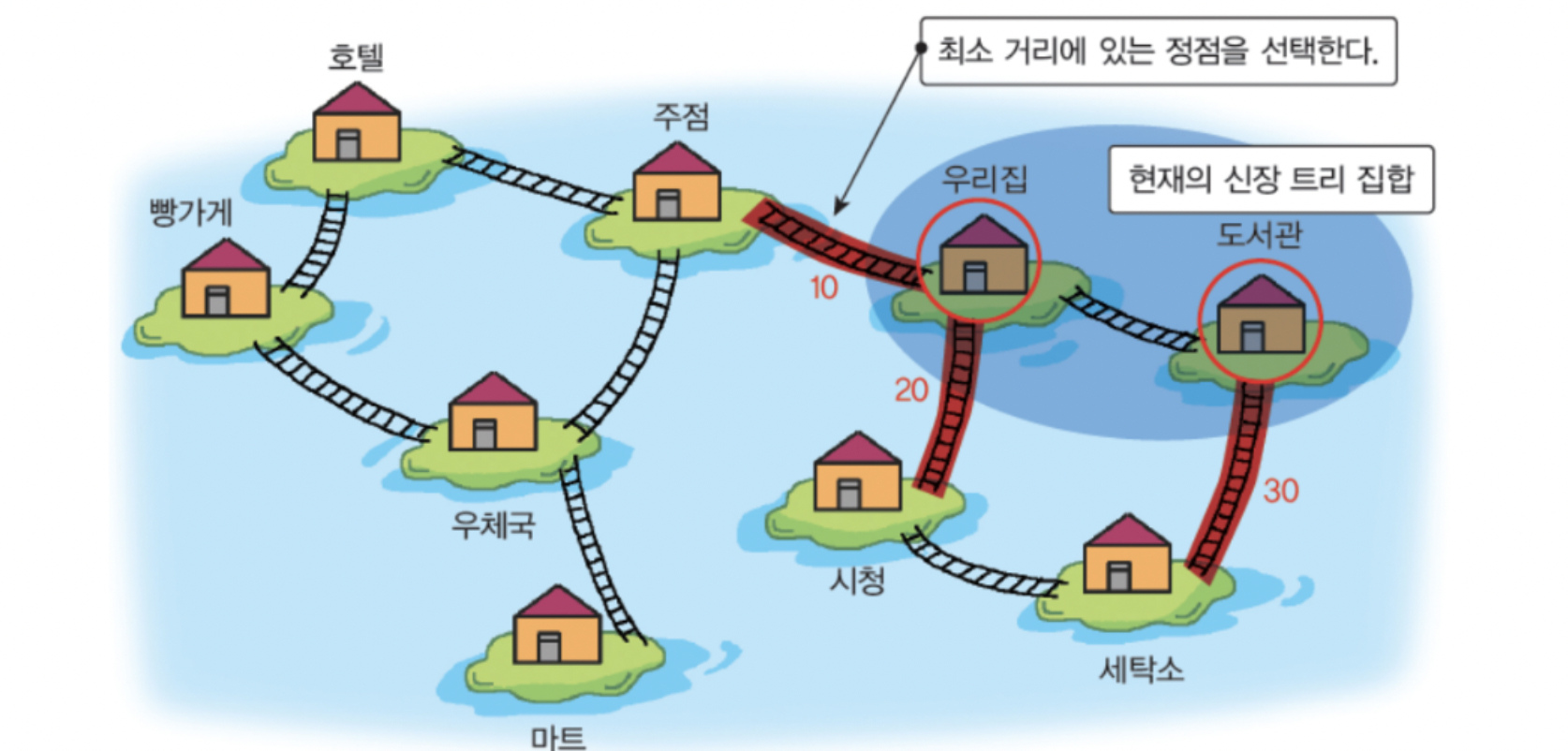
동작 그림
C언어로 구현된 코드를 보고 싶다면 링크를 클릭하자.
알고리즘 복잡도 비교
- Kruskal의 MST
- 대부분 간선들을 정렬하는 시간에 좌우된다.
- 사이클 테스트 등의 작업은 정렬에 비해 매우 신속하게 수행
- 네트워크의 간선 e개를 퀵 정렬과 같은 효율적인 알고리즘으로 정렬한다면
- Kruskal 알고리즘의 시간 복잡도는 O(e * log e)가 된다.
- 대부분 간선들을 정렬하는 시간에 좌우된다.
- Prim의 MST
- 주 반복문이 정점의 수 n만큼 반복하고, 내부 반복문이 n번 반복하므로
- Prim의 알고리즘은 O(n^2)의 복잡도를 가진다.
- 주 반복문이 정점의 수 n만큼 반복하고, 내부 반복문이 n번 반복하므로
따라서 희박한 그래프에서는 시간 복잡도가 O(e * log e)인 Kruskal 알고리즘이 유리하고,
밀집한 그래프에서는 시간 복잡도가 O(n^2)인 Prim 알고리즘이 유리하다.
