오늘은 분할정복 알고리즘과 다이나믹 프로그래밍에 대해 알아보고 실제로 그 둘의 공통점과 차이점에 대해서도 공부해보려고 합니다.
분할정복 알고리즘
분할정복(Divide and Concquer) 알고리즘은 그대로 해결할 수 없는 문제를 작은 문제 단위로 쪼개면서 해결하는 방법입니다. 분할정복 알고리즘의 설계 방식은 Divide, Conquer, Combine으로 나뉘어서 설계를 합니다.
- Divide : 원래 문제들을 비슷한 유형의 작은 문제들로 분할합니다.
- Conquer : 각 하위 문제들을 나눌 수 없는 단위가 될때까지 재귀적으로 해결합니다.
- Combine : 정복한 문제들을 통합하여 원래의 답을 해결합니다.
보통 분할정복 알고리즘에는 효율성을 위해 재귀(Recursion)이 사용되는 경우가 많습니다. 하지만 문제 해결 코드 작성 효율성 측면도 있지만 많은 재귀함수가 오히려 오버헤드를 야기시킬 수 있다는 것도 배제해서는 안됩니다.
정렬 알고리즘 비교
분할정복 알고리즘은 Quick Sort, Merge Sort, Binary Search, 선택 문제, 고속 푸리에 변환(FFT) 가 가장 대표적인데요. 그 중에서 퀵 정렬과 병합 정렬은 비슷한 것 같으면서도 차이점을 가지고 있는 알고리즘입니다.
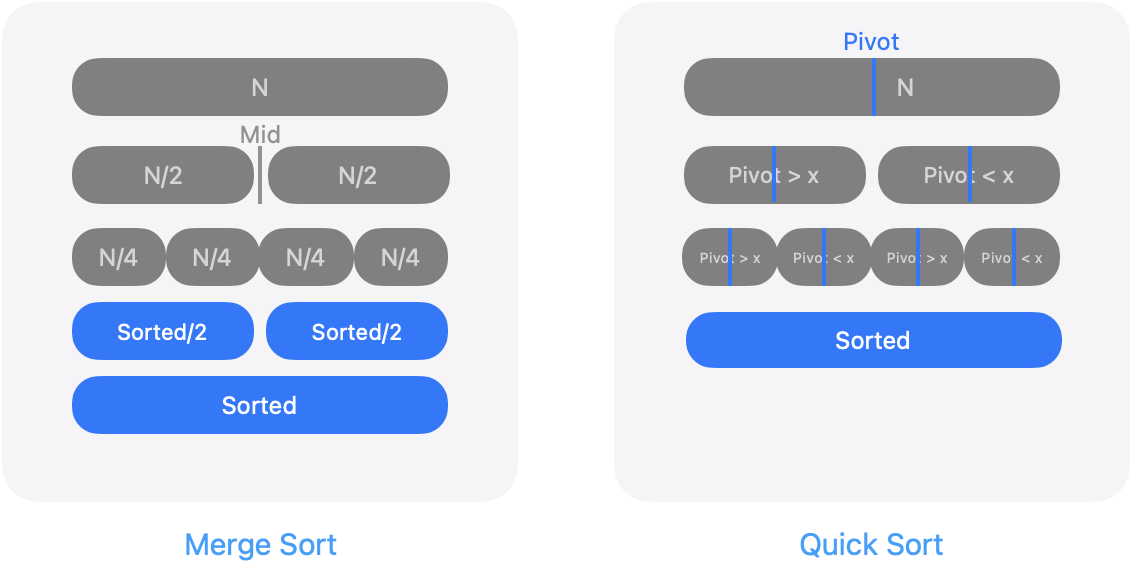
Merge Sort
- Divide : 하나의 배열을 두개의 작은 배열로 나눕니다.
- Conquer : 두개의 작은 배열이 최소화가 되었다면 정렬을 진행합니다.
- Combine : 정렬된 두개의 배열들을 하나로 통합합니다.
시간복잡도는 입니다. Concquer 과정에서 두개의 작은 배열들을 비교해 정렬을 진행하는데요. 이때, A의 모든 값이 B의 모든 값보다 작은 경우 모든 값들을 비교연산 할 필요 없다는 장점이 있습니다.
def merge_sort(arr):
if len(arr) <= 1:
return arr
# 리스트를 반으로 나누기
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
# 1. divide #
# 나눈 리스트에 대해 재귀적으로 병합 정렬 수행
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)
# 정렬된 두 개의 리스트를 병합
return merge(left_half, right_half)
def merge(left, right):
merged = []
left_idx, right_idx = 0, 0
# 두 개의 리스트를 비교하면서 작은 값을 병합 리스트에 추가
# 2. Concquer, Combine #
while left_idx < len(left) and right_idx < len(right):
if left[left_idx] < right[right_idx]:
merged.append(left[left_idx])
left_idx += 1
else:
merged.append(right[right_idx])
right_idx += 1
# 남은 요소들을 병합 리스트에 추가
merged += left[left_idx:]
merged += right[right_idx:]
return merged
# 예시로 사용할 리스트
arr = [38, 27, 43, 3, 9, 82, 10]
# 병합 정렬 호출
sorted_arr = merge_sort(arr)
print("정렬된 리스트:", sorted_arr)
Quick Sort
특정 원소 피봇(pivot) 을 기준으로 배열을 나누고 각 부분을 퀵 정렬로 적용하는 방식입니다.
- Divide : 피봇을 하나 선택해 이를 기준으로 2개의 배열로 나눕니다.
- Conquer : 피봇을 기준으로 큰 값, 작은 값으로 나누어 왼쪽부터 오른쪽까지 교환합니다.
- Combine : 따로 결합하지는 않습니다.
병합 정렬과 다르게 퀵 정렬은 최악의 시간 복잡도가 가 나올 수 있습니다. 왜냐하면 피봇을 기준으로 하나하나 비교를 하기 때문에 N의 제곱이 나올 수 밖에 없습니다. 정렬 하고자 하는 배열 안에서 정렬이 일어나므로 따로 메모리 공간이 필요하지 않습니다. 단점으로는 나눌떄, 두 리스트의 길이가 서로 다르기 때문에 수행시간이 많이 일어날 수 있다는 단점이 있습니다.(불안정 정렬) 그래서 pivot의 값이 중요한 것이죠.
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2] # 피벗을 리스트 중간에 위치한 요소로 선택
left = [x for x in arr if x < pivot] # 피벗보다 작은 요소들
middle = [x for x in arr if x == pivot] # 피벗과 같은 요소들
right = [x for x in arr if x > pivot] # 피벗보다 큰 요소들
# 작은 요소들과 큰 요소들에 대해 재귀적으로 퀵 정렬을 수행하고,
# 중간에 위치한 요소들은 그대로 두어 정렬을 완성
return quick_sort(left) + middle + quick_sort(right)
# 예시로 사용할 리스트
arr = [38, 27, 43, 3, 9, 82, 10]
# 퀵 정렬 호출
sorted_arr = quick_sort(arr)
print("정렬된 리스트:", sorted_arr)
퀵 정렬은 추가 메모리 공간이 필요없는 정렬입니다. 그러므로 cache의 지역성 때문에 병합 정렬보다 속도가 빠르다는 것을 알 수 있습니다.
[스택오버플로우] 퀵정렬이 어떻게 캐시와 연관이 있을까?
💡 퀵소트(Quick Sort)와 머지소트(Merge Sort)의 차이점
앞에서 보셨듯이, 같은 분할정복 알고리즘이지만 차이가 있습니다. 퀵정렬은 피벗을 기준으로 리스트를 분할하기 때문에 피벗의 값이 최소값이나 최대값가 가까우면 최악의 경우가 되어버릴 수 있다는 단점이 있습니다. 그리고 병합정렬은 매번 리스트를 분할하기 때문에 메모리 공간을 사용합니다. 반면, 정복 후에는 각 리스트들이 정렬되어 있기 때문에 순차적인 비교가 가능합니다. 만약header부터 탐색해야하는 연결리스트에 접근해야한다면 좋은 성능을 낼 수 있습니다.
동적 계획법
동적 계획법(Dynamic Programming)은 Optimal SubStructure의 효과를 발휘하는 방법입니다. 반복하기 위해 메모리 공간을 사용해 연산 속도를 증가시킵니다. 이러한 동적 계획법을 구현하기 위해 두가지 방식을 사용합니다.
💡 Optimal SubStructure
답을 구하기 위해 같은 방식의 계산을 반복하는 구조입니다. 같은 방식을 이전에 구해둔 풀이 방식을 사용하는 건데요. 이 규칙을 점화식으로 DP에 적용하는 것입니다.
💡 "동적"이라는 의미의 차이
우리가 흔하게 접했던 동적 할당(Dynamic Allocation)은 실행 중 프로그램 실행에 필요한 메모리를 할당하는 기법입니다. 하지만 여기서다이나믹이 동적 계획법의다이나믹과는 다른 의미으로 유의해둡시다.
탑다운과 보텀업은 언제 사용하는게 좋을까?
Bottom-up
작은 문제부터 차근차근 답을 도출하는 방식으로 반복문을 사용합니다. 최하위의 답을 구한 다음에 점차 상위 문제로 풀어가는 방식입니다.
- 우선 작은 문제부터 푸는 방식이 해결하기 쉽습니다.
- 가독성이 떨어진다는 단점이 있습니다.
memo[1] = 1
memo[2] = 2
n = 99
# 메모를 채워가는 방식
for i in range(3, n+1):
memo[i] = memo[i - 1] + memo[i - 2]Top-down
큰 문제를 풀다가 풀리지 않으면 재귀함수를 호출해서 답을 도출하는 방식입니다.
- 가독성은 좋습니다.
- 코드 작성이 어렵다는 단점이 있습니다.
memo = [0] * 100 # 메모리에 메모할 공간 생성
def fibo(x):
# 문제를 푸되
if x == 1 or x == 2:
return 1
# 만약에 계산한 적이 있는 경우
if memo[x] != 0:
return memo[x]
memo[x] = fibo(x-1) + fibo(x-2)
return memo[x]
이 두가지 방식 중 언제 어떤 방식을 사용하는게 좋을 지 고민을 해봤을 것 같습니다. 효율성을 생각해봤을 때, Bottom-up이 좋지만 만약에 문제의 크기가 그렇게 크진 않고 잘풀리지 않는다면 Top-down 방식을 사용하는게 좋을 것입니다. 스택의 크기를 벗어나게 되지 않는 경우를 말합니다. 사실 나도 점화식을 구하는게 더 어렵기 때문에 재귀로 푸는게 더 많습니다.
💡 메모이제이션(Memoization)
메모이제이션은 값을 구하기 위해 이전에 계산된 값을 저장해 계산하지 않고 속도를 높이는 기술입니다. 문제를 재활용하는 것이죠.memo = [0] * 100 # 메모리에 메모할 공간 생성 memo[0] = 0 # 결과 값 미리 저장 memo[1] = 1
문제) 2 X N 타일링
가로 길이가 2이고 세로의 길이가 1인 직사각형모양의 타일이 있습니다. 이 직사각형 타일을 이용하여 세로의 길이가 2이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다. 타일을 채울 때는 다음과 같이 2가지 방법이 있습니다.
- 타일을 가로로 배치 하는 경우
- 타일을 세로로 배치 하는 경우
예를들어서 n이 7인 직사각형은 다음과 같이 채울 수 있습니다.
직사각형의 가로의 길이 n이 매개변수로 주어질 때, 이 직사각형을 채우는 방법의 수를 return 하는 solution 함수를 완성해주세요.

def solution(n):
answer = 0
memo = [0] * 60001
for i in range(3, n+1):
memo[1] = 1
memo[2] = 2
memo[3] = 3
memo[i] = (memo[i - 1] + memo[i - 2]) % 1000000007
return memo[i]
최장 증가 수열(LIS)
최장 증가 수열은 N개의 원소가 있는 배열 중 일부 원소를 골라내어 만든 수열 중에서 다음과 같은 조건을 만족하는 수열을 최장 증가 수열(Longest Increasing Subsequence)이라고 합니다.
- 각 원소가 이전 원소보다 크다. (이건 오름차순을 유지한다는 조건)
- 부분 수열의 길이가 가장 길다.
즉, 가장 긴 오름차순 부분 수열을 찾는 것입니다.
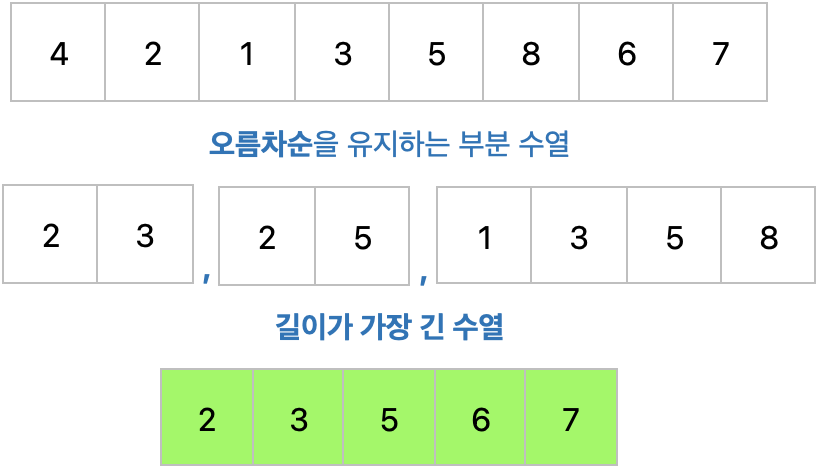
물론, 무조건 정답이 [2,3,5,6,7] 이라는 것은 아닙니다. [1,3,5,6,7] 도 될 수 있죠. 이처럼 LIS는 반드시 하나로 결정되는 것은 아닙니다.
왜 DP와 연관이 있을까?
LIS가 동작하기 위해 다이나믹 프로그래밍의 DP 테이블을 활용해 문제를 풀 수 있습니다. DP 테이블의 원소 값은 주어진 수열의 특정 값을 마지막 원소로 가지는 부분 수열의 최대 길이를 의미합니다. 그래서 초기에는 주어진 수열의 모든 값들이 1 로 초기화 합니다.
n = int(input()) # 수열의 길이
array = list(map(int, input().split())) # 수열
# Dp 테이블 초기화
dp = [1] * n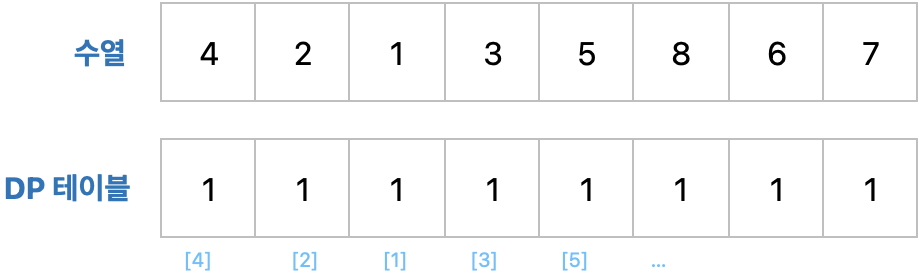
이제 수열의 두번째 값(2)부터 하나씩 확인해서 두번째 값(2)가 직전의 값들보다 크다면 DP 테이블에 두번째 값을 업데이트 합니다. 이때 점화식을 사용하게 되는데 DP 테이블의 두번째 값과 첫번째 값에 1을 더한 값 중 최대값을 업데이트 합니다.
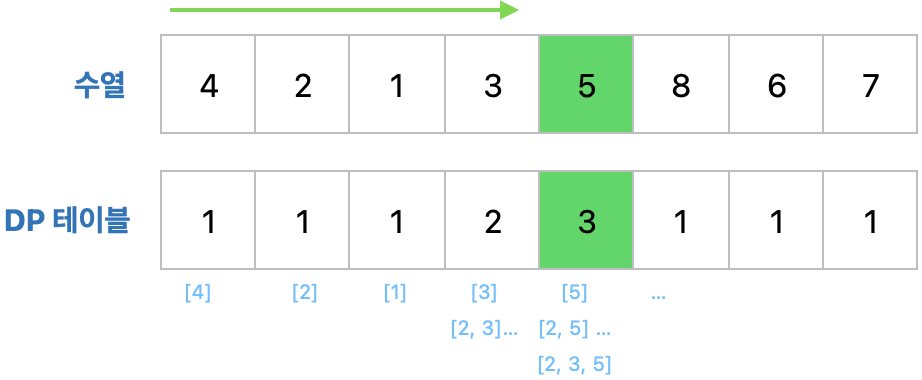
n = int(input()) # 수열의 길이
array = list(map(int, input().split())) # 수열
# Dp 테이블 초기화
dp = [1] * n
for i in range(1,n): # 현재 수열
for j in range(0, i): # 직전의 값들
if array[j] < array[i]:
dp[i] = max(dp[i], dp[j]+1)
# 가장 긴 증가하는 부분 수열의 길이
result = max(dp)따라서 위와 같은 과정을 반복해서 갱신하면 아래와 같은 DP 테이블이 최종 갱신됩니다.
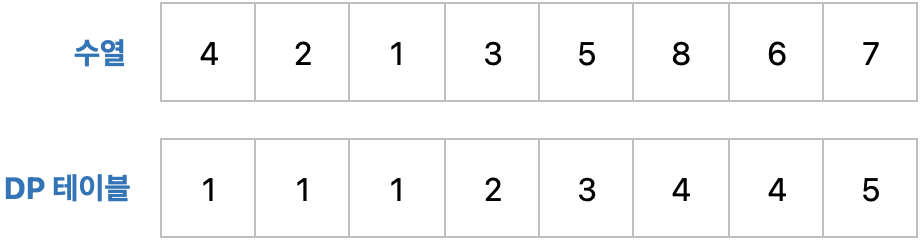
그러나, DP를 이용한 최장 증가 수열은 의 시간 복잡도를 갖습니다. 그래서 배열의 길이가 길다면 Lower Bound(으로 구현해야 합니다.
분할정복과 다이나믹 프로그래밍 차이
두 알고리즘은 문제를 작은 단위로 쪼갠다는 공통점이 존재합니다.
그러나 다만 차이점이 있다면, 다이나믹 프로그래밍은 문제들이 서로 영향을 미친다는 점(즉, 부분 문제들이 증복되어 재활용되는 DP와 다르게 분할 정복법은 서로 중복이 되지 않습니다.)입니다.
- 동적 계획법 : 부분 문제들이 서로 연결되어 있어 반복을 통해 문제를 해결한다. + Memoization을 사용한다.
- 분할 정복접 : 부분 문제들이 서로 독립적이다.
