투포인터와 슬라이딩 윈도우

DKf·2023년 9월 26일

Algorithm

목록 보기

7/9

오늘은, 슬라이딩 윈도우(Sliding Window) 와 투포인터(Two Pointer) 에 대해 공부해보려고 합니다. 이 둘의 공통점은 두가지 포인터를 이용해서 조건에 맞는 값을 찾는 알고리즘입니다. 하지만, 둘은 범위가 고정이 되어있냐, 아니냐에 따라 차이가 나는데요. 한번 자세히 알아보고 어떤 차이가 있는지 확인해 봅시다.

📌 슬라이딩 윈도우(Sliding Window)

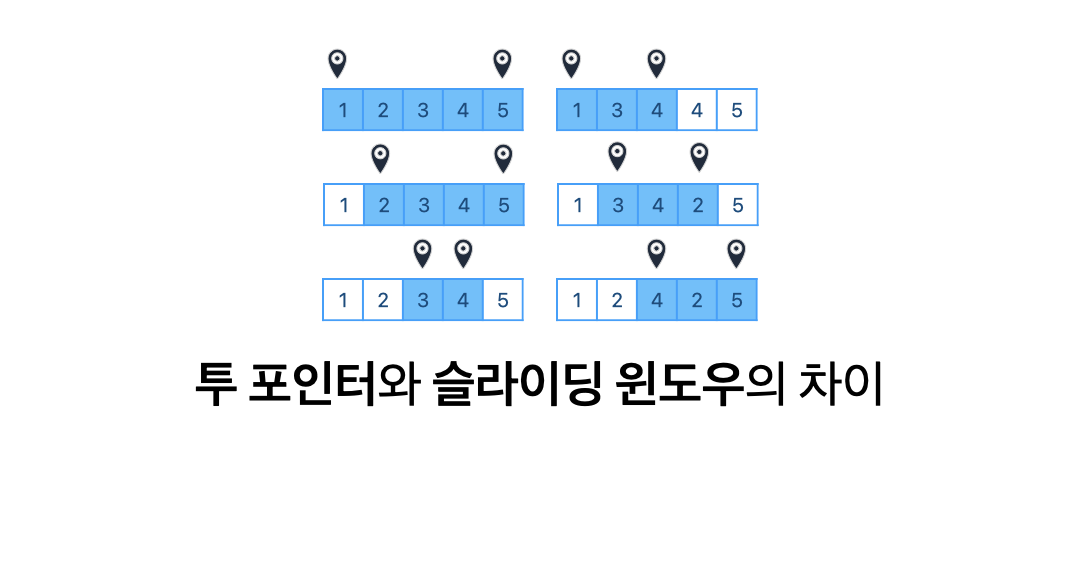
슬라이딩 윈도우는 일정한 길이의 범위를 이동하면서 조건에 맞는 값을 찾는 알고리즘입니다. 길이만 유지한채로 맨 앞, 맨 끝 원소만 갱신해나가는 방법입니다.

💡TCP에서 슬라이딩 윈도우
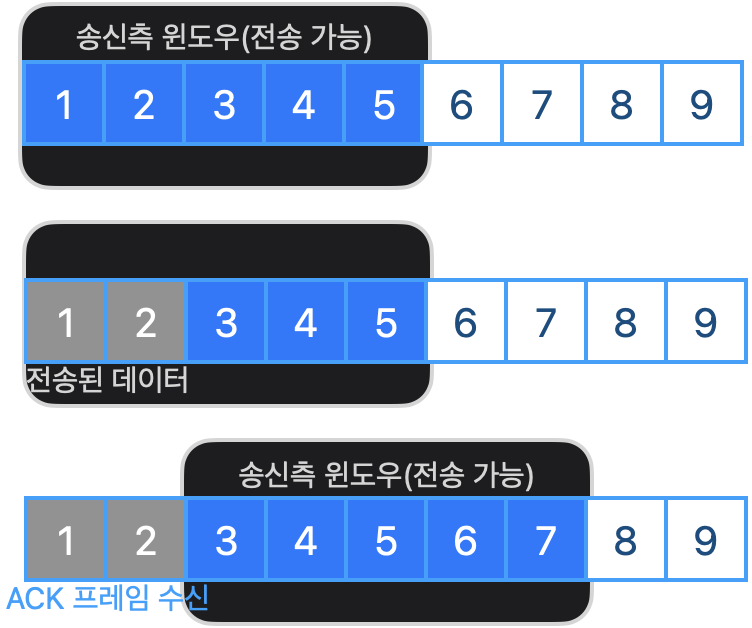
OSI 전송계층에서 데이터 전송의 흐름을 제어하기 위해 stop-and-wait과 슬라이딩 윈도우를 사용합니다. 이 중에서 슬라이딩 윈도우는 앞선 정지-대기 기법의 하나씩만 주고 받는다는 단점을 개선하기 위해 수신측에서 설정한 윈도우 크기 만큼 응답 없이 전송할 수 있는 구조입니다. 슬라이딩 윈도우에서 버퍼의 크기(윈도우 크기)가 존재하는데 고정된 크기 만큼 전송하게 되면 drop되는 패킷이 발생하지 않기 때문입니다.

TCP에서 슬라이딩 윈도우 처럼 슬라이딩 윈도우도 다음과 같습니다.

방금 위 구조를 예를 들어서 개념을 알아보겠습니다. 다음과 같은 배열의 구조가 존재한다고 했을 때, 연속적인 4개의 합이 최대값인 수를 구한다고 가정해봅시다. 맨 앞 원소 1이 빠지고 맨 뒤 원소 -1이 추가되는 것을 알 수 있습니다.

numbers = [1, 3, 2, 6, -1, 4, 1, 8, 2]
n = len(numbers)
k = 4 # 윈도우의 크기

window = sum(numbers[:k])
answer = window

for i in range(4, n):
    window += numbers[i] - numbers[i - k] # 맨 앞 원소 빼고 맨 뒤 원소 추가
    answer = max(window, answer) # 최대값 확인

문제 1) 최대 방문자 수 확인하기

백준 문제 보기 ＞

찬솔이가 블로그를 시작한지 N일이 지났다. 요즘 바빠서 관리를 못하고 있는데 벌써 6만이 넘었다.
찬솔이는 X일 동안 가장 많이 들어온 방문자 수와 기간을 알고 싶다 했을 때, 가장 많이 들어온 방문자 수와 기간을 구하시오.

입출력

풀이

n, m = map(int, input().split())
list = list(map(int, input().split()))

window = sum(list[:m])
answer = window
day = 1

for i in range(m, n):
    window += list[i] - list[i - m] # 맨 앞 원소 빼고 맨 뒤 원소 추가
    if window > answer:
        day = 1
        answer = window
    elif window == answer:
        day += 1



if answer == 0:
    print("SAD")
else:
    print(answer, day)

📌 투 포인터(Two Pointer)

말그대로, 두가지 포인터를 이용해 원하는 값을 찾을 때 쓰는 알고리즘입니다. 슬라이딩 윈도우와 다르게, 범위의 길이가 유동적으로 변한다는 차이가 있습니다.

투포인터에는 두가지 방법이 존재합니다.

특정 합을 가지는 연속 수열 찾기

어떤 정수 리스트가 있을 때, 합이 5가 되는 수열을 어떻게 찾을 수 있을까?
이 문제의 키 포인트는 시작점이 이동할 경우 합이 감소하고 끝점이 이동하면 합이 증가하는 알고리즘입니다.

백준 문제 보기 ＞

count = 0
interval_sum = 0 # 현재 부분합
end = 0

for start in range(n):

    # 1. 현재 부분합이 특정합 M 과 같다면 카운팅합니다. 
    if interval_sum == m:
			count += 1
            
	# 2-1. 같지 않고 M 보다 작은 경우 end을 1 증가하고 
    # 2-2.M 보다 큰 경우는 start를  1 증가시킵니다.
	while interval_sum < m and end < n :
				interval_sum += data[end]
				end += 1
		
	interval_sum -= data[start]

두 리스트를 하나의 리스트로 정렬하기

정렬된 두 리스트를 하나의 리스트로 합쳐 정렬된 리스트로 결과를 내는 방식입니다.
데이터 갯수가 n,m이라고 할때, 각 리스트의 데이터를 한번 씩 순회하기 때문에 $O(N+M)$ 입니다.

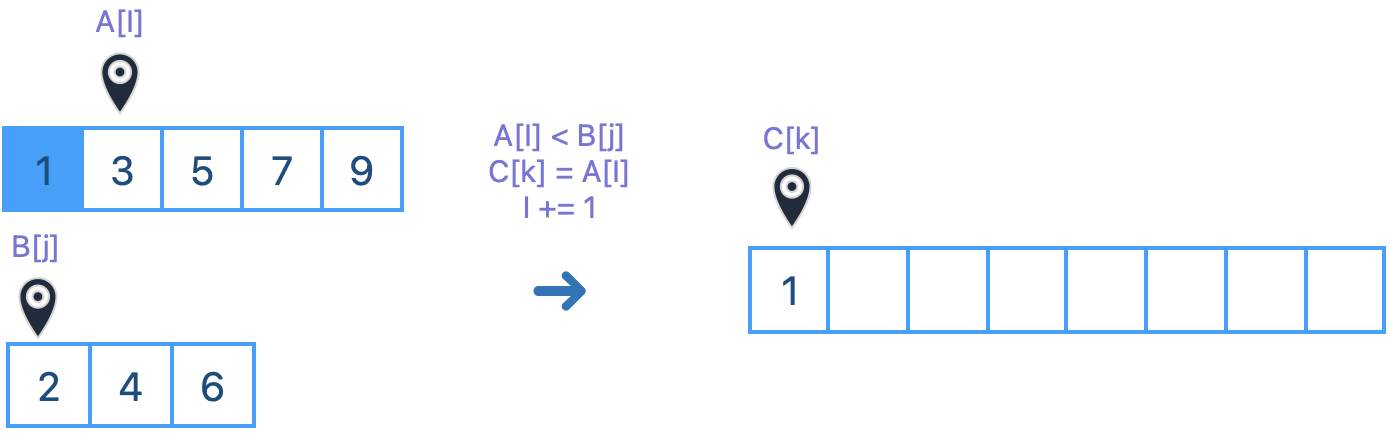
# 두 리스트 다 반복이 끝날때 까지
while i < n and j < m:
	# 1. 리스트 B의 원소(m)가 이미 다 처리 되었거나(j >=m) ⭐️
    # 2. 리스트 B의 원소가 작은 경우(while이 가능한 경우에서)
    if j >= m or (i < n and a[i] <= b[j]):
        result[k] = a[i]
		i += 1
        
	# 반대
	else:
		result[k] = a[j]
		j += 1

	k += 1

📌 누적합

범위의 합을 구하는 문제로 누적합을 구하는 문제가 있습니다. 누적합 문제는 연속적으로 나열된 N개의 수에서 특정 구간의 수들을 모두 합한 값을 구하는 문제인데요. 주로, 쿼리를 가정한 문제가 출제될 때가 많습니다.

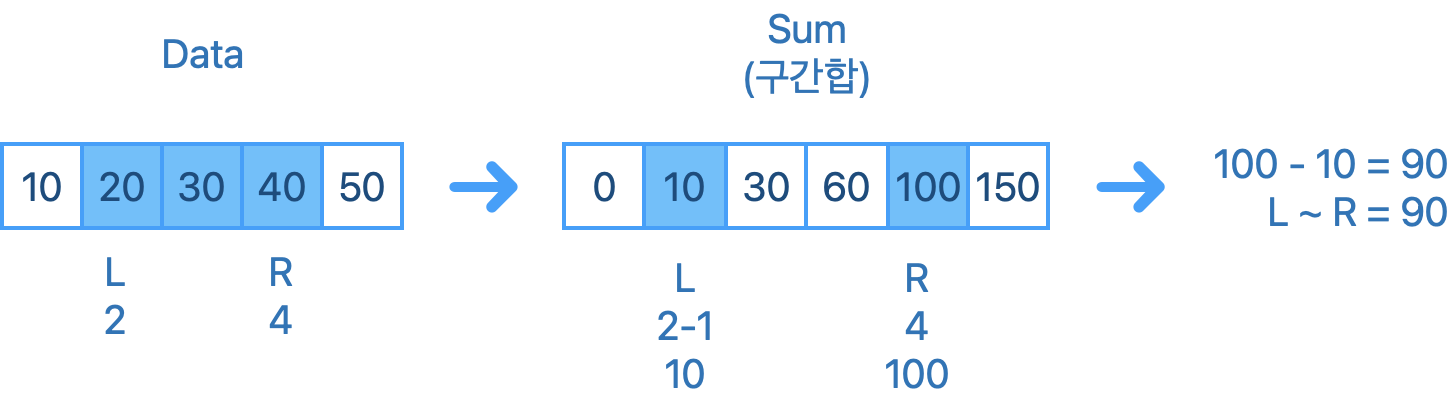
예를 들어, 다음과 같은 배열에서 20 ~50까지의 구간합을 구한다고 가정했을 때입니다.

n = 5
data = [10, 20, 30, 40, 50]

# Prefix Sum
sum_value = 0
prefix_sum = [0]

for i in data:
    sum_value += i
    prefix_sum.append(sum_value)

# result
left = 2
right = 4
print(prefix_sum[right] - prefix_sum[left-1])

DKf