[BOJ / Python] 11653 소인수분해

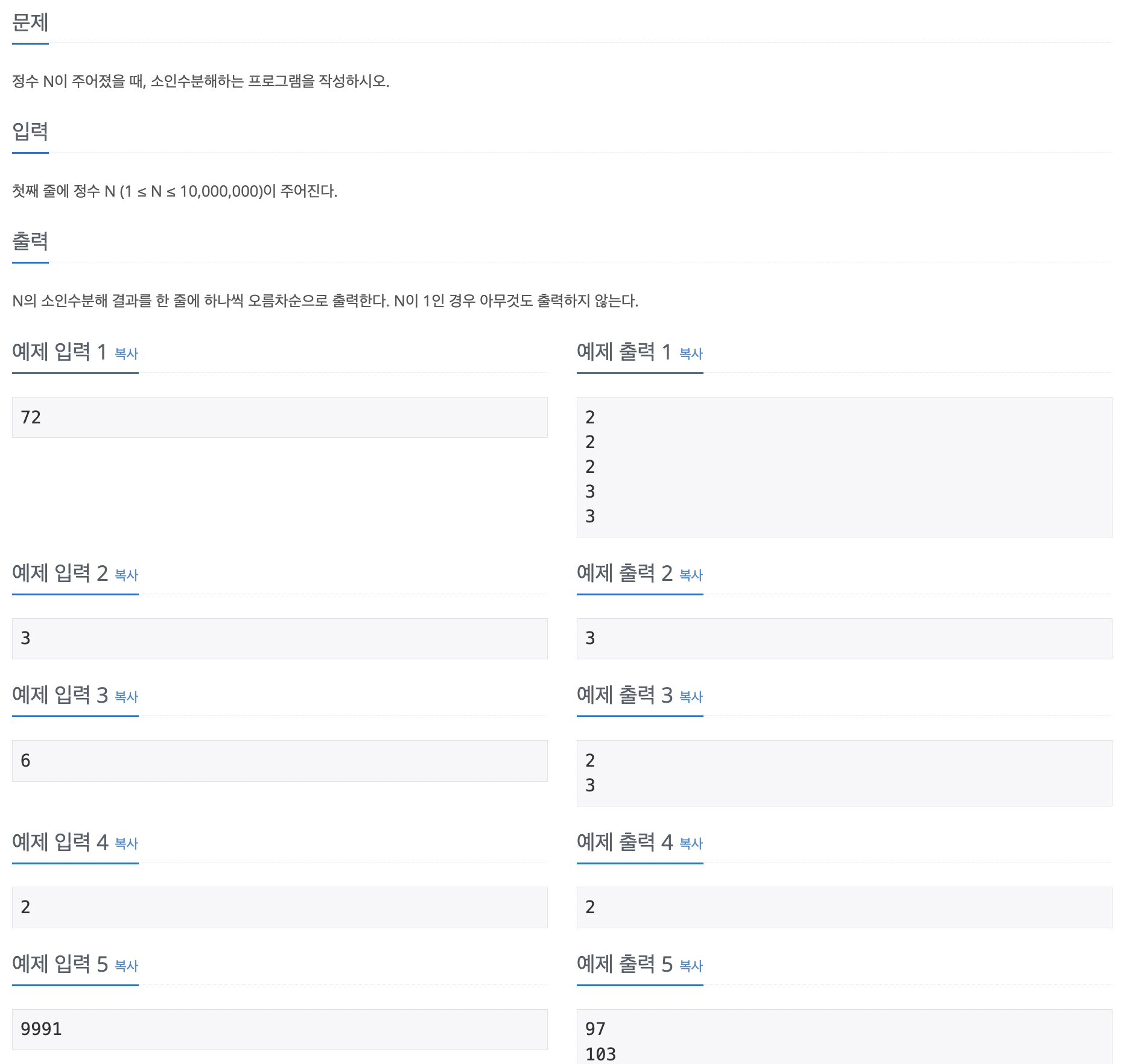
문제

백준 11653 소인수분해

코드

1. 부족한 코드

#BOJ 11653 소인수분해

n = int(input())
prime_num = []
if n == 1:
    print("")
else:
    for x in range(2, n+1):
        error = 0
        if x > 1:
            for i in range(2, x):
                if x % i == 0:
                    error += 1
            if error == 0:
                prime_num.append(x)

for y in prime_num:
    while n % y == 0:
        print(y)
        n = n / y

코드 설명
간단하게 위의 코드를 설명하자면, 1부터 n사이의 소수를 먼저 구한다. 이는 백준 1978 소수 찾기에서 작성한 코드와 유사하다. 구한 소수들을 리스트 prime_num 에 넣어두고 각각의 소수들에 대한 소인수분해를 진행한다.

Pycharm에서는 위의 코드가 돌아가긴 한다. 하지만 백준에 넣자 시간초과가 떴다.
for문과 while문이 너무 많은 탓이다.
위의 코드를 조금 더 간단하게 표현할 수 있는 방법은 없을까?

2. 더 나은 코드

#BOJ 11653 소인수분해

n = int(input())

if n == 1:
    print("")

for i in range(2, n+1):
    while n % i == 0:
        print(i)
        n = n / i

코드 설명
1번 코드에 비해 훨씬 더 간결해졌다.
1번 코드와 2번 코드의 가장 큰 차이는 소수를 저장하느냐 하지않느냐이다.

💡 작은 소수부터 나누어주면 소수가 아닌 수로 나누어지는 경우를 방지할 수 있다!

예를 들어, 72를 소인수분해한다고 해보자.
72 = 2 x 2 x 2 x 3 x 3 이다. 나는 72가 4, 8, ... 등 소수가 아닌 수들로 나누어지는 경우를 방지하기 위해 1번 코드에서 prime_num 리스트를 선언하고, 소수들을 저장하였다. 하지만, 소수를 작은 순서대로 나누어주면 소수가 아닌 수들로 나누어지는 경우를 방지할 수 있다. 72를 2로 가능한 한 여러 번 나누면 2 또는 2의 배수로 나눌 수 없는 수가 남는다.

72 / 2 = 36 → 36 / 2 = 18 → 18 / 2 = 9

따라서 입력값 n에 대한 소수를 모두 저장할 필요가 없다!
2부터 n까지의 수를 순서대로 나누어주면 된다. 단, 해당 숫자로 더 이상 나눌 수 없을 때까지 나누어주어야 하므로 while n % i ==0 을 이용하여 여러 번 나눌 수 있도록 한다.