[BOJ / Python] 24267 알고리즘 수업 - 알고리즘의 수행 시간6

문제

백준 24267 알고리즘 수업 - 알고리즘의 수행 시간6

코드

#BOJ 24267 알고리즘 수업 - 알고리즘의 수행 시간6

n = int(input())
print(int((n-2)*(n-1)*n/6))
print(3)

코드 설명
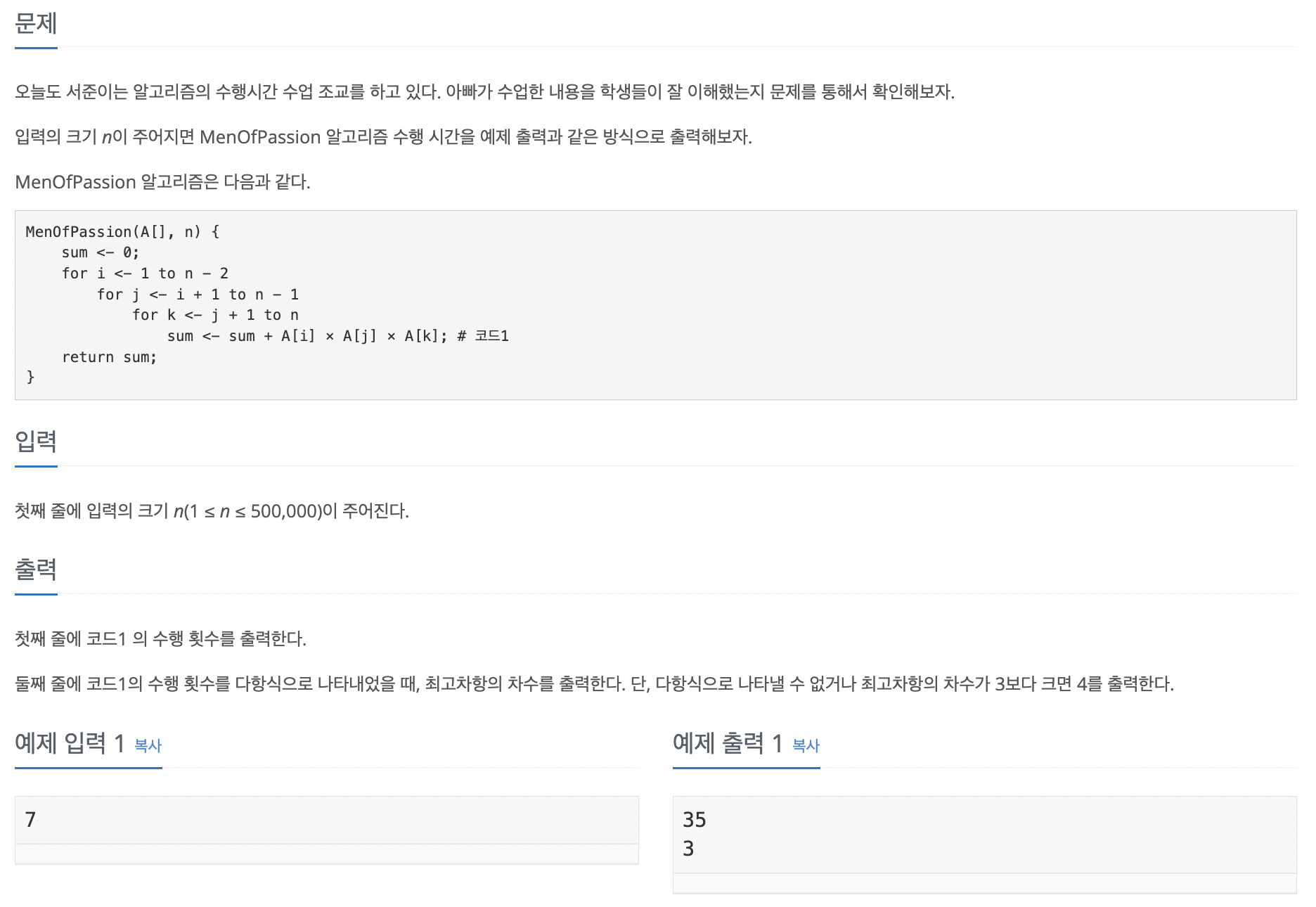
코드 1, sum <- sum + A[i] x A[j] x A[k]이 세 개의 for문 안에 들어있다.
첫 번째 for문은 1부터 n-2까지, 두 번째 for문은 i+1부터 n-1까지, 세 번째 for문은 j+1부터 n까지 반복한다.

$\small \displaystyle \sum_{k=1}^{n-2}(\sum_{x=1}^{k}{x})=\sum_{k=1}^{n-2}(\frac {k\times (k+1)}2) = \sum_{k=1}^{n-2}(\frac{1}{2}(k^2 + k)) = \frac{1}{2}(\sum_{k=1}^{n-2} k^2 + \sum_{k=1}^{n-2} k) \\ = \frac{1}{2}\{ \frac{(n-2)(n-1)(2n-3)}6 + \frac{(n-2)(n-1)}{2} \} \\ = \frac{(n-2)(n-1)}{4} ( \frac{2n-3}{3} + 1 ) \\ = \frac{(n-2)(n-1)}{4} \times \frac{2n}{3} \\ = \frac{(n-2)(n-1)n}{6}$

즉, 총 수행횟수는 (n-2)*(n-1)*n/6 이다.
따라서 코드 1의 수행횟수는 (n-2)(n-1)n/6 번이고, 최고차항의 차수는 2이다.