.png)
🎄 트리의 구현과 순회
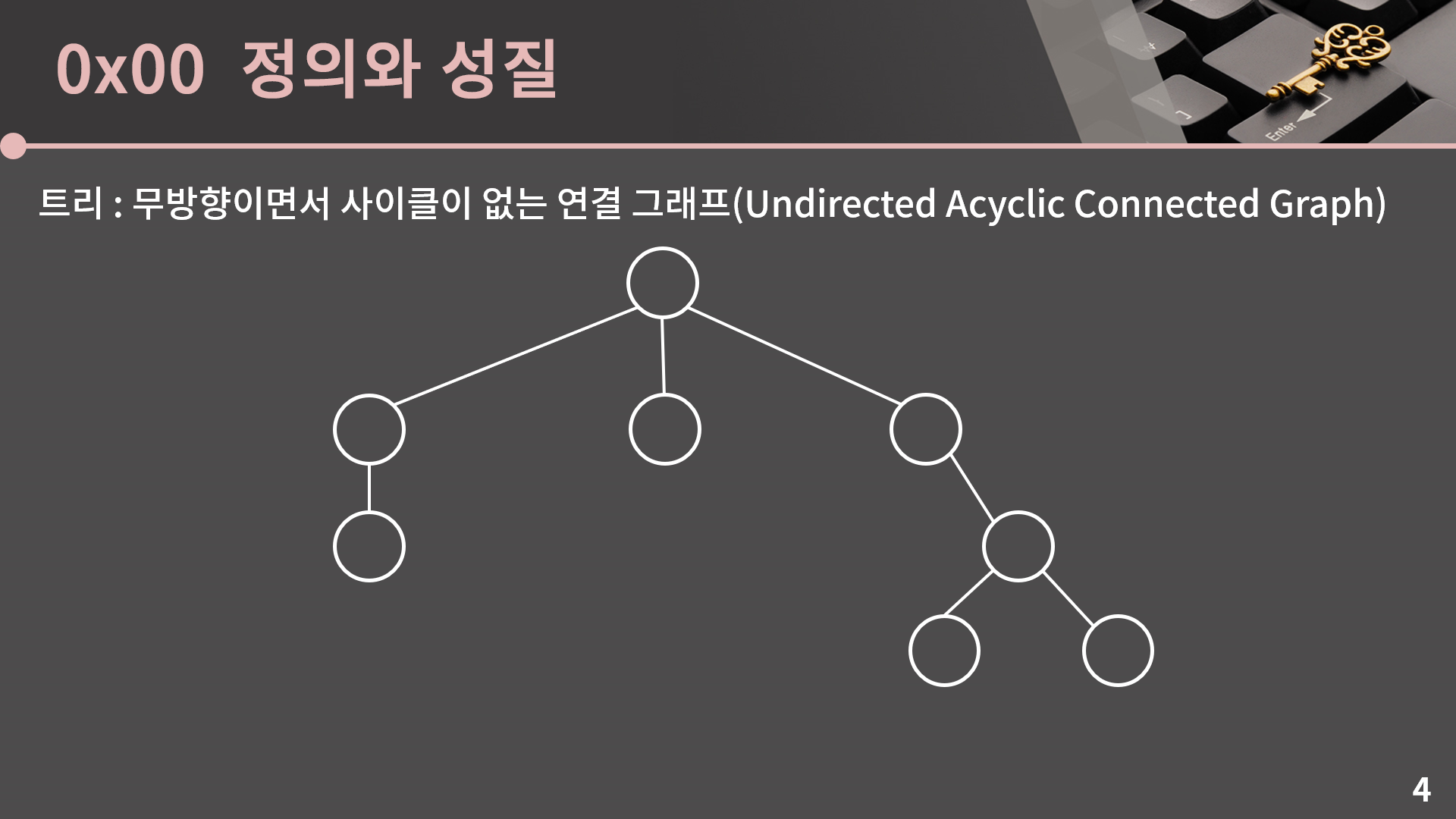

계층 구조는 선형으로 표현하기 어려운 형태이다. 자료 간에 상하위 관계나 포함 관계가 존재하는 경우 계층 구조가 생긴다.
이렇게 계층적 구조를 갖는 자료들을 표현하기 위한 자료구조가 바로 트리(Tree)이다.
특정한 조건을 지키도록 구성된 트리들을 이용하면 배열이나 리스트를 사용하는 것보다 같은 작업을 더 빠르게 구현할 수 있다.
1️⃣ 기초적인 정의와 용어
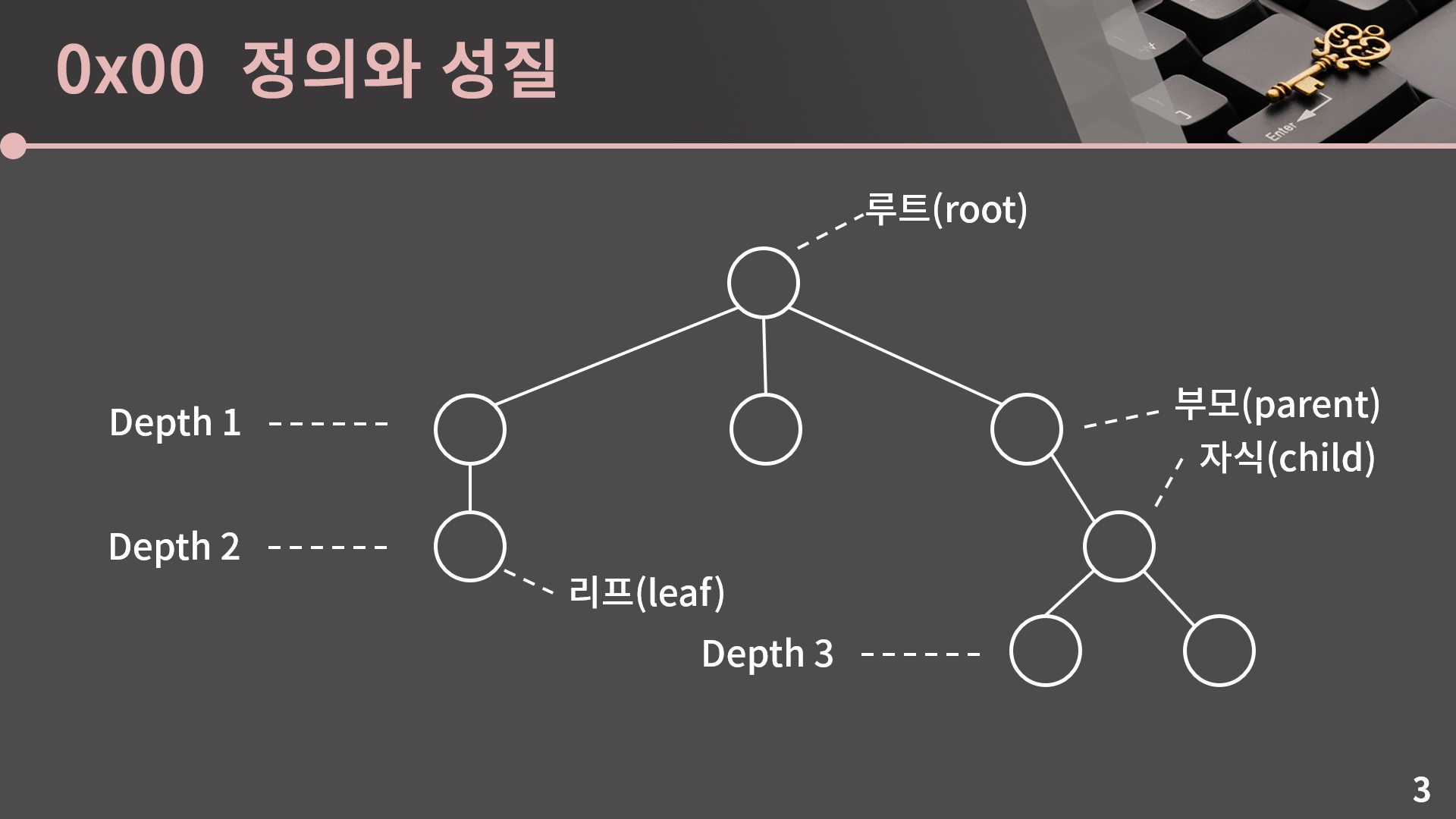
- 트리의 구성 요소 트리는 자료가 저장된
노드(node)들이간선(edge)으로 서로 연결되어 있는 자료 구조를 말한다.
노드 간에는 상/하위 관계가 있으며, 두 노드가 연결되었을 때 한 노드는 상위, 다른 노드는 하위에 있어야 한다. 두 연결된 노드 중 상위 노드를부모(parent), 하위 노드를자식(child)노드라고 부른다.
부모 노드가 같은 두 노드는형제(sibiling)노드라고 부른다.
부모 노드와 그의 부모들을 통틀어선조(ancestor)라고 부르고, 자식 노드와 그의 자식들을 통틀어자손(descendant)이라고 부른다. 트리에는 최상단에 다른 모든 노드들을 자손으로 갖는 노드가 딱 하나 있게 된다. 이 노드를 트리의 뿌리 노드 혹은루트(root)라고 부른다.
반대로 최하단에 자식이 하나도 없는 노드들을 트리의 잎 노드 혹은리프(leaf)라고 부른다.
- 트리와 노드의 속성 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수를 해당 노드의
깊이(depth)라고 한다.
따라서 깊이가 깊을수록 트리 아래쪽에 있는 노드를 지칭하게 된다.
이때 트리에서 가장 깊숙히 있는 노드의 깊이를 해당 트리의높이(height)라고 한다.
- 트리의 재귀적 속성 트리가 유용하게 사용되는 큰 이유중 하나는 트리가 재귀적인 성질을 갖고있기 때문이다.
트리에서 한 노드와 그의 자손들을 모두 모으면 그들도 하나의 트리가 된다.
이때 어떤 노드 t와 그 자손들로 구성된 트리를‘t를 루트로 하는 서브트리(subtree)’라고 말한다. 따라서 모든 트리는 루트와 루트 밑에 있는 서브트리들의 집합이라고 말할 수 있다.
이와 같은 재귀적 속성 때문에 트리를 다루는 코드들은 대개 재귀 호출을 이용해 구현된다.
- 트리의 표현 트리는 다양한 방법으로 구현할 수 있다.
그중 가장 일반적인 형태는 각 노드를 하나의 구조체/객체로 표현하고, 이들을 서로의 포인터로 연결하는 것이다.
이때 각 노드들은 자신의 부모와 모든 자손들에 대한 포인터를 가지고 있다. 이런 방식으로 트리를 표현할 때 사용하는 노드 객체의 간단한 구현 코드이다.struct Tree Node{ string label; //저장할 자료 TreeNode* parent; // 부모 노드를 가리키는 포인터 vector<TreeNode*> children; // 자손 노드들을 가리키는 포인터의 배열 }
- 트리의 특징 정리
- 하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 있다.
- 데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조이다
- 트리 내에 또 다른 트리가 있는 재귀적 자료구조이다.
- 단순 순환(Loop)을 갖지 않고, 연결된 무방향 그래프 구조이다.
- 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 갖는다.
- 노드가 n개인 트리는 항상 n-1개의 간선(edge)을 가진다.
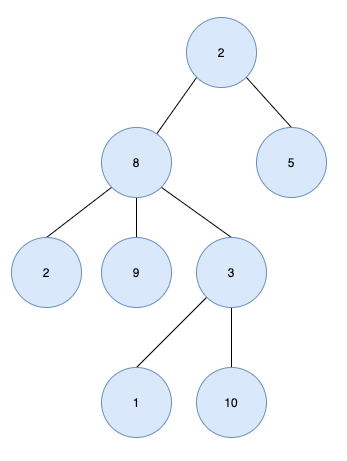
- 트리가 아닌 경우
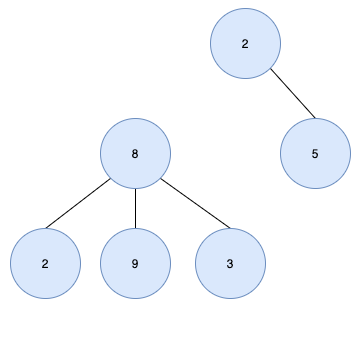 루트 노드가 2개(2, 8) 있으므로 트리가 아니다.
루트 노드가 2개(2, 8) 있으므로 트리가 아니다. 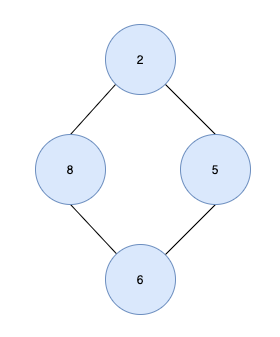 노드 6에는 2명의 부모 노드(8,5)가 있고 사이클(2-8-6-5)이 형성되므로 트리가 아니다.
노드 6에는 2명의 부모 노드(8,5)가 있고 사이클(2-8-6-5)이 형성되므로 트리가 아니다.
2️⃣ 트리 종류
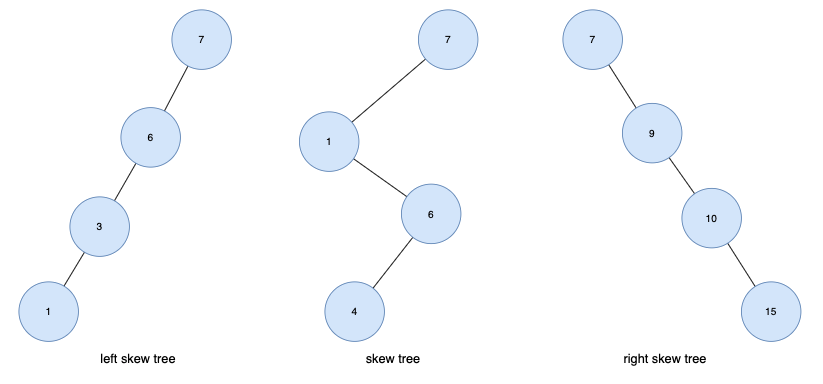
편향 트리(Skew Tree)
- 모든 노드들이 자식을 하나만 가진 트리
- 왼쪽 방향으로 자식을 하나씩만 가질 때 left skew tree, 오른쪽 방향으로 하나씩만 가질 때 right skew tree라고 함.
이진트리 (Binary Tree)
- 각 노드의 차수(자식 노드)가 2 이하인 트리
이진 탐색 트리 (Binary Search Tree, BST)
- 순서화된 이진 트리
- 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 함.
m-원 탐색 트리(M-way Search tree)
- 최대 m개의 서브 트리를 갖는 탐색 트리
- 이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용함.
균형 트리 (Balanced Tree, B-Tree)
- m원 탐색 트리에서 높이 균형을 유지하는 트리
- height-balanced m-way tree라고도 함.
3️⃣ 사용 사례
- 계층적 데이터 저장
- 트리는 데이터를 계층 구조로 저장하는 데 사용된다.
- 예를 들어 파일 및 폴더는 계층적 트리 형태로 저장된다.
- 효율적인 검색 속도
- 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용한다.
- 힙(Heap)
- 힙도 트리로 된 자료 구조이다.
- 데이터 베이스 인덱싱
- 데이터베이스 인덱싱을 구현하는데 트리를 사용한다.
- 예) B-Tree, B+Tree, AVL-Tree..
- Trie
- 사전을 저장하는 데 사용되는 특별한 종류의 트리이다.
4️⃣ 트리의 순회
모든 트리는 각 자식들을 루트로 하는 서브트리와 루트로 나눌 수 있으므로, 트리의 루트가 주어질 때 루트를 ‘방문’한 뒤 각 서브트리를 재귀적으로 방문하는 함수를 만들어 트리의 모든 노드를 순회할 수 있다.
//트리를 순회하며 모든 노드에 포함된 값을 출력하기
//주어진 트리의 각 노드에 저장된 값을 모두 출력한다.
void printLabels(TreeNode* root) {
//루트에 저장된 값을 출력한다.
cout << root -> label << endl;
//각 자손들을 루트로 하는 서브트리에 포함된 값들을 재귀적으로 출력한다.
for(int i = 0; i< root -> children.size(); ++i)
printLabels(root->children[i]);
}- 트리의 높이를 구하는 문제
서브트리의 개념을 이용하면 트리의 높이 또한 재귀적으로 정의할 수 있다.
루트의 각 자식들을 루트로 하는 서브트리들의 높이를 각각 재귀 호출을 통해 계산하면 전체 트리의 높이는 그중 최대치에 1을 더한 것이 된다.
//순회를 이용해 트리의 높이를 계산하기
//root를 루트로 하는 트리의 높이를 구한다
int height(TreeNode* root){
int h = 0;
for(int i=0; i<root->children.size(); ++i)
h = max(h,1+height(root->children[i]));
return h;
}출처
https://yoongrammer.tistory.com/70?category=956616 yoongrammer 블로그
프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 2 - 구종만 지음
https://blog.encrypted.gg/1013?category=773649 바킹독 실전 알고리즘 이진트리
