Double DQN paper

Introduction

기존에 제시된 DQN 방식은 overestimation으로 인한 문제를 겪고 있는데 이를 해소한 것이 이 논문의 주 요지이다.
Overestimation이 진짜 문제가 되는지는 논란의 여지가 있는 open problem인데 전체적으로 value function 이 커진다면 그들 사이의 relative preference는 유지되기 때문에 큰 문제가 되지 않는다.
하지만 overestimation이 특정 state에 집중되어 있을 경우에는 policy의 성능에 영향을 미칠 것이다.
Overestimation이 practice에서 일어나는지 확인하기 위해 DQN 알고리즘을 이용해 테스트 한다. DQN은 Neural Network를 사용해 low asymptotic approximation error를 제공하고 게임 환경이 deterministic 하다는 점에서 Q -learning에 좋은 환경이라고 할 수 있지만 이러한 배경 속에서도 value의 overestimation이 관찰된다.
이번 논문에서는 Double Q-learning과 DNN을 합쳐 DDQN 알고리즘을 제시하고 결과적으로 더욱 accurate한 value estimation이 이뤄짐을 보인다. 이를 통해 overestimation이 지금까지 가하던 단점들을 지적한다.

Background

$\theta$로 parameterised 된 value function Q는 아래와 같이 update 될 수 있다

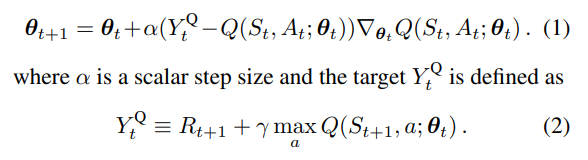
이 방식은 Least Square을 objective function으로 이를 최소화 하려는 방향으로 움직이고 싶을 때 취하는 SGD 방식이다.

DQN Recap
이 방식의 Q network는 input으로 n dimension 의 state vector를 받고 가능한 모든 action에 대한 m dimension의 output을 내놓는다
두가지 key idea는 target network와 experience replay 인데 이는 각각 every time step 마다 Target function의 parameter를 업데이트 하는 것이 아닌 고정 방식이고 후자는 memory 집합 D에 시퀀스들을 저장 후 sampling 해 사용한다는 것이다.

Double Q - Learning
기존 DQN에서는 action을 고르는 것과 evaluation 하는 데 같은 값을 쓴다는 단점이 있는데 이는 overoptimistic estimate를 일으키기 때문이다. 아래의 식을 통해 직관적으로 이해할 수 있다.

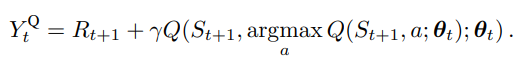
이러한 couple 관계를 깨 overestimation을 막는다는 것이 Double Q-learning의 아이디어 이며 Q network는 이제 $\theta, \theta'$ 두개의 parameter를 갖는다.
하나의 weight(parameter)는 greedy policy를 정하는데 사용되고 다른 하나는 value를 정하는데 사용된다.

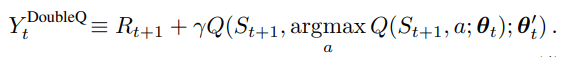
greedy policy를 정하는 것은 $\theta$, value를 정하는 것은 $\theta'$라고 이해할 수 있다.
위의 두 parameter 의 역할을 바꿔 symmetric update를 하는 것도 가능하다

Estimation error가 부르는 overoptimism
environment 에 있는 noise가 overestimation을 부른다는 논문이 소개되었음
이 장에서는 어떤 종류의 노이즈(function approximation, non-stationary, any other source)인가 상관없이 이들은 upward bias를 유도한다는 것을 보이려 한다.
이러한 탐구의 중요성은 실전에서 learning에 일어나는 inaccuracy는 무궁무진하기 때문이다
Thrun, Schwartz(1993)의 overestimation 상한 계산에서 더 나아가 lower bound를 구해보도록 하자

특정 가정) value estimate이 average 하게는 맞지만 아래와 같은 차이가 존재하는 경우
다음과 같은 lower bound가 존재한다.

위의 theorem이 명시하는 lower bound는 액션의 수가 증가할수록 감소한다

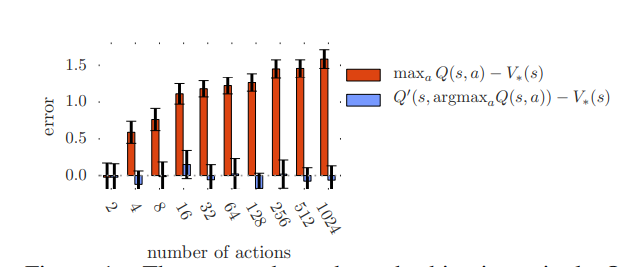
위의 도표에서 오렌지 색은 single Q-learning에서 overestimation 을 나타내며 action의 수가 증가할수록 같이 증가함을 확인할 수 있다. 하지만 파란색으로 표시된 double Q-learning은 (Q'과 Q 두개의 action value function 사용함을 확인가능) 액션 수에 unbiased 되어있다.

그 다음으로 집중할 것은 function approximation에 대한 것

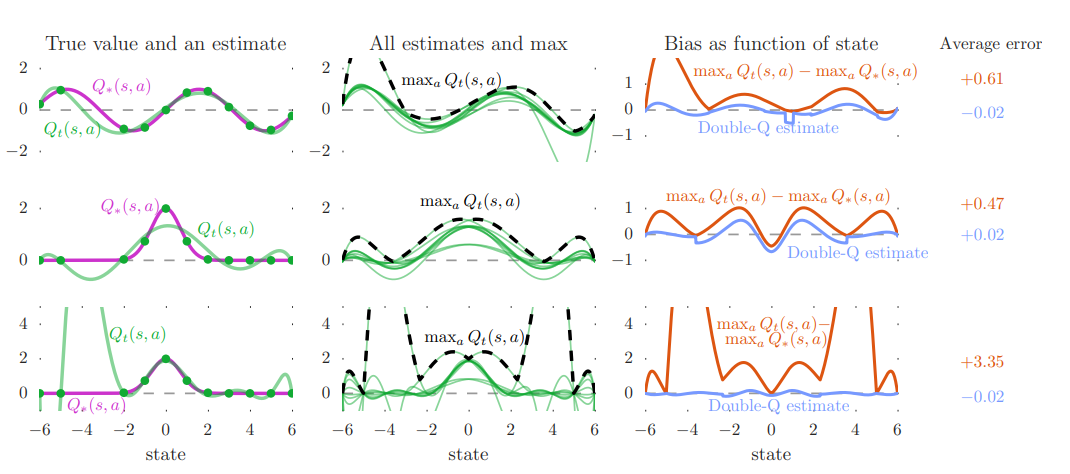
가장 좌측 column은 true value을 나타내며 green 선은 single action에 대해 value function estimation을 보이고 dot은 sample된 지점을 의미한다
1,2 줄의 estimation function 차수는 6이고 마지막 row의 차수는 9이다. 차수가 6인 경우 flexibility 가 떨어지기 때문에 sample 에서 조차 맞지 않는 현상을 보인다. 9차 function estimation은 sample 지점에서는 정확성이 높지만 unsampled state에서 정확도가 낮은 현상을 보인다. (이는 왼쪽에 sample 간격이 넓은 지점에서 큰 오차를 통해 확인가능하다)

두번째 column은 모든 10 action에 대해 estimation function 결과를 보이며(green) 검은 점선은 각 state에 대해 maximum action value 값을 보인다. 이 값은 왼쪽 column에 purple로 표시된 ground truth보다 높은 값을 보이곤 한다.
이 차이는 가장 오른쪽 column의 orange plot을 통해 확인할 수 있고 이를 통해 upward bias를 확인해볼 수 있다. 동시에 파란색으로 표시된 Double Q learning을 통한 estimation 값은 0에 가까이 논다는 사실을 확인할 수 있다.

위의 과정에서 sample 값은 true action value를 통해 얻어진 것인데 이는 실제 상황보다 optimistic 한 가정이다. 실제로는 bootstrapping을 통해 action value를 추정하고 이는 이미 overestimate 된 값을 기준으로 상상하는 것이기 때문에 overestimation이 전파된다고 이해할 수 있다.
좋은 방향으로 가정한 실험 환경의 결과도 overestimation이 심하다는 결론을 통해 실제로는 divergence를 고려할 만큼 심한 overestimation이 이뤄질 수 있고 각 state에 고르게 분포되어 upper biased 되지 않았을 가능성이 높기 때문에 중요한 문제점으로 삼는다.

overestimation과 optimism in the face of uncertainty
이 둘을 헷갈리지 말아야 한다고 하는데 후자의 경우는 $\epsilon$-greedy 방식과 같이 uncertainty에 기반한 exploration이 가져오는 긍정적인 영향과 구분지어 overestimation이 일으키는 것은 apparently certain한 상황에서(update 된 이후) learning에 impede 한 영향을 끼칠 수 있다. (이 부분은 좀 헷갈림)

DDQN
Double Q-Learning 과의 차이는


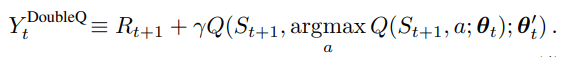
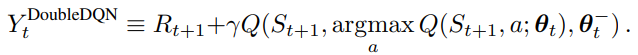
새로운 network를 만들어 내는 것이 아닌 target network와 origin network를 둬 origin network만 environment와 상호작용하고 N episode 마다 target network에 origin network를 복사하는 방향으로 soft update를 진행한다
이러한 방식은 새로운 Network와 그 parameter를 추가해 학습해야 하는 cost를 줄일 수 있고(Double Q-learning과 비교해) 원래 효과였던 overestimation 문제도 해결할 수 있다.
Target 함수 y를 제외한 나머지 알고리즘은 기존의 DQN을 최대한 따르고자 한다.