G2ANET

Intro

• agent 사이의 관계를 그래프로 매핑하여 GNN을 통과한 결과를 MARL 학습하는 방식 소개

• contribution

1. agent간 연결관계를 표현한 graph를 만들어내는 two-stage attention network 제시 - G2ANET
2. G2aNET에서 나온 결과를 기존 MARL 학습 방법과 결합해 나온 최종 결과 framework GA-Comm, GA-AC 제시

Background

• 논문에 등장하는 game abstraction이라는 말은 계산 complexity를 줄이기 위해 현재 상태를 smaller game으로 만드는 것이다.

• Attention 종류에는 두 가지가 있으며 우선 soft attention의 경우에는 모든 다른 대상에게 양수의 probability를 softmax로 부여한다는 특징이 있고 hard attention은 sampling 방식으로 관련이 있는 대상만 뽑아 계산을 진행한다는 특징이 있다.
  이러한 본질적인 특성으로 soft attetion은 gradient descent가 용이하지만 hard attention은 gradient 계산을 하기 위해 특별한 activation function을 적용해야 한다.

• 논문에서는 이 두 가지 attention을 혼합해 최종적인 관계를 얻어내는 것을 two-stage attention network 로 기술하고 있다.

G2ANET

• 이 network를 통해 나오는 output 각 노드는 agent를 의미하며 agent 사이의 edge는 그 둘 간의 연관성을 나타낸다. (undirected edge를 가짐)

• soft attention만 사용할 때의 단점
  모든 agent들에 대해 강제적으로 양수인 weight가 부여되므로 아무런 상관이 없는 agent와의 관계도 학습해야 한다는 단점이 있다. 이는 계산적인 측면에서 뿐만 아니라 진짜 연관성이 높은 agent가 줘야하는 영향도 감소시킨다는 단점도 존재한다.

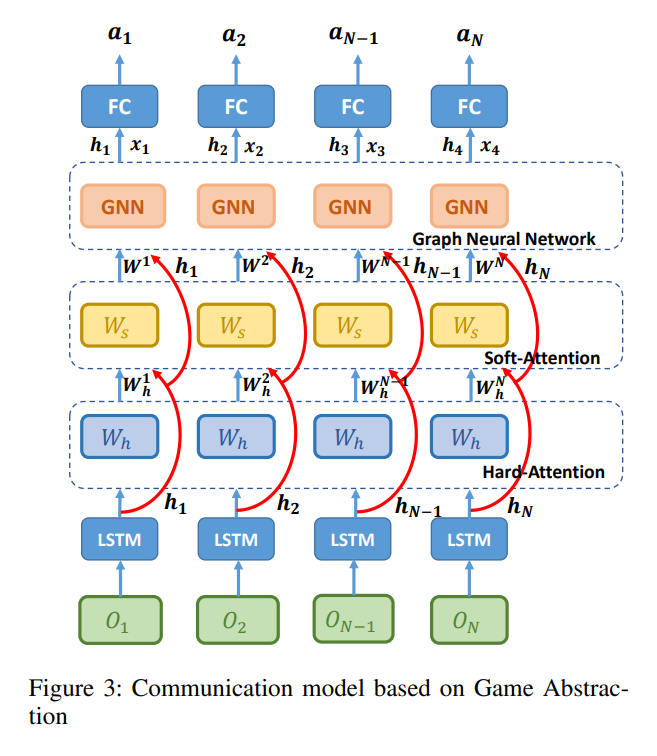
• 구조를 설명하기 전에 overall structure는 아래와 같다.
  
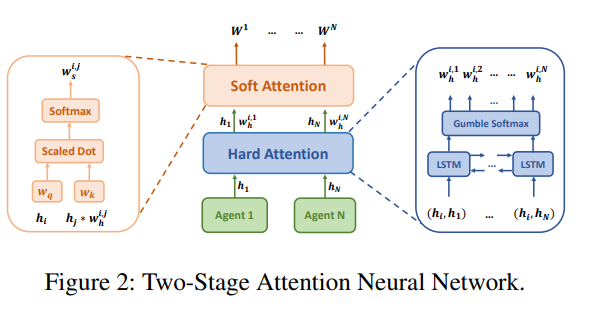
  먼저 agent들은 자신이 관찰한 $o_t$를 MLP에 전달하면 encoded feature vector $h_t$로 변환해준다. 이 벡터들은 먼저 hard attention 부분에 투입되어 agent간 연관성을 학습한다. (hard attention은 연관이 없는 경우 0, 연관성이 높을 경우 1을 부여한다.) 결과는 hard weight $W_h^{i,j}$로 나타나며 LSTM network를 사용한다. 각 timestep에서 두 agent 간의 연관성이 존재하는지 여부를 0,1 output으로 결정한다.

• hard attention에서 Bi-LSTM 모델을 사용하는 이유
  LSTM은 이전에 입력한 정보만을 output에 반영하기 때문에 MARL에서는 LSTM에 다른 agent 정보를 입력한 순서대로 결과에 영향을 받는 부작용을 만들기 때문에 나중 input도 반영할 수 있는 Bi-LSTM 모델을 채택하였다.
  이를 통해 나온 결과는 FC layer를 통과해 embedding 되어 아래와 같은 관계를 지닌 벡터로 출력된다.
  

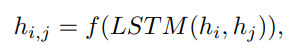
• 앞서 hard attention은 sampling 하기 때문에 backpropagation 이 어렵고 특수한 activation function을 사용한다고 했는데 여기서는 gumbel-softmax로 이를 대체한다. 위에서 설명한 embedded vector h는 이 activation을 통과한 후 hard attention의 weight가 되는데 식은 아래와 같다.
  

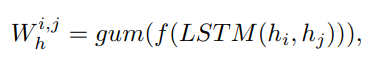
• 이 후 이 weight들은 key, query 값을 변환해주는 matrix와 곱해져 soft attention 연산을 수행한 최종적인 weight 값을 갖는다.
  
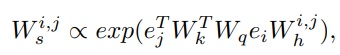
  e는 agent들의 feature vector들을 의미하며 첨자에 대응하는 W들은 embedded 된 벡터들을 다시 변환해주는 matrix라고 생각하면 된다.

• 이렇게 얻어진 weight는 GNN을 통과한 이후 다른 agent들이 자신에게 미치는 영향을 계산할 수 있게 된다.

Combined total framework

• GA-Comm 이라고 칭한 구조는 저자가 생각한 LSTM 아이디어에 REINFORCE policy 학습 방식을 결합한 것이다. REINFORCE가 어떤 방식이었는지 되돌아보면
  
  이 방법을 사용하려면 각 episode에서 action을 정하는 방식이 문제가 될 텐데 저자는 이를 아래와 같이 설명한다.
  먼저 각 timestep에 GNN의 output으로 등장하는 embedded vector $h_t$와 다른 agent들의 기여도를 의미하는 $x_t$는 아래와 같이 action을 정하는데 쓰일 수 있다.
  
  
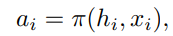
  여기서 $x_i$은 앞서 구한 hard, soft attention에 대한 weight들로 부터 계산할 수 있다. (애초 이 두 attention을 설계한 이유가 다른 agent가 미치는 영향을 실수로 나타내기 위함이었으므로)
  아래의 식은 각 attention model을 통과한 이후 나타나는 weight들을 의미하며 x에 대한 전체식은 action을 정하기 위해 마지막으로 필요한 항목을 충족시킨다.
  
  

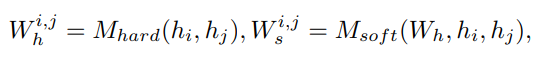
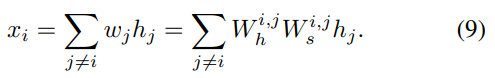
• 정리하자면 action을 구하기 위해 $h_i$, $x_i$가 필요한데 전자는 GNN을 통해 나오고 후자는 2 stage attention을 통과하면서 얻는 weight들을 통해 계산할 수 있다는 것이다.

• GA-AC
  앞서 읽은 MAAC 논문에 저자가 제시한 G2ANET을 적용한 약간의 변형을 가한 방식을 의미한다.
  앞서 MAAC에서 제시한 것과 같이 critic이 모든 agent의 action과 observation을 input으로 받는 것과 다른 agent들의 행동 종합 $x_i$를 weighted vector의 합으로 표현하는 방식까지 동일하다.
  
  
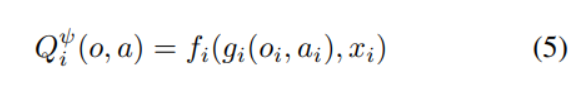
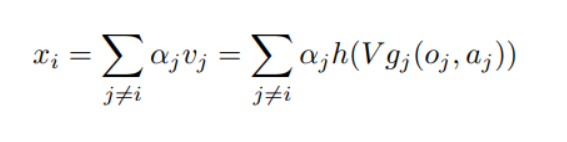
  weight $\alpha$를 계산하는 과정에서 two-stage attention이 사용된다는 점이 차이점인데 관찰결과와 ($o_i$) 선택한 행동 ($a_i$)에 대해 embedding 한 벡터값 ($e_i=g(o_i,a_i)$) 사이의 관계를 비교한 뒤 이 값은 LSTM을 통과시키고 (1 stage) 이 후 attention의 key-value matrix 변환 방식으로 값을 계산하여 최종적인 weight (논문에서는 $\alpha$ 를 $w_i$로 표현)를 산출