ROMA - MARL with emergent roles

Intro

• role based MARL 의 등장배경

1. 기존의 centralised Q or value function을 통해 모든 agent들이 policy를 학습하는 방식은 복잡한 task를 처리하는데 한계가 있다.
2. 그렇다고 모든 agent들에 각각의 policy network를 부여하는 것은 비슷한 action을 보이는 agent들에 대해서는 낭비를 발생시키는 꼴이다.

• 기존 role-based method 혼자 사용한 경우의 단점
  role을 나누기 위해 sub-task responsibility를 정하는 과정에서 domain knowledge가 필요하고 이는 dynamic 한 환경에 대해 scale up 되기 어렵다는 한계가 있음

• 그러므로 이 논문에서는 role-based method의 아이디어를 차용해 비슷한 role을 갖는 agent끼리는 비슷한 policy를 갖는 방향으로 학습을 진행시킨다.
  role과 policy 사이의 관계를 세우기 위해 ROMA 방식은 각 policy를 role에서부터 배우며 이 때 role은 (stochastic latent variable)로 표현되어 있다.

• 또한 두가지 regularizer를 소개하여 role과 policy 사이 관계를 표현할 수 있도록 한다.
  이 regularizer 들의 tractable variational estimation(? -아직 모르겠음)의 최적화가 role representation 의 좋은 결과를 이끌어냄을 보일 것이다.

Background

• 이전에 소개된 방식의 예시로는 VDN- value decomposition network 가 있으며 decentralized policy를 배우는 경우의 non-stationarity 문제를 극복하지만 이러한 CTDE(centralized training with decentralized execution) 방식은 complex task를 배우기에 적합하지 않은 경우가 있다. (diverse 한 responsibility와 skill을 필요로 하므로)

Method

• 반복적으로 설명하지만 ROMA는 비슷한 행동을 하는 agent간 shared learning이 가능하기 위해 role 개념을 도입한다.
  (여기서 shared learning은 training complexity를 줄이기 위한 목적임을 유추할 수 있다)
  

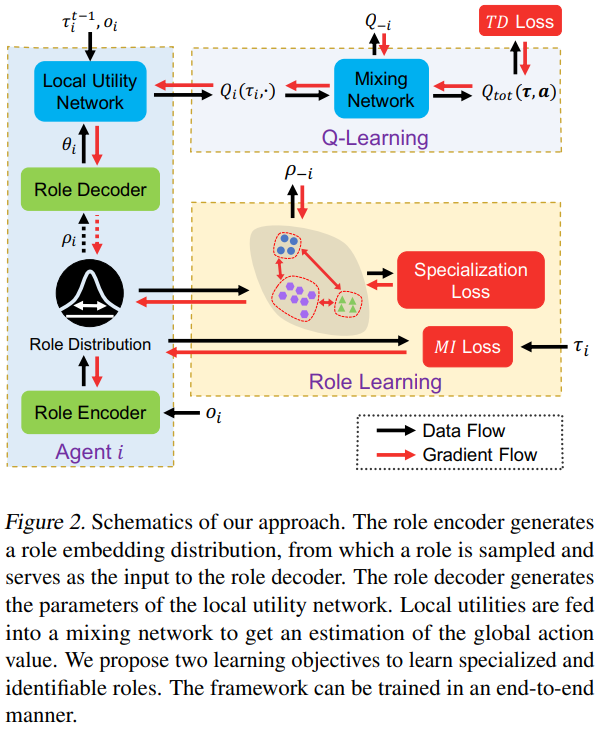
• 위의 그림과 같이 각 agent는 자신만의 local Q-function을 학습하며 이는 centralized training의 TD loss를 계산하기 위해 mixing network의 input 재료로 사용된다.
  CTDE(centralized training with decentralized execution) 방식을 차용했기 때문에 execution 순간에는 centralized mixing network는 제외되고 각 agent의 value function에 의해 local policy가 결정될 것이다.

• agent간 shared learning을 가능하게 하기 위해 ROMA는 아래와 같은 특성의 role를 학습할 것이다

  1. Dynamic : 환경이 dynamic 하게 바뀌어도 agent role은 그에 자동으로 adapt 할 수 있다.
  2. Identifiable : role은 각 agent의 behaviour 정보를 충분히 표현하고 있다.
  3. Specialized : 비슷한 role을 갖는 agent들은 비슷한 sub-task를 수행하게 될 것이다.

• 각 agent의 상황

1. 각 agent의 local utility function(혹은 indiviual policy) 는 parameter $\theta_i$에 기반하고 있고 이는 role $\rho_i$에 좌우된다. -> 위에 첨부된 figure 2. 의 role decoder 부분
2. 위의 role parameter $\rho_i$가 도출되는 방식은 아래와 같은 가우시안 분포로 부터이며 이 때 가우시안 분포의 parameter는 observation을 바탕으로 한 Neural Network로 계산된 latent space 에 놓인 변수들이다.
   
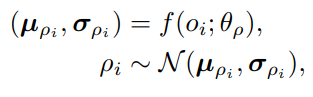
   latent space에 놓인 $\mu$와 $\sigma$를 도출하기 위해 사용된 network가 f임을 알 수 있다.
   또한 위에서 설명한 ROMA role의 특성 중 1번인 dynamic을 만족하기 위해서 f의 input으로 현재 agent의 partial observation $o_i$가 포함됨을 확인할 수 있다.
3. 이렇게 형성된 $\rho_i$가 agent의 indiviual policy $\theta_i$를 만드는 방법은 NN 인 g를 통과시키는 것이다.

   f <-> role encoder
   g <-> role decoder

• role의 두 번째, 세 번째 특징은 regularization 항을 통해서 이뤄지며 이 항 없이 목적함수 만을 추구할 경우 잘못된 방식의 학습이 이뤄질 수 있기 때문이다.

• dynamic 성질을 만족하기 위해 observation을 NN에 통과시켜 값을 얻었는데 이럴 경우 두 번째 성질인 behaviour 는 포함할 수 있지만 role이 너무 빠르게 바뀐다는 문제가 존재한다.
  이에 대항하여 role을 temporally stable하게 만들기 위해 long term behaviour를 반영하는 role을 추구하고 이를 만족하기 위해 $I(\tau_i;\rho_i|o_i)$ 를 최대화하는 방향으로 학습한다.

• I는 mutual information을 의미하는데 이는 서로 다른 두 stochastic varible 이 서로에 대해 얼마나 의존하는지를 나타내는 정도이며 수식으로는 아래와 같이 표현한다.
  $I(X;Y) = \sum_x\sum_x p(x,y)log(\frac{p(x,y)}{p(x)p(y)})$
  conditional mutual information의 경우 위의 식에 condition을 붙여도 되지만 아래와 같은 변형된 식으로도 똑같은 결과를 도출한다.
  $I(X;Y|Z) = E[log\frac{p(x|y,z)}{p(x|z)}]$

• mutual information 자체를 maximize 하거나 다루기에는 불편함이 존재하므로 I의 lower bound를 최대화하는 방향으로 loss function을 설정하게 되며 결론적으로 (I >= -x) 형태의 식을 얻게 되어 x를 loss function으로 설정하는 것이 바람직하다.

• 세 번째 조건인 비슷한 role를 갖도록 설정하는 방법은 behaviour 간 유사도를 어떻게 측정할 것인지 고민하는 것에서 시작된다

• 직관적으로 $I(\rho_i;\tau_j)$를 최대화하는 방법을 생각해 볼 수 있지만 어떤 agent 간 similar role를 가질 지 모르기 때문에 모든 조합에 대해 위의 값을 최대화 한다면 모든 agent들이 한 방향을 향해 같은 action을 취하는 잘못된 결과를 얻을 것이다. 이로부터 우리는 regularization 항이 필요함을 알 수 있으며 그 값은 dissimilarity model의 도입으로 해결할 수 있다.

• 이제 최대화 해야할 전체 식은 $I(\rho_i;\tau_j)+d_\phi(\tau_i,\tau_j)$이며 이 식은 두 agent 간 의존도 (I)가 낮은 경우 비슷하지 않은 정도 d가 증가하여 결국은 max function을 달성해야 한다는 식으로 이해할 수 있다.
  위의 조건과 동시에 $d_ij$를 원소로 갖는 matrix D의 non-zero element를 최소로 함을 목표로 한다. (두 agent 사이 관계를 최대로 파악하기 위하여)
  수식적으로는 아래와 같은 조건을 만족해야 하며 결국 D에 대한 frobenius norm을 최소화 하는 것이 목표이므로 loss function을 목표함수로 잡으면 될 것이다.
  
  
  
  

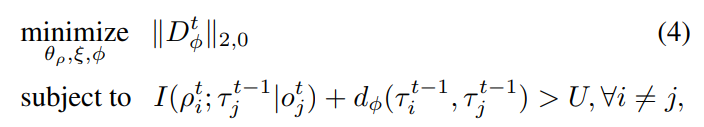
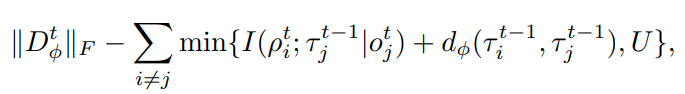
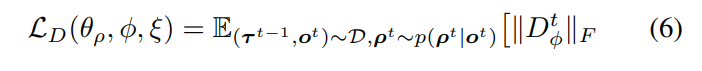
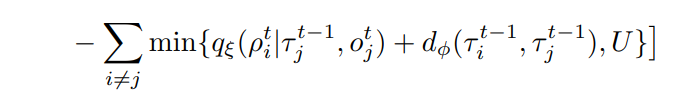
Overall architecture

• 전체적인 훈련 방식은 이전 소개된 논문인 QMIX를 기반으로 이뤄지며 원래 사용하던 $L_{TD}$ 와 더불어 regulation term을 고려한 추가적인 loss들(2,3 성질을 고려한)에 대응되는 상수 $\lambda$들을 곱해서 최종적인 loss function을 기준으로 파라미터 모음을 SGD 하면 될 것이다.
  
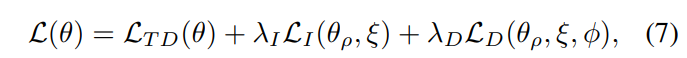
  원래 loss function은 아래와 같은 TD-error 였음을 기억하자
  

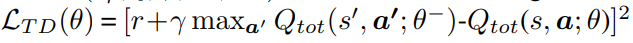
Conclusion

• Information에 관련된 식들은 직접 다루기가 어려워 expectation으로 lower bound를 고려하고 있는데 이를 변환하는 과정은 appendix를 참조하고 expectation의 기준이되는 확률 함수가 이해되지 않을 경우 직접 expectation 식을 전개해보면 밑을 이해할 수 있을 것이다.