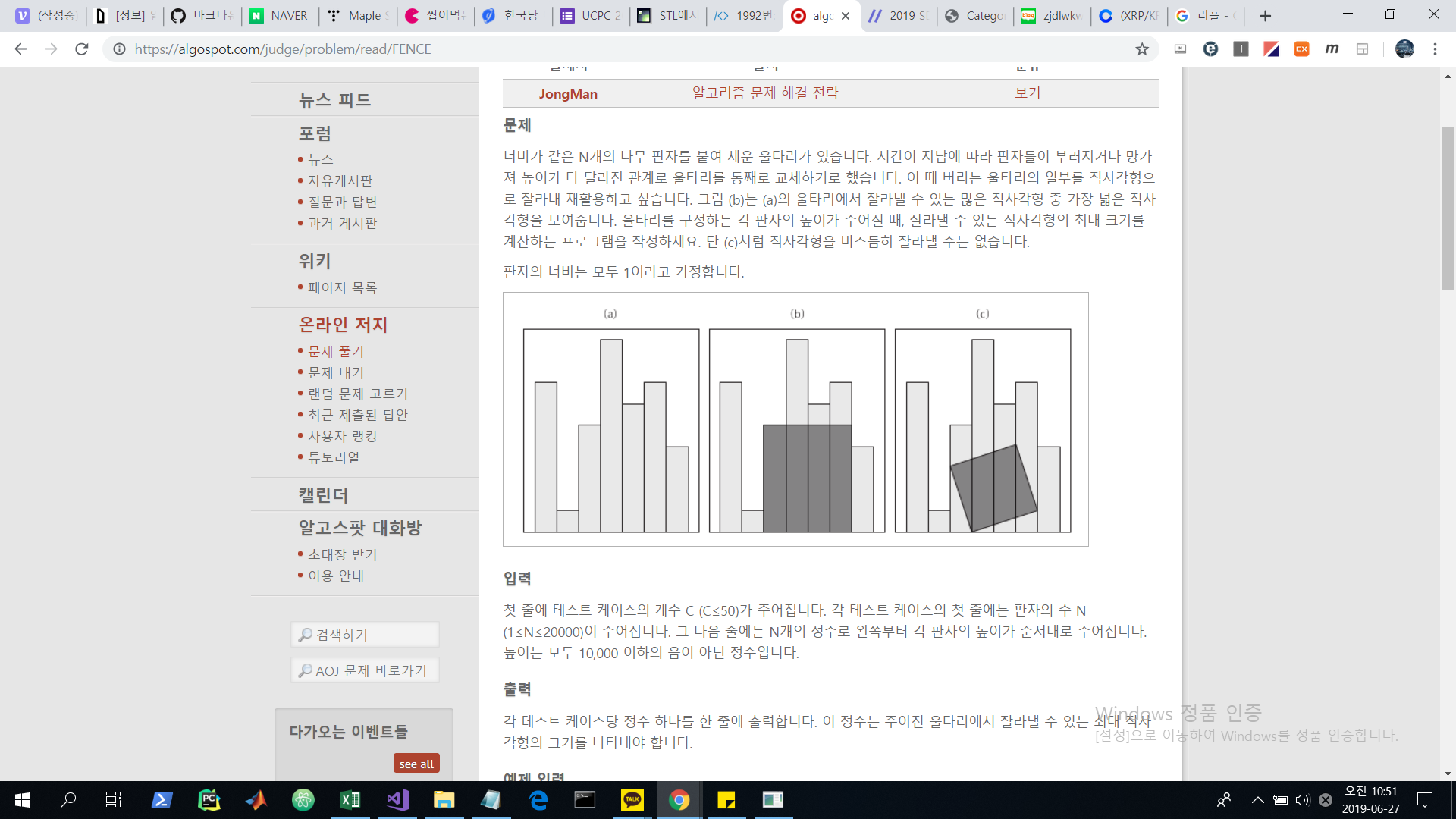
문제 파악
이 문제가 분할 정복을 통해 해결될 수 있는 문제라는 느낌은 바로 들었다. 내가 생각한 방식은 높이 1부터 한 칸씩 올라가면서 가장 낮은 높이를 가진 판자를 만나면 분할시키는 방식이었다. 시간복잡도는 바로 생각하지 못하고 우선 구현했는데, 구현 과정에서는 가장 낮은 높이를 가진 판자가 여러 개 들어있거나, 붙어있는 경우의 예외 처리를 해주는 과정에서 인덱스 설정에 어려움을 겪어 많은 시간이 걸렸고 결국 구현하지 못했다. 풀이를 보고 나서 알게된 시간 복잡도는 최악의 경우 O(n^2)으로 제한 조건을 위반할 가능성이 높은 방식이다. 또한 내가 생각한 방식은 한 칸씩 위로 올라가면서 최소 높이의 판자를 찾는 방식인데, 이렇게 할 필요 없이 그냥 매번 컨테이너의 원소 중 가장 작은 값을 가진 판자를 알 수 있어서 불필요한 과정을 포함했다고 볼 수 있다.
올바른 풀이
이 문제를 해결하는 알고리즘이 시간 제한을 통과하기 위해서는 n log n 이하의 시간복잡도를 가질 필요가 있다. 그러기 위해서는 분할 지점을 선택하는 과정에서 한 쪽으로 쏠린다거나, 분할 지점을 확인하기 위해 컨테이너의 모든 원소를 확인해서는 안된다. 이렇게 되면 최악의 경우 n^2의 시간 복잡도가 소요되는 것이 필연적이기 때문이다.
따라서 떠올리기 가장 쉬운 방법은 병합 정렬과 같이 매번 놓여있는 판자의 2분의1 지점을 분할 지점으로 선택하는 것이다.
책의 풀이는 이 방식을 이용해, 문제를 해결했는데 어떻게 아무 기준도 없이 2분의 1지점을 선택하는 것이 문제를 해결할 수 있는 지를 떠올리는 것이 가장 어려운 부분일 것이다.
먼저 절반을 기준으로 케이스를 총 세 가지로 나눈다. 첫 번째는 기준 왼쪽에 최대 사각형이 있는 경우, 두 번째는 오른쪽에 최대 사각형이 있는 경우, 세 번째는 사각형이 양쪽 모두에 겹쳐 있는 경우이다. 이 중 첫 번째와 두 번째 케이스는 재귀적으로 호출해 나가면서 해결할 수 있다. 세 번째 케이스는 어떻게 접근해야 하며, 얼마의 시간복잡도가 걸릴지 바로 쉽게 떠올리기 어렵다.
세 번째 케이스는 기준 양 쪽에 있는 두 판자를 이용해 너비를 확장해 나가면서 문제를 해결한다. 초기값은, 두 판자를 통해 얻을 수 있는 사각형의 최대 크기이다. 이사각형에서 오른쪽 또는 왼쪽으로 상자의 너비를 점차 확장해 나가면서 문제를 해결하는데, 방향을 결정하는 기준은 더 높은 높이의 판자가 있는 쪽이다. 확장을 마친 후 새롭게 얻게 된 사각형에서 재귀적으로 사각형의 크기를 점차 확장해 나간다. 더 높은 크기의 판자 방향으로 확장하는 것이 결국 최대 크기의 사각형을 구하는 데 올바른 기준이 될 수 있는 것은, 어차피 높은 쪽으로 확장하더라도 반대 방향(더 낮은 높이의 판자)이 최대 사각형에 포함될 경우 재귀적으로 확장해 나가는 과정에서 아까 선택되지 않은 방향이 반드시 포함되기 때문에 결과적으로 항상 최대 크기의 사각형이 선택되게 된다.
결국 문제 해결 과정을 단순하게 설명하자면 다음과 같다.
1. 주어진 너비의 절반을 기준점으로 삼는다.
2. 기준점의 오른쪽과 왼쪽에 걸치는 사각형의 최대 크기를 계산한다.
3. 기준점의 왼쪽과 오른쪽에 대해 위 과정을 재귀 호출한다.
4. 각 방식의 값을 비교해 최대값을 반환한다.
느낀점
난이도가 높은 문제는 단순히 분할 정복을 통한 해결법을 생각해낸다고 풀 수 있는 것이 아니라, 효율적으로 분할하는 방식을 생각해내야 문제의 시간 제한을 통과할 수 있다. 효율적인 분할 방법은 분할이 균등하게 이루어 지는 것이다. 분할이 균등하게 이루어지지 않는 경우가 있으면, 최악의 경우 시간복잡도가 매우 크게 증가할 수 있기 때문이다.
이는 퀵 정렬과 병합 정렬의 비교에서도 유사하게 나타나는데, 병합 정렬은 매번 균등하게 분할하기 때문에, 시간 복잡도가 항상 일정하다. 그러나 퀵 정렬은 평균적으로는 병합 정렬의 시간복잡도와 같지만, 최악의 경우 시간 복잡도가 n^2이 되어 상대적으로 비효율적인 정렬 방법이 되버린다.
