[알고리즘] 그리디 알고리즘 (Greedy)

이 글은 혼자 공부하면서 적어간 내용이기에 평어체로 작성되었고 틀린 내용이 있을 수 있습니다.
이 점 양해부탁드리며 틀린 내용 지적, 질문은 언제든 환영합니다!

그리디 알고리즘 (Greedy Algorithm)

Greedy(탐욕스러운, 욕심 많은)
탐욕 알고리즘이라고도 불리는 그리디 알고리즘은 현재의 상황에서 봤을 때 가장 최적의 답만을 골라 최종 해답에 도달하는 방법이다.

• 현재의 상황에서 봤을 때라는 구문에서 알 수 있듯이 그 당시에는 최적의 답이었지만 최종적으로는 그 답이 최적이었다는 보장이 되지 않는다.
• 따라서 그리디 알고리즘을 적용하는 문제는 지역적으로 최적이면서 전역적으로도 최적인 문제들이다.
  👉 그리디를 적용할 수 있는 문제인지 분석이 중요하다.

그리디를 사용할 수 있는 문제?

• 다음 두 가지 조건을 충족하면 그리디를 사용할 수 있다.

1. 앞에서의 선택이 다른 값에 영향을 주지 않아야 한다. (탐욕적 선택 속성)
2. 각 상황에서 최적인 해가 모든 경우에서 최적의 해여야 한다. (최적 부분 구조)

그리디를 사용했을 때와 최적해가 다른 경우

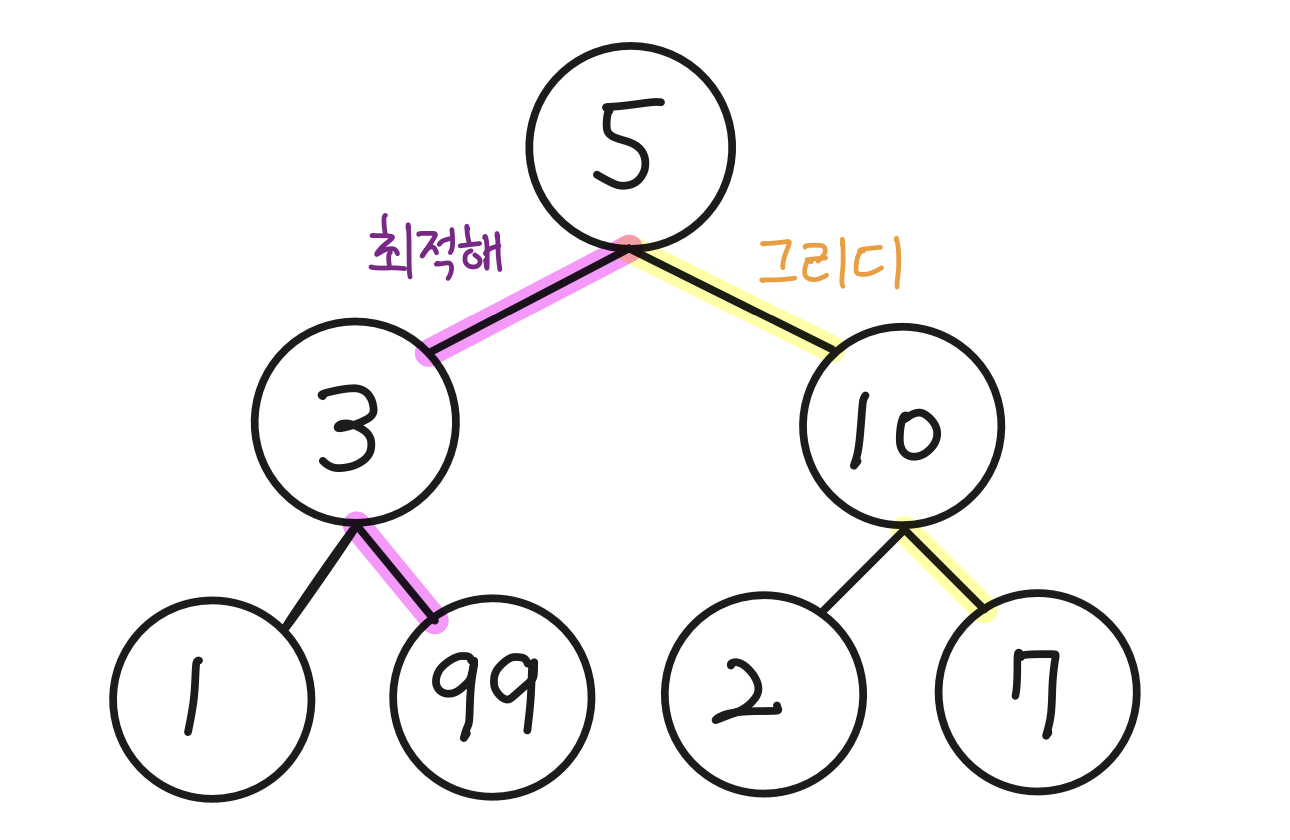
• 위와 같이 세 수를 골라 합을 구한다고 했을 때, 두번째 수를 선택하는 상황에서 더 큰 값인 10이 최적 해로 판단되어 10을 선택하지만 최종적인 최적 해는 5-3-99를 선택했을 때이다.
• 이처럼 아무 문제에나 그리디를 사용하지 않도록 조심해야 한다.

예시

문제

백준 5585번 문제는 지불해야 하는 돈(1000미만의 정수)을 하나 입력받고 받을 잔돈의 개수를 출력하는 문제이다.

생각

1엔짜리 5개는 5엔, 5엔짜리 2개는 10엔으로 대체 가능하므로 액수가 가장 큰 잔돈부터 거슬러주면 최소 개수를 구할 수 있을 것이다.
👉 각 상황의 최적의 해는 주어진 잔돈 중에서 가장 큰 잔돈을 주는 것이다.

풀이

#include<iostream>

using namespace std;

int main()
{
    int n, ans=0, change[6]={500, 100, 50, 10, 5, 1};
    cin >> n;
    n=1000-n;
    for(int i=0; i<6; i++) {
        ans += n/change[i]; // 잔돈의 개수
        n %= change[i]; // 거슬러준만큼 빼줌
    }
    cout << ans;
}

• 그 때 상황에 맞는 가장 최적의 해, 즉 가장 큰 단위의 잔돈을 거슬러주고 남은 돈을 다음으로 큰 단위의 돈으로 거슬러주는 과정을 반복하면 최종적인 최적의 해가 구해져있다.
• 거스름돈이 720엔일때, 720/500=1개 -> 220/100=2개 -> 20/10=2개
  => 5개가 가장 적은 거스름돈의 개수이다.

참고문헌

https://hanamon.kr/알고리즘-탐욕알고리즘-greedy-algorithm/
https://velog.io/@kyunghwan1207/그리디-알고리즘Greedy-Algorithm-탐욕법