이 글은 혼자 공부하면서 적어간 내용이기에 평어체로 작성되었고 틀린 내용이 있을 수 있습니다.
이 점 양해부탁드리며 틀린 내용 지적, 질문은 언제든 환영합니다!시간복잡도란?
문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 가리킨다.
즉, 특정한 크기의 입력에 대해 프로그램의 실행 시간 (알고리즘의 수행 시간)을 계산해볼 수 있는 것이다.
표기법
- Big-0 (빅-오) : 최악의 경우
- Big-Ω (빅-오메가) : 최선의 경우
- Big-θ (빅-세타) : 둘의 평균
3가지 표기법이 있으며 각각 최악, 최선, 둘의 평균을 고려하여 시간을 구해보는 방법이다.
알고리즘 문제 풀이(Problem Solving, 이하 PS)를 하는데 있어서는 사실상 Big-O(빅-오) 표기법만 알면 된다.
왜 Big-O 표기법을 알아야 하는가?
PS에서 가장 중요한 것은 문제를 풀 수 있다는 것 그 자체겠지만 알고리즘을 구현하는데 있어 얼마나 빠르게 실행되는지, 얼마나 효율적으로 메모리를 사용하는지 또한 중요하다.
알고리즘 문제들에는 항상 시간 제한이 주어지고 이 주어진 시간 안에서 실행을 마쳐야 한다.
100개의 입력을 넣어본다 했을 때, 99개는 시간 안에 통과한다해도 단 1개의 입력에서 시간 안에 출력이 나오지 못한다면 시간 초과가 되는 것이다.
👉 그렇기에 최악의 상황을 고려하는 Big-O 표기법을 꼭 알고 있어야 한다.
예시
이해하기 쉽게 실제 문제를 보면서 정리해보자.

백준 온라인 저지 1463번 문제를 가져와보았는데 시간 제한 항목을 보면 실행 시간이 0.15초를 넘기면 '시간 초과'로 실패로 처리된다.
1. 조건
- 컴퓨터는 초당 약 1억번의 연산이 가능하다.
-> 이 가정은 알고리즘 문제 풀이 시 항상 기억할 것! - 입력 : 1<=N<=10^6 인 정수 N이 주어진다.
2. 생각
- 0.15초 안에 실행을 끝내려면 최대 연산 횟수를 15,000,000번을 넘기면 안되겠구나.
(단순 계산일뿐, 입출력 시간 등을 고려했을 때 실제론 더 적다.) - 언제 가장 연산하는데 오래 걸릴까?
- N이 1, 2, 3일 때 보다 클 때 당연히 더 오래 걸리지 않을까?
- 그럼 입력 최댓값 N=1,000,000일 때를 주목해보자.
- N이 1, 2, 3일 때 보다 클 때 당연히 더 오래 걸리지 않을까?
3. 풀이
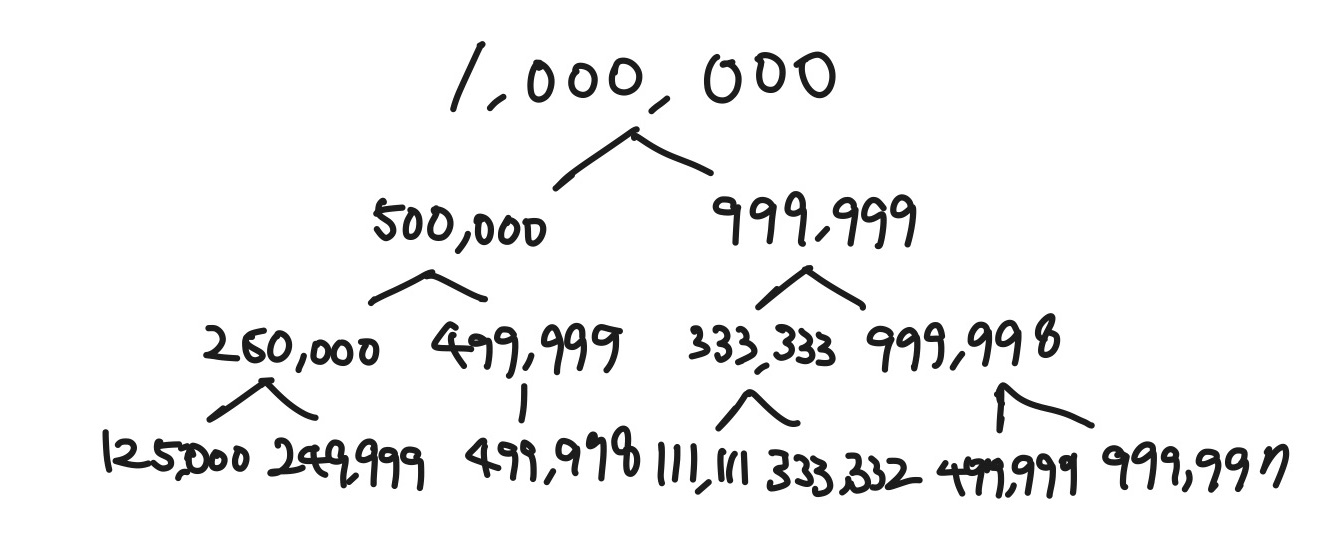
- 이와 같은 방식으로 1이 나올 때까지 계속 진행하여 가장 먼저 나온 1이 몇 번 걸렸는지 출력한다? 무언가 잘못된 것 같다.
2로 나누어 떨어지는 수 일 때, 3으로 나누어 떨어질 수 없으므로 하나의 수에서 최대 2번 이어나갈 수 있다. 이는 최대 2^N번의 연산을 거친다는 것인데
최대 2^N번의 연산=최악의 경우를 뜻하는 것이므로Big-O 표기법으로 나타낼 수 있고 이는 O(2^N)으로 표시한다.
👉 2^24 ≒ 16,000,000 인데 N=10^6 대입 시 2^(1,000,000)이므로 O(2^N)의 시간복잡도를 가진 알고리즘은 써서는 안된다는 것을 알 수 있다!
그래서, 이 문제에는 O(N)의 시간복잡도를 가지는 DP (Dynamic Programming) 알고리즘을 사용하여 풀어야만 한다.
이제 Big-O 표기법이 어떤 식으로, 왜 쓰이는지 알게 되었고 조금만 더 알아보자.
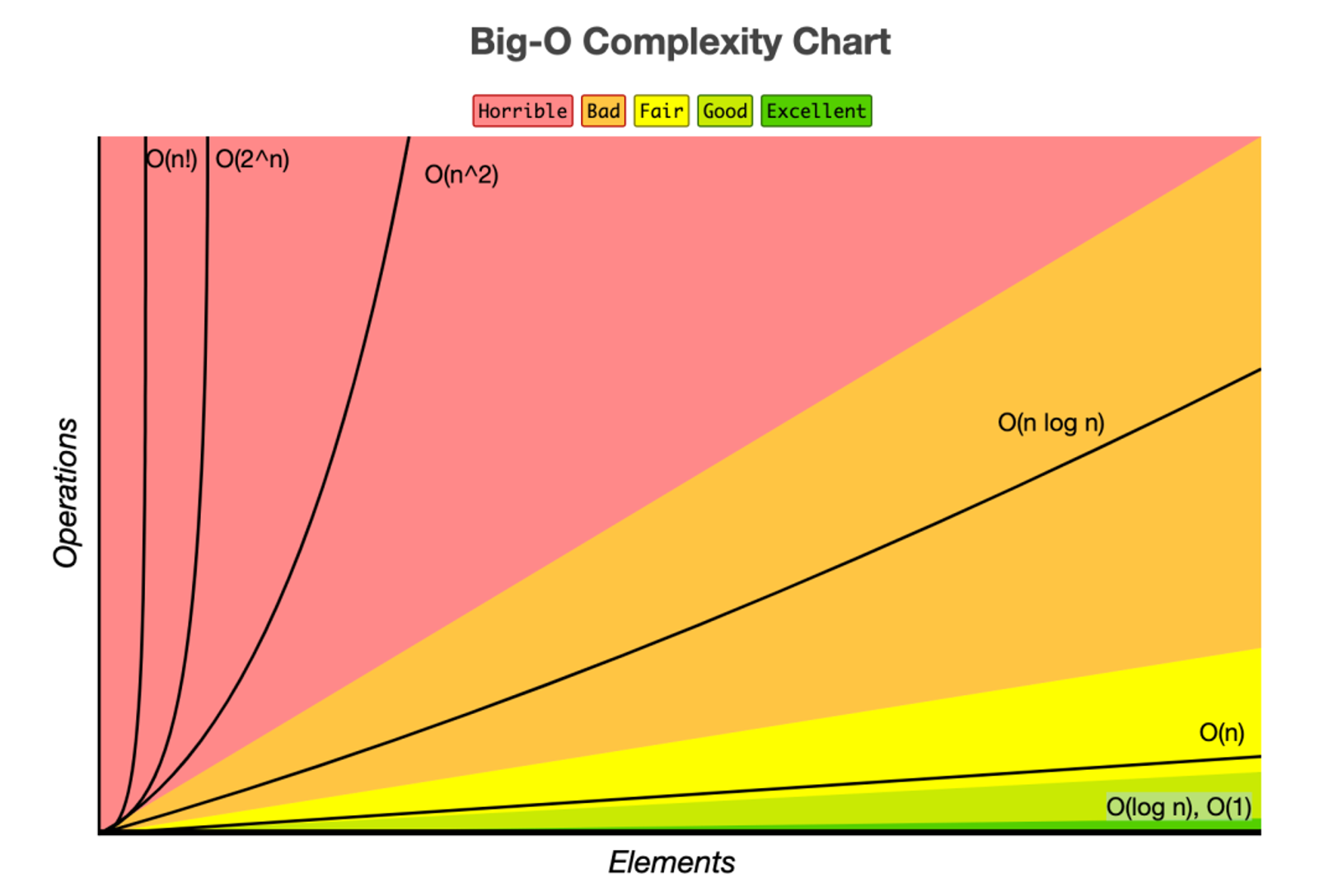
O(1)
constant complexity라고 하여, 입력값이 증가하더라도 시간이 늘어나지 않는다.
int arr[N]={1,2,3, ...};
cout << num[1] << endl;O(log n)
Logarithmic complexity라 하며 빅-오 표기법 중 O(1) 다음으로 빠른 시간 복잡도를 가진다.
대표적으로, 이분 탐색 (binary search) 알고리즘이 여기 해당한다.
O(n)
Linear complexity라 하며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.
for(int i=0; i<n; i++) {
cout << arr[i] << endl;
}O(n^2)
quadratic complexity라 하며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다.
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
cout << arr[i][j] << endl;
}
}O(2^n)
Exponential complexit라고 부르며 지수 함수는 기하급수적으로 커지기 때문에 매우 느린 시간 복잡도를 가진다.
앞서 본 예시가 이에 해당하고 거의 모든 상황에서 쓰지 않는 것이 좋다.
