1. 신장 트리(Spanning Tree)
: 그래프 내의 모든 정점을 포함하는 트리
신장 트리의 특징
- DFS, BFS를 사용하여 그래프에서 신장 트리를 찾을 수 있다.
- 탐색 도중에 사용된 간선만 모으면 됨.
- 하나의 그래프에는 많은 신장 트리가 존재할 수 있다.
- 모든 정점이 연결되어 있어야 하고, 사이클을 포함해서는 안된다.
=> n개의 정점을 정확히 n - 1개의 간선으로 연결
2. 최소 신장 트리(Minimum Spanning Tree = MST)
: 신장 트리 중 사용된 간선들의 가중치 합이 최소인 트리
최소 신장 트리의 특징
- 간선의 가중치를 고려하여 최소 비용의 신장 트리를 선택한다.
- 즉, 간선의 가중치 합이 최소여야 한다.
- 신장 트리의 특징과 같은 특징을 공유한다.
3. MST 구현 방법
: 아래 두 알고리즘은 모두 그리디 알고리즘의 일종이다.
1) 크루스칼(Kruskal) 알고리즘
- 간선 중심 알고리즘
- 모든 간선을 가중치 기준으로 오름차순 정렬하고, 이 간선들을 순서대로 모든 정점이 연결될 때까지 연결하는 알고리즘
- Union-Find 알고리즘을 이용해 구현 가능
- 상수 시간 복잡도 O(1)을 가지기 때문에 간선 정렬 방법이 전체 시간 복잡도를 좌우.
- 퀵 정렬로 간선 가중치를 정렬하면 퀵 정렬의 시간 복잡도인 O(ElogE)이 시간복잡도가 됨.
(E : 간선 개수)
- 퀵 정렬로 간선 가중치를 정렬하면 퀵 정렬의 시간 복잡도인 O(ElogE)이 시간복잡도가 됨.
1-1) 크루스칼 알고리즘 동작 방식
- 그래프의 간선들을 가중치 기준 오름차순으로 정렬한다.
- 정렬된 간선 리스트들을 순서대로 선택하여 간선의 정점들을 연결한다.
2.1. 이 때 정점을 연결하는 것은 Union-Find의 Union으로 구현한다. - 만약 간선의 두 정점 a, b가 이미 연결되어 있다면 연결하지 않고 넘어간다.
- 위의 과정을 반복해 최소 비용의 간선들만 이용해 모든 정점이 연결된다.
1-2) 구현 예시
- 아래의 그래프에서 크루스칼 알고리즘을 사용하여 MST 구하기
(출처 : https://m.blog.naver.com/ndb796/221230994142)
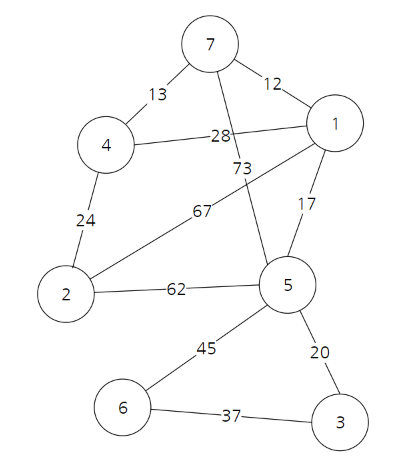
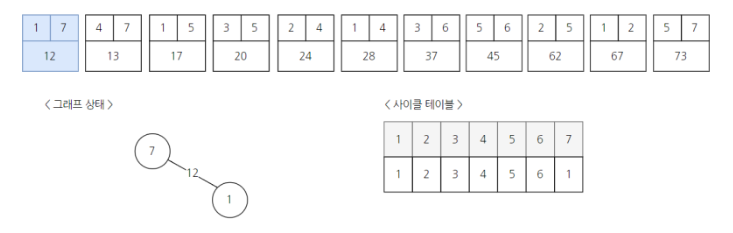
1) 간선들을 가중치 오름차순으로 정렬한다.

2) 가장 가중치가 낮은 간선의 정점들부터 연결(Union)하기 시작한다.
여기서는 1과 7을 연결하고 부모를 합쳐 7의 부모가 1로 변경된다.
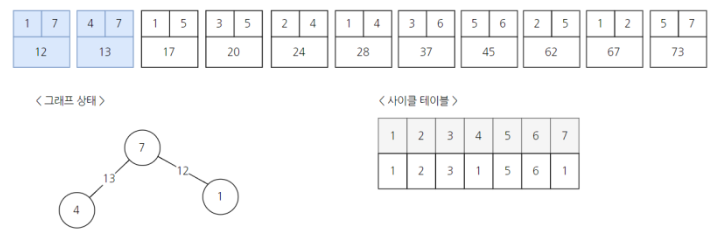
3) 4와 7을 연결하고 부모를 합쳐 4의 부모가 1로 변경된다.
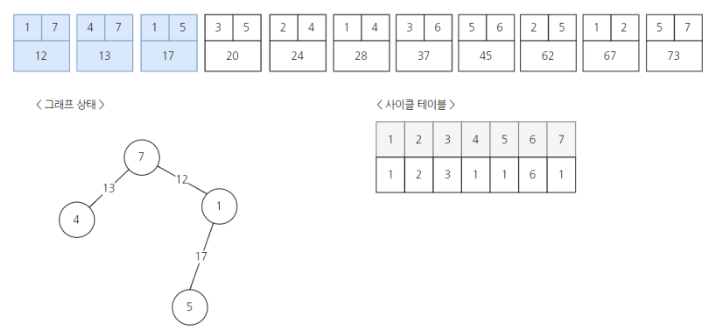
4) 1과 5를 연결하고 부모를 합쳐 5의 부모가 1로 변경된다.
5) 3과 5를 연결하고 부모를 합쳐 3의 부모가 1로 변경된다.
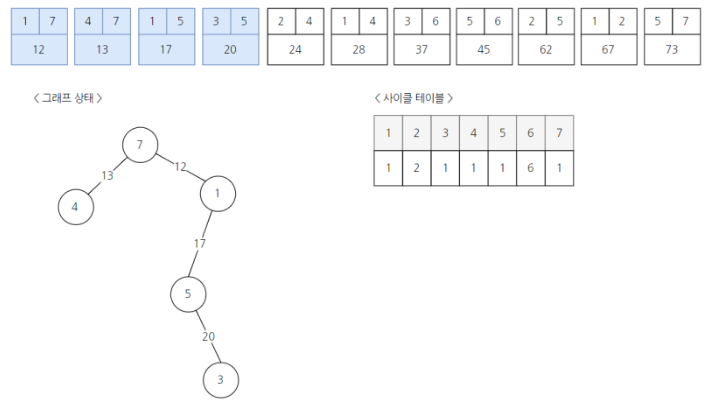
6) 2와 4를 연결하고 부모를 합쳐 2의 부모가 1로 변경된다.
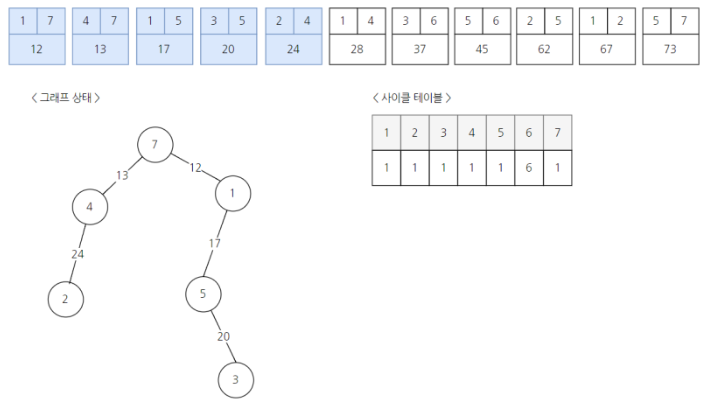
7) 1과 4의 부모는 이미 같기 때문에 간선 연결 없이 생략한다.
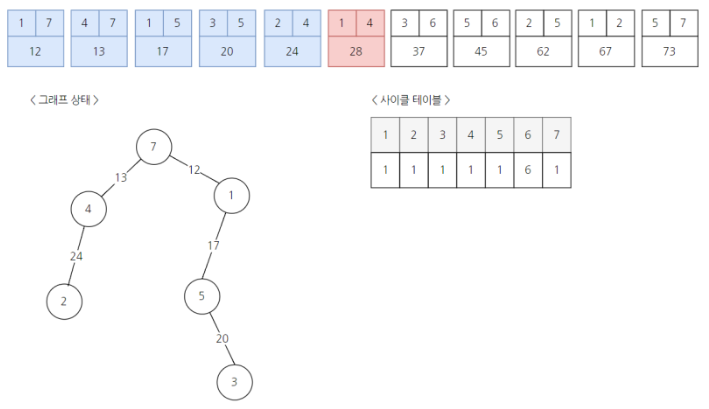
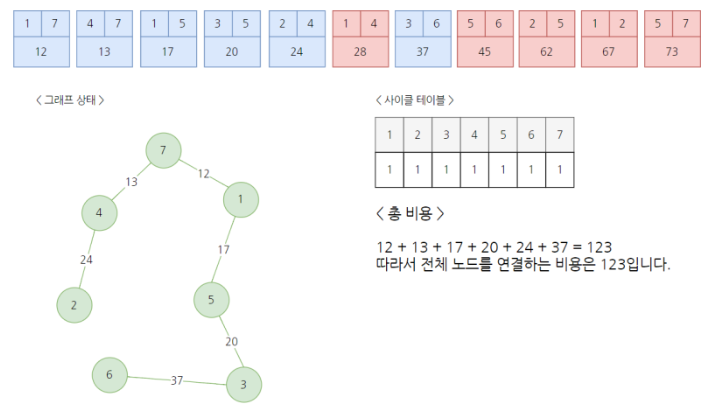
8) 이러한 방식으로 반복하여 모든 노드가 연결되었을 때 MST가 완성되고, 모든 노드를 연결할 때 드는 최소 비용을 알 수 있다.
🖥️ 1-3) 코드 구현
#include <iostream>
#include <vector>
#include <algorithm>
#include <tuple>
using namespace std;
int parent[8];
typedef tuple<int, int, int> tiii;
// n 노드에 연결된 부모 노드 반환
int getParent(int n)
{
if (parent[n] == n) return n;
return parent[n] = getParent(parent[n]); // 연결되어 있는 부모 노드 반환과
} // 동시에 연결되어 있는 노드의 부모 노드를 갱신
// a와 b의 부모를 비교해 더 작은 쪽으로 부모를 합침.
void unionParent(int a, int b)
{
a = getParent(a);
b = getParent(b);
if (a < b)
parent[b] = a;
else
parent[a] = b;
}
// a와 b의 부모가 같은지 (== 두 노드가 같은 그래프에 있는지 == 연결된다면 사이클이 있는지) 확인
bool findParent(int a, int b)
{
a = getParent(a);
b = getParent(b);
return (a == b);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(); cout.tie();
// 가중치 합
int sum = 0;
// 각 노드의 부모를 자기 자신으로 초기화
for (int i = 0; i < 7; i++)
parent[i] = i;
vector<tiii> edges; // 각 간선 정보를 저장. tuple에는 간선을 연결하는 (가중치 / 정점 a / 정점 b) 저장
// 각 간선 정보 입력
edges.push_back(tiii(12, 7, 1));
edges.push_back(tiii(13, 7, 4));
edges.push_back(tiii(17, 5, 1));
edges.push_back(tiii(20, 5, 3));
edges.push_back(tiii(24, 4, 2));
edges.push_back(tiii(28, 4, 1));
edges.push_back(tiii(37, 6, 3));
edges.push_back(tiii(45, 6, 5));
edges.push_back(tiii(62, 5, 2));
edges.push_back(tiii(67, 2, 1));
edges.push_back(tiii(73, 7, 5));
// 가중치 기준 오름차순 정렬 (tuple은 첫 번째 원소 값 기준으로 정렬됨)
sort(edges.begin(), edges.end());
// 각 간선 확인하면서 노드들 연결
for (int i = 0; i < edges.size(); i++)
{
int curA = get<1>(edges[i]);
int curB = get<2>(edges[i]);
// 간선에 연결된 두 노드의 부모가 같지 않으면 (같은 그래프에 있지 않으면)
if (!findParent(curA, curB))
{
unionParent(curA, curB); // 부모 결합
sum += get<0>(edges[i]); // 가중치 총 합 누적
}
}
cout << "최소 신장트리 가중치 합 : " << sum << endl;
}
[실행 결과]
최소 신장트리 가중치 합 : 1232) 프림(Prim) 알고리즘
- 정점 중심 알고리즘
- 임의의 시작점에서 현재까지 연결된 정점들로부터, 연결되지 않은 정점들에 대해 가장 가중치가 작은 정점을 연결하는 알고리즘
- 트리 집합을 단계적으로 확장하는 것이 핵심
- Priority Queue를 이용한 최소 힙으로 구현 가능
- 간선들을 최소 힙에 추가하는 것은 최대 E번, 최소 힙에 최대 V개의 정점들이 들어오기 때문에 추가된 정점의 가중치를 최소 힙 내부에서 정렬하는 것은 최대 logV만큼 수행.
- 따라서 모든 간선 (E) * 간선을 통해 삽입된 정점의 가중치 정렬 (logV) = O(ElogV)
(E : 간선 개수 / V : 정점 개수)
- 따라서 모든 간선 (E) * 간선을 통해 삽입된 정점의 가중치 정렬 (logV) = O(ElogV)
2-1) 프림 알고리즘 동작 방식
- 임의의 정점을 시작점으로 선택해 최소 신장 트리에 추가. 해당 정점과 연결된 모든 간선을 우선순위 큐에 추가
- 우선순위 큐에서 비용이 가장 작은 간선을 선택
- 해당 간선이 최소 신장 트리에 포함된 두 정점을 연결하는지 아닌지 확인
3.1. 만약 두 정점이 모두 최소 신장 트리에 있을 경우 연결하지 않고 넘어감.
3.2. 만약 정점 u는 최소 신장 트리에 포함되어있고, 다른 정점 v는 아닐 경우 해당 간선과 정점 v를 최소 신장 트리에 추가 후, 정점 v와 최소 신장 트리에 포함되지 않는 정점을 연결하는 모든 간선을 우선순위 큐에 추가 - 최소 신장 트리에 (정점 개수 - 1)개의 간선이 추가될 때까지 2, 3번 과정을 반복한다.
2-2) 구현 예시
- 아래의 그래프에 프림 알고리즘을 사용해 MST 구하기
(출처 : https://blog.encrypted.gg/1024)
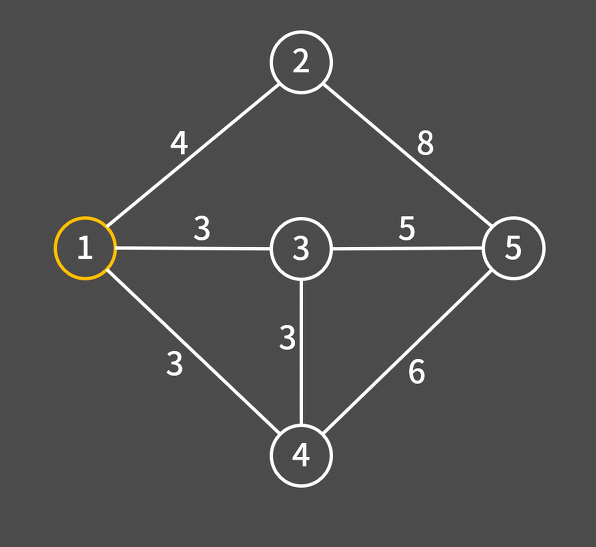
1) 임의의 정점 1에서 시작해 이와 연결된 간선 1-2, 1-3, 1-4를 우선순위 큐에 삽입한다.
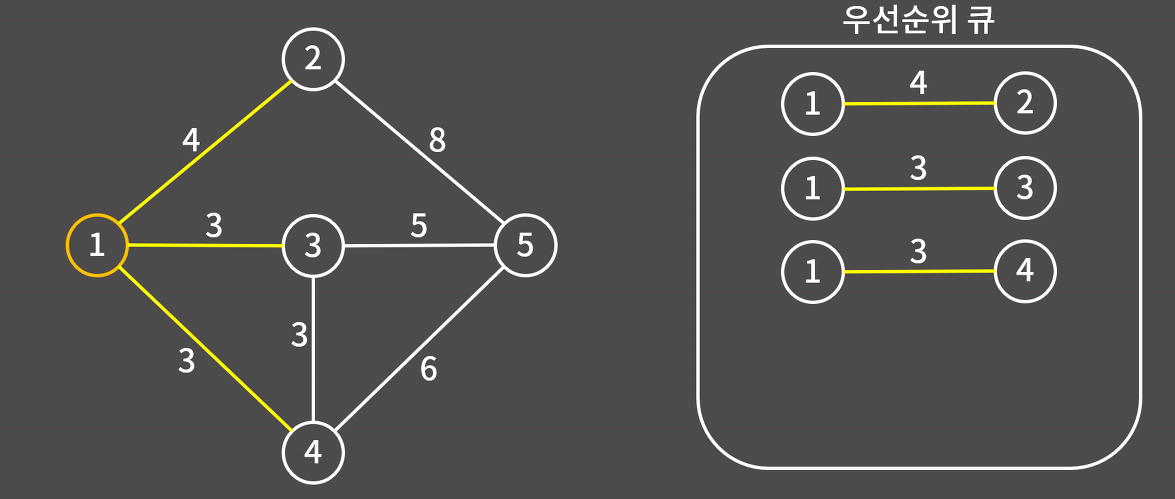
2) 우선순위 큐에 있는 간선 중 가장 가중치가 작은 1-3을 우선순위 큐에서 제거하고 1과 3을 연결한다.
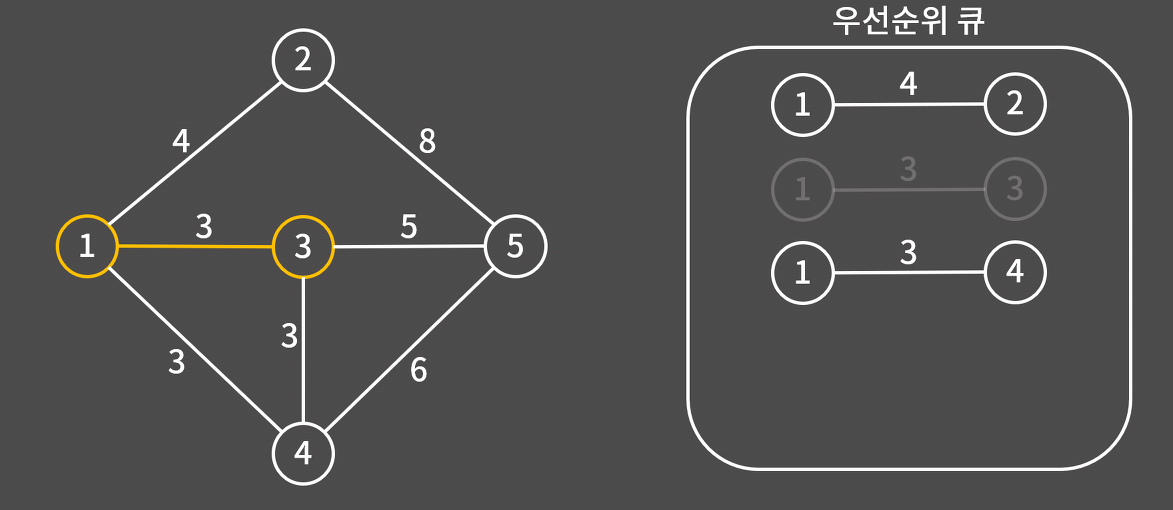
3) 3과 연결된 간선 3-4와 3-5를 우선순위 큐에 삽입한다. 3-1은 양 노드가 모두 최소 신장 트리에 포함되어있으므로 넘어간다.
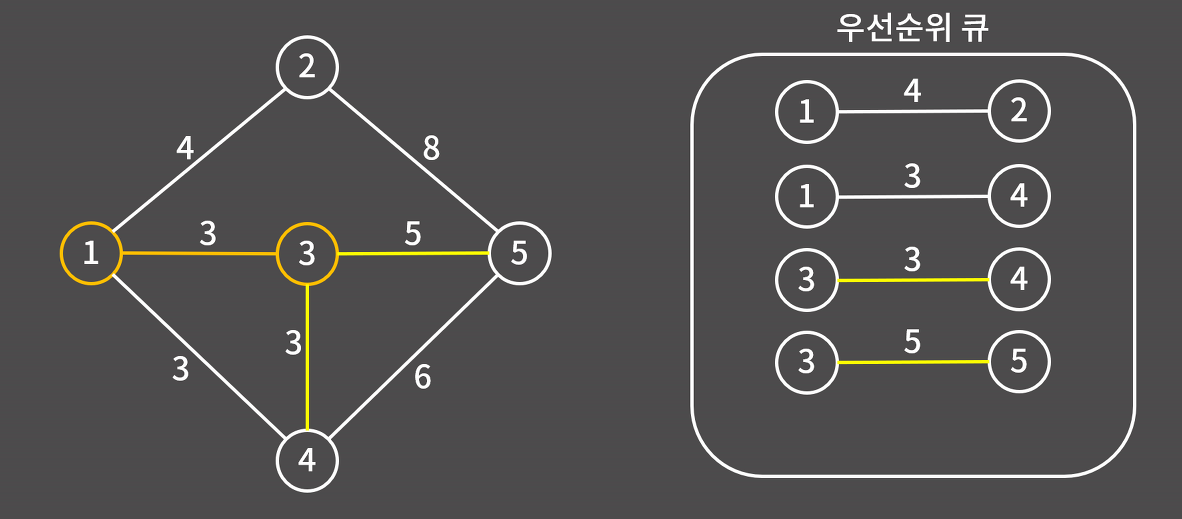
4) 우선순위 큐에 있는 간선 중 가장 가중치가 작은 3-4를 우선순위 큐에서 제거하고 3과 4를 연결한다.
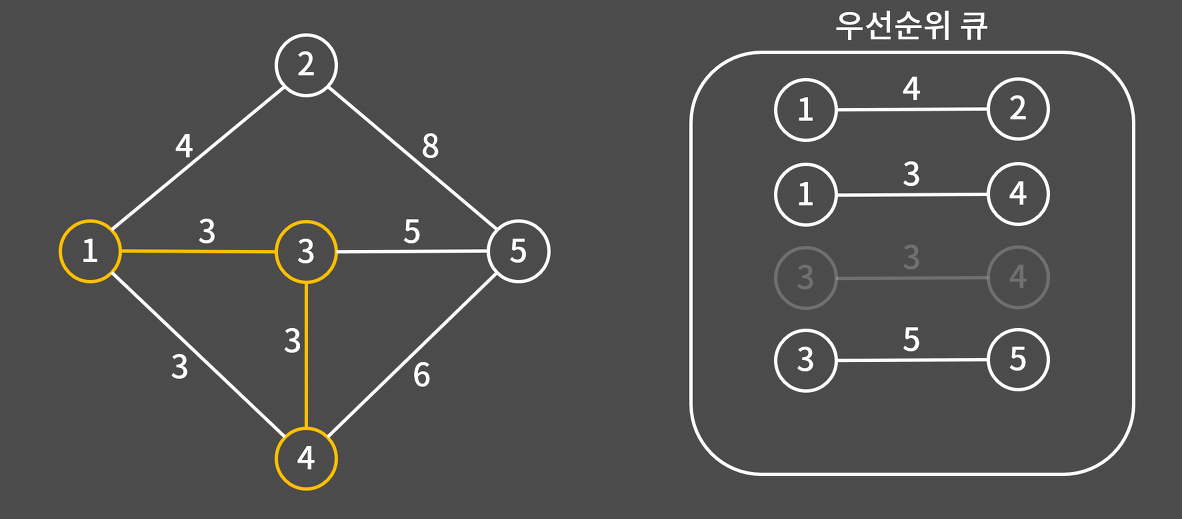
5) 4와 연결된 간선 4-5를 우선순위 큐에 삽입한다. 4-1과 4-3은 양 노드가 모두 최소 신장 트리에 포함되어있으므로 넘어간다.
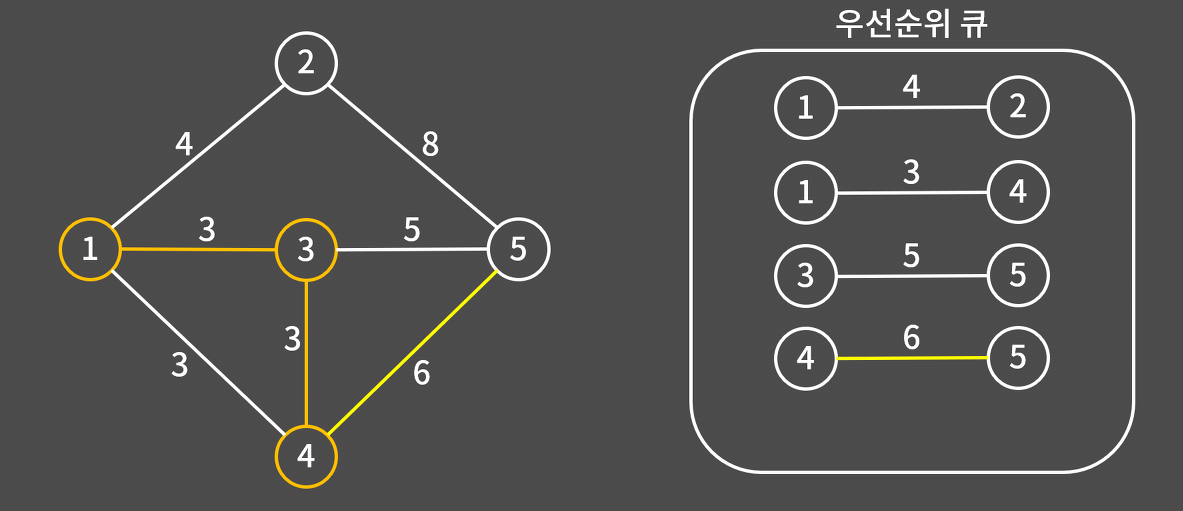
6) 우선순위 큐에 있는 간선 중 가장 가중치가 작은 1-4를 우선순위 큐에서 제거한다. 1과 4는 이미 최소 신장 트리에 있으므로 넘어간다.
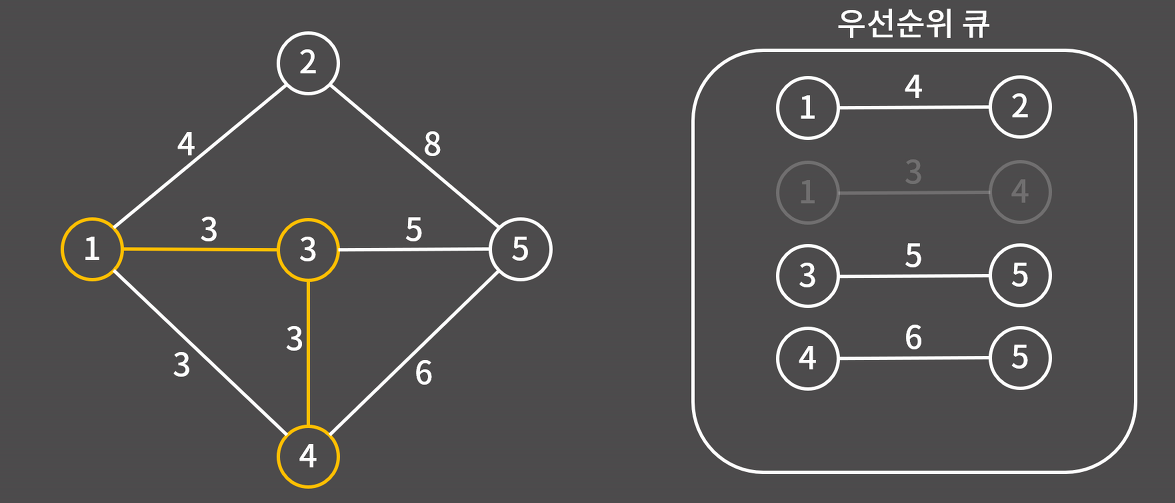
7) 우선순위 큐에 있는 간선 중 가장 가중치가 작은 1-2를 우선순위 큐에서 제거하고 1과 2를 연결한다.
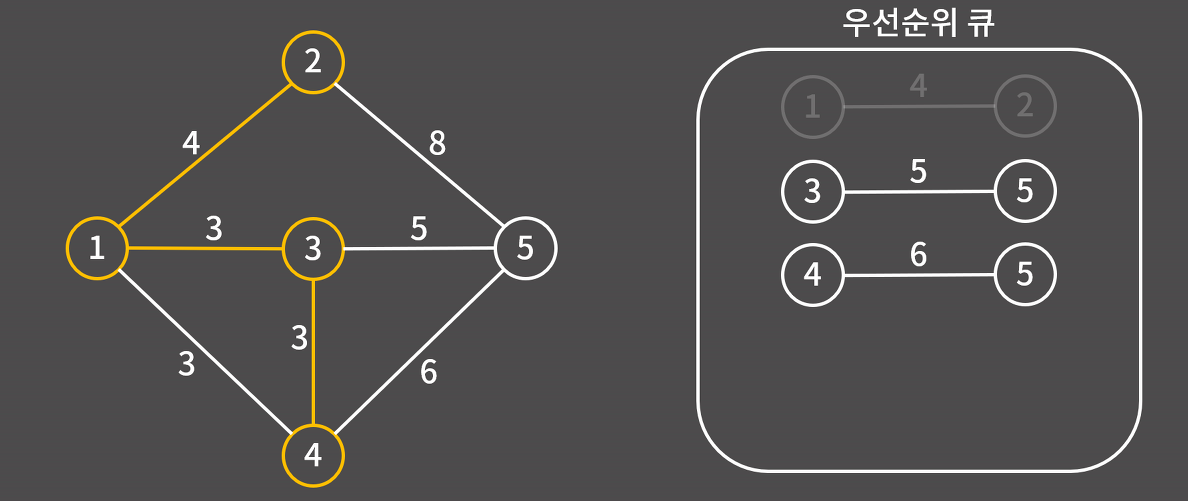
8) 2와 연결된 간선 2-5를 우선순위 큐에 삽입한다. 2-1은 양 노드가 모두 최소 신장 트리에 포함되어있으므로 넘어간다.
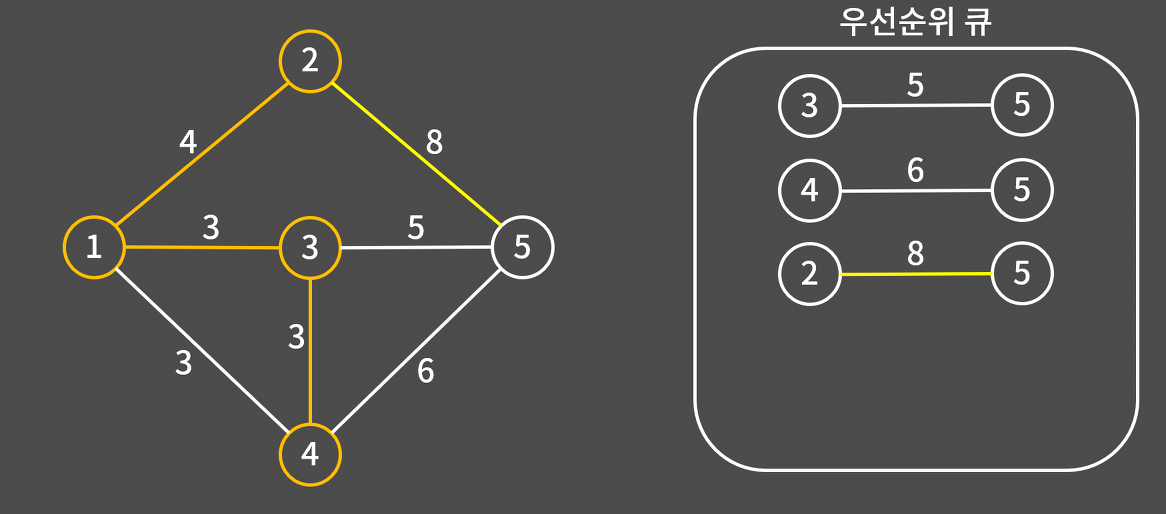
9) 우선순위 큐에 있는 간선 중 가장 가중치가 작은 3-5를 우선순위 큐에서 제거하고 3과 5를 연결한다.
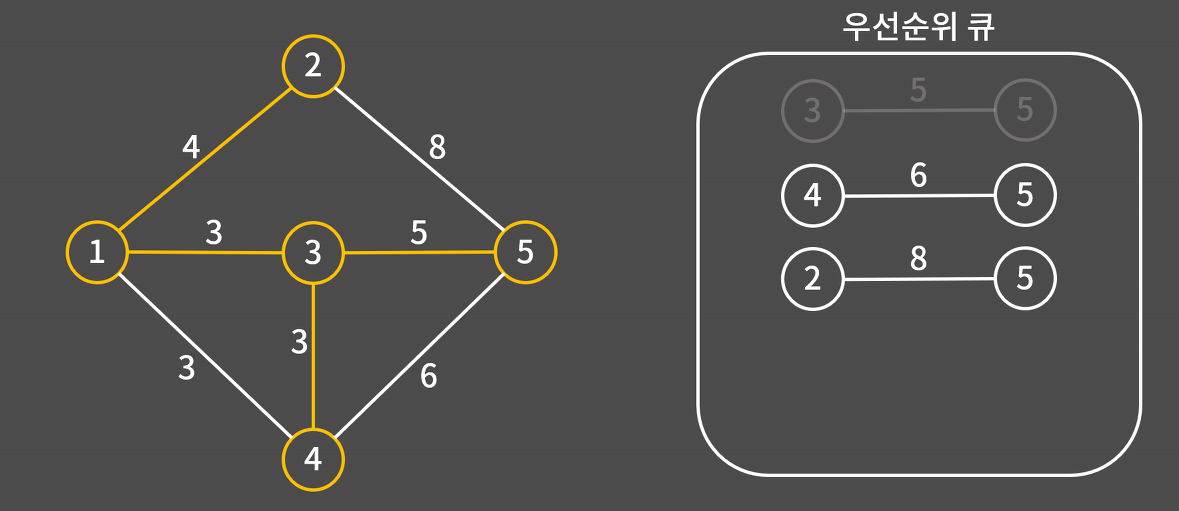
10) 총 간선이 4개가 되어 모든 정점을 연결시켰으므로 최소 신장 트리가 완성된다.
🖥️ 2-3) 코드 구현
#include <iostream>
#include <vector>
#include <algorithm>
#include <tuple>
#include <queue>
using namespace std;
typedef pair<int, int> pii; // (가중치, 이어지는 정점)
vector<vector<pii>> edges(6); // 각 정점에 연결된 간선들에 대한 정보들의 벡터를 저장하는 벡터
bool mst[6];
int answer = 0;
void prim()
{
priority_queue<pii, vector<pii>, greater<pii>> pq; // 간선 저장하는 우선순위 큐 선언
int i = 1, count = 1; // i : 가장 마지막에 추가된 노드의 번호, count : 최소 신장 트리에 추가된 노드 개수
while (true)
{
mst[i] = true; // 최소 신장 트리에 i 노드 추가
// i 노드와 연결된 간선 전부 탐색해 상대 노드가 아직 최소 신장 트리에 없는 경우 우선순위 큐에 해당 간선 추가
for (int j = 0; j < edges[i].size(); j++)
{
int curNode = edges[i][j].second;
if (!mst[curNode])
pq.push(edges[i][j]);
}
// 우선순위 큐 가장 앞에 있는 간선 하나 꺼내서 상대 노드가 아직 최소 신장 트리에 추가되지 않은 노드라면, 최소 신장 트리에 추가 및 가중치 합과 count 누적
// 이미 최소 신장 트리에 있는 노드라면 생략하고, 최소 신장 트리에 없는 노드가 나올 때까지 우선순위 큐 탐색
for (int k = 0; k < pq.size(); k++)
{
pii curEdge = pq.top();
pq.pop();
if (!mst[curEdge.second])
{
i = curEdge.second;
answer += curEdge.first;
count++;
break;
}
}
// 모든 노드가 최소 신장 트리에 추가 된다면 탐색 종료
if (count == 5)
return;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(); cout.tie();
edges[1].push_back(pii(4, 2));
edges[1].push_back(pii(3, 3));
edges[1].push_back(pii(3, 4));
edges[2].push_back(pii(4, 1));
edges[2].push_back(pii(8, 5));
edges[3].push_back(pii(3, 1));
edges[3].push_back(pii(3, 4));
edges[3].push_back(pii(5, 5));
edges[4].push_back(pii(3, 1));
edges[4].push_back(pii(3, 3));
edges[4].push_back(pii(6, 5));
edges[5].push_back(pii(8, 2));
edges[5].push_back(pii(5, 3));
edges[5].push_back(pii(6, 4));
prim();
cout << "최소 신장트리 가중치 합 : " << sum << endl;
}
[실행 결과]
최소 신장트리 가중치 합 : 153) 크루스칼 알고리즘과 프림 알고리즘 선택 기준
- 간선 개수 = E, 정점 개수 = V 라고 할 때
- 크루스칼 알고리즘의 시간 복잡도 : O(ElogE)
- 프림 알고리즘의 시간 복잡도 : O(ElogV)
따라서 간선이 많을 때는 프림 알고리즘 / 정점이 많을 때는 크루스칼 알고리즘이 유리하다.
👁️🗨️ 참고
https://m.blog.naver.com/ndb796/221230994142
https://www.youtube.com/watch?v=LQ3JHknGy8c
https://ongveloper.tistory.com/376
https://www.weeklyps.com/entry/%ED%94%84%EB%A6%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Prims-algorithm
https://www.youtube.com/watch?v=4wA3bncb64E
https://blog.encrypted.gg/1024
