1. 트리의 지름이란?
: 가장 먼 두 정점 사이의 거리 혹은 가장 먼 두 정점을 연결하는 경로를 의미한다.
2. 트리의 지름을 찾는 알고리즘
: DFS 또는 BFS를 사용하여 찾을 수 있다.
1) 임의의 정점 x로부터 가장 멀리 있는 정점인 u를 DFS(BFS)로 구한다.
2) 구해진 u를 시작 정점으로 하여 가장 멀리 있는 정점인 v를 DFS(BFS)로 구한다.
3) 이렇게 구해진 정점 u와 정점v 사이의 거리가 트리의 지름이다.
✔️ DFS와 BFS로 어떤 정점에서 가장 멀리 있는 정점을 구할 수 있는 이유
: DFS와 BFS는 완전탐색 알고리즘이기 때문에 모든 정점을 방문하게 된다. 때문에 임의 정점에서 출발하여 각 정점에 도착할 때까지 이동한 거리를 알 수 있고, 이 거리가 가장 먼 정점이 해당 정점에서 가장 먼 정점이 될 것이다.
✔️ 예시 트리
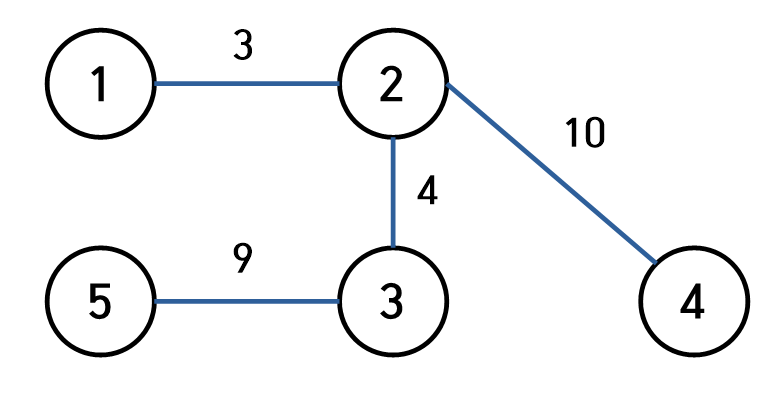
- 시작 정점을 임의로 1이라고 할 때
- 1에서 가장 멀리 있는 정점은 5 (거리 : 16)
- 5에서 가장 멀리 있는 정점은 4 (거리 : 23)
- 따라서 트리의 지름은 23이다.
- 시작 정점을 임의로 3이라고 할 때
- 3에서 가장 멀리 있는 정점은 4 (거리 : 14)
- 4에서 가장 멀리 있는 정점은 5 (거리 : 23)
- 따라서 트리의 지름은 23이다.
➡️ 이와 같이 어떤 정점에서 시작해도 같은 결과가 나오게 된다.
3. 트리의 지름 알고리즘 증명
- 두 개의 노드
u,v를 사용해 트리의 지름이d(u, v)라고 가정한다.- 트리의 특징으로 인해
u에서v로 가는 경로는 오직 하나만 존재한다.
- 트리의 특징으로 인해
- 임의의 정점
x에서 시작해 DFS(BFS) 알고리즘을 사용해 가장 먼 정점을 얻는다고 할 때- 만약
x가u라면 항상v노드를 얻고,v에서 DFS(BFS) 실행 시u를 얻는다.
- 만약
-
이처럼 임의의 정점
x에서 가장 거리가 먼 정점이u또는v라면 (지름 안에 있는 정점이라면), 그 점에서 가장 거리가 먼 점까지의 경로가 트리의 지름이라는 것은 자명하다. -
따라서 "임의의 정점
x에서 가장 거리가 먼 정점이 지름 안에 있는 정점이 아니다." 라는 명제가 모순이라는 것을 보이면 해당 알고리즘을 증명할 수 있다.
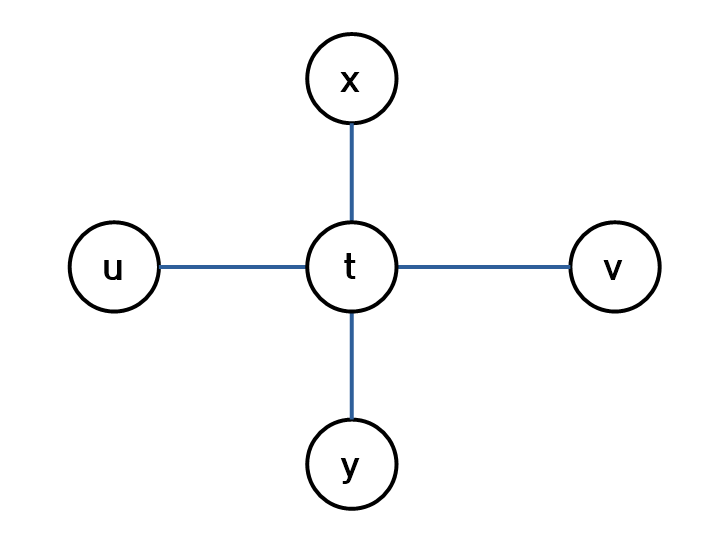
1) 임의의 정점 x가 u가 아니고, 그 점에서 가장 먼 정점이 u, v가 아닌 다른 정점 y라고 가정한다. (임의의 정점에서 가장 거리가 먼 정점이 지름 안에 있는 정점이 아님을 가정한 것)
또한 경로(u, v)와 (x, y)는 정점 t에서 만난다.
2) 정점 x에서부터 가장 먼 정점은 y이기 때문에
d(x, y) > d(x, u), d(x, v)
경로 (x, t)는 위 세 경로가 모두 공유하는 경로라 같은 거리이므로 이를 제외하면
d(y, t) > d(u, t), d(v, t)
3) 정점 u에서부터 v까지의 거리 : d(u, v) = d(u, t) + d(v, t)
정점 y에서부터 v까지의 거리 : d(y, v) = d(y, t) + d(v, t)
- 원래대로라면
d(u, v)는 트리의 지름이기 때문에 가장 길어야 한다.- 그런데 위에서
d(y, t) > d(u, t)라는 결과가 나왔고,d(v, t)는 두 경로가 공유하는 경로이기 때문에 이를 제외하면 d(u, v)가 d(y, v)보다 짧다는 결론이 나온다. 이 경우에는d(u, v)가 트리의 지름이라는 처음의 가정과 모순된다.
- 그런데 위에서
4) 따라서 d(u, v)가 실제 트리의 지름이기 위해서는 임의의 정점 x로부터 가장 먼 정점은 u 또는 v가 되어야 한다. (== 지름 안에 있는 정점이어야 한다.)
5) 이를 통해 "임의의 정점 x에서 가장 거리가 먼 정점이 지름 안에 있는 정점이 아니다." 라는 명제가 모순임을 밝혔기 때문에 해당 알고리즘은 트리의 노드를 구해준다는 것이 증명된다.
👁️🗨️ 출처
https://blogshine.tistory.com/111
https://blog.myungwoo.kr/112
📌 개인 학습을 위해 인터넷 자료를 찾아 작성한 글이므로 정확한 내용이 아닐 수 있습니다.
