Chap 02. 재귀 (Recursion) [윤성우의 열혈 자료구조]

*본 내용은 [윤성우의 열혈 자료구조] 책과 강의를 보고 공부하면서 요점 정리한 내용입니다.

Chap 02-1: 함수의 재귀적 호출의 이해

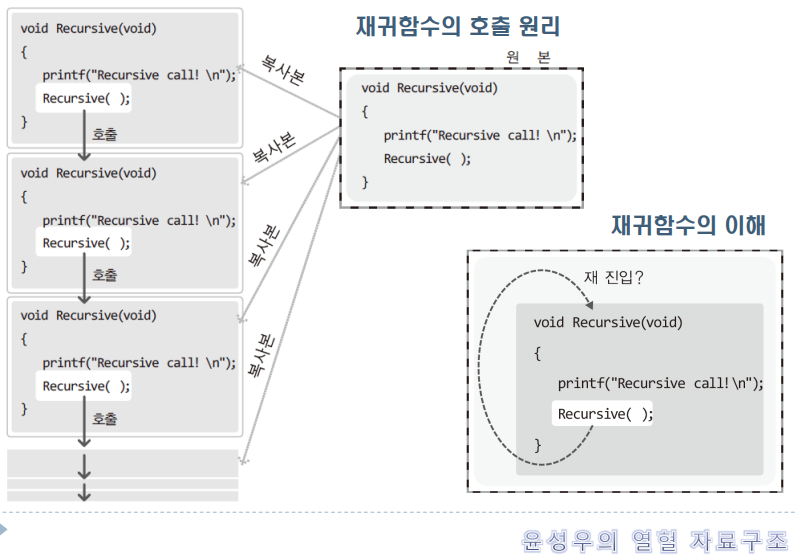
🔳 재귀함수의 기본적인 이해

• 재귀는 재 진입의 개념이 아닌, 명령문의 복사본이 만들어져서 그 복사본이 실행된다고 생각하자.
• 재귀함수는 탈출조건이 필요하다.

#include<stdio.h>
void Recursive(int num)
{
	if (num <= 0)	//재귀의 탈출조건
		return;		//재귀의 탈출
	printf("Recursive call! %d \n", num);
	Recursive(num - 1);
}

int main() 
{
	Recursive(3);
	return 0;
}

실행결과

Recursive call! 3
Recursive call! 2
Recursive call! 1

🔳 팩토리얼의 재귀적 구현

#include<stdio.h>
int Factorial(int n) 
{
    if (n == 0)
        return 1;
    else
        return n * Factorial(n - 1);
}

int main() 
{ 
    printf("1! = %d \n", Factorial(1));
    printf("2! = %d \n", Factorial(2));
    printf("3! = %d \n", Factorial(3));
    printf("4! = %d \n", Factorial(4));
    printf("9! = %d \n", Factorial(9));

    return 0; 
}

실행결과

1! = 1
2! = 2
3! = 6
4! = 24
9! = 362880

※ 재귀 공부할 때 주의할 점

• 함수의 [호출 관계 + 호출 순서]를 파악하는 것은 재귀함수를 공부할 때 꼭 필요한 것은 아니다.
  재귀관계가 꼭 필요한 문제일수록 호출 관계, 호출 순서를 파악하는게 어려울 뿐만 아니라 이해에도 큰 도움이 되지 않는다. 특히 호출 순서를 파악하는 것이 어려운데 재귀를 공부하면서 호출 관계와 호출 순서를 파악하는 것에 집착하지 않는게 좋다.

• 재귀적 문제 해결 방법

1. 문제 확인
2. 재귀적 해결책
3. 코드 작성
4. test --> 확인되면 OK!
   (호출 관계, 호출 순서에 집착 No!)

Chap 02-2: 재귀의 활용

🔳 피보나치 수열

• 피보나치 수열
  첫 번째 항의 값이 0이고 두 번째 항의 값이 1일 때, 이후의 항들은 이전의 두 항을 더한 값으로 이루어지는 수열을 말한다.

  0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ...

• 피보나치 수열의 구성

  수열의 n번째 값 = 수열의 n-1번째 값 + 수열의 n-2번째 값

• 피보나치 수열의 표현
  

• 코드의 구현
  
  

• 예제

#include<stdio.h>
int Fibo(int n) 
{
	if (n == 1)
		return 0;
	else if (n == 2)
		return 1;
	else
		return Fibo(n - 1) + Fibo(n - 2);
}

int main() 
{
	int i;
	for (i = 1; i < 15; i++)
		printf("%d ", Fibo(i));

	return 0;
}

실행 결과

0 1 1 2 3 5 8 13 21 34 55 89 144 233

🔳 이진 탐색 알고리즘

• 이진 탐색의 알고리즘의 핵심

1. 탐색 범위의 중앙에 목표 값이 저장되었는지 확인
2. 저장되지 않았다면 탐색 범위를 반으로 줄여서 다시 탐색 시작

• 예제

int BSearchRecur(int ar[], int first, int last, int target)
{
	int mid;
	if (first > last)	//탈출조건: first와 last가 역전되면 탈출
		return -1;		//-1의 반환은 탐색의 실패를 의미

	mid = (first + last) / 2;	//탐색의 대상에서 중심에 해당하는 인덱스 값 계산

	if (ar[mid] == target)	//타겟이 맞는지 확인
		return mid;
	else if (target < ar[mid])
		return BSearchRecur(ar, first, mid - 1, target);	//앞부분을 대상으로 재 탐색
	else
		return BSearchRecur(ar, mid + 1, last, target);		//뒷부분을 대상으로 재 탐색
}

Chap 02-3: 하노이 타워

🔳 하노이 타워

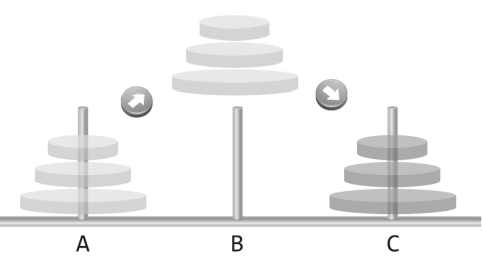
• 하노이 타워
  원반을 A에서 C로 이동하기. 옮기는 과정에서 B를 활용한다.
  

• 제약사항

1. 원반은 한 번에 하나씩만 옮길 수 있다.
2. 옮기는 과정에서 작은 원반 위에 큰 원반이 올려져서는 안된다.

• 하노이 타워의 반복패턴 연구
  '원반 4개를 A에서 C로 이동해야하는 문제'를 '원반 3개를 옮기는 문제'로 축소할 수 있고,
  이를 일반화 시키면 다음과 같다.

(원반 3개를 하나의 원반덩이로 생각하면 편하다.)

하노이 타워	반복패턴	일반화
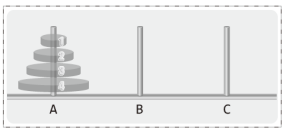	목표. 원반 4개를 A에서 C로 이동	목표. 큰 원반 n개를 A에서 C로 이동
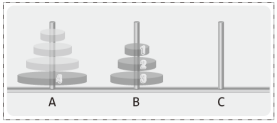	1. 작은 원반 3개를 A에서 B로 이동	1. 작은 원반 n-1개를 A에서 B로 이동
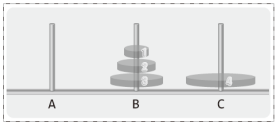	2. 큰 원반 1개를 A에서 C로 이동	2. 큰 원반 1개를 A에서 C로 이동
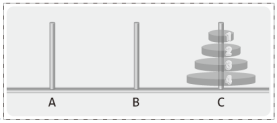	3. 작은 원반 3개를 B에서 C로 이동	3. 작은 원반 n-1개를 B에서 C로 이동

☞꼭 'A'에서 'C'로 이동하는 것이라고만 생각할게 아니라,
'원래 원반이 있던 자리'에서 '옮기고 싶은 자리'로 이동하는 것이라고 생각하자.
☞[4개-->3개-->2개-->1개]를 옮기는 문제로 점점 축소시킬 수 있고, 이는 재귀를 이용할 수 있다.

🔳 하노이 타워 문제의 해결

• 하노이 타워 함수의 기본 골격
  원반 num의 수에 해당하는 원반을 from에서 to로 이동을 시키되 그 과정에서 by를 활용한다.
  ex) HanoiTowerMove(4, 'A', 'B', 'C'); // 4개의 원반을 A-->C로 옮기되 B를 거쳐서 옮겨라

  void HanoiTowerMove(int num, char from, char by, char to)
  {
  ...
  }

• 일반화	하노이 타워 함수
  목표. 큰 원반 n개를 A에서 C로 이동	HanoiTowerMove(num, from, by, to);
  1. 작은 원반 n-1개를 A에서 B로 이동	HanoiTowerMove(num-1, from, to, by);
  2. 큰 원반 1개를 A에서 C로 이동	printf(...); //출력을 통해 확인
  3. 작은 원반 n-1개를 B에서 C로 이동	HanoiTowerMove(num-1, by, from, to);

• 구현

#include <stdio.h>

void HanoiTowerMove(int num, char from, char by, char to)
{
	if (num == 1)	//탈출조건: 이동할 원반의 수가 1개라면(남은 원반의 수가 1개라면)
	{
		printf("원반1을 %c에서 %c로 이동 \n", from, to);
	}
	else
	{
		HanoiTowerMove(num - 1, from, to, by);
		printf("원반%d을(를) %c에서 %c로 이동 \n", num, from, to);
		HanoiTowerMove(num - 1, by, from, to);
	}
}

int main() 
{
	//막대A의 원반 3개를 막대B를 경유하여 막대C로 옮기기
	HanoiTowerMove(3, 'A', 'B', 'C');
	return 0;
}

실행 결과

원반1을 A에서 C로 이동
원반2을(를) A에서 B로 이동
원반1을 C에서 B로 이동
원반3을(를) A에서 C로 이동
원반1을 B에서 A로 이동
원반2을(를) B에서 C로 이동
원반1을 A에서 C로 이동