Chap 06. 스택(Stack) [윤성우의 열혈 자료구조]

*본 내용은 [윤성우의 열혈 자료구조] 책과 강의를 보고 공부하면서 요점 정리한 내용입니다.

Chap 06-1: 스택의 이해와 ADT 정의

🔳 스택(Stack)의 이해

• 스택은 먼저 들어간 것이 나중에 나오는 자료구조로써 초코볼이 담겨있는 통에 비유할 수 있다.
• 스택은 LIFO(Last-in, First-out)구조의 자료구조이다.
• 스택의 기본 연산
  ∙ push: 데이터 삽입. (초코볼 통에 초코볼을 넣는다.)
  ∙ pop: 데이터 추출 + 삭제. (초코볼 통에서 초코볼을 꺼낸다.)
  ∙ peek: 데이터 추출. (이번에 꺼낼 초코볼의 색이 무엇인지 통 안을 들여다 본다.)

🔳 스택 ADT 정의

• ADT를 대상으로 '배열 기반의 스택' 또는 '연결 기반의 스택'을 구현할 수 있다.

• void StackInit(Stack * pstack);
  ∙ 스택의 초기화를 진행한다.
  ∙ 스택 생성 후 제일 먼저 호출되어야 하는 함수이다.

• int SIsEmpty(Stack * pstack);
  ∙ 스택이 빈 경우 TRUE(1)을, 그렇지 않은 경우 FALSE(0)을 반환한다.

• void SPush(Stack * pstack, Data data);
  ∙ 스택에 데이터를 저장한다. 매개변수 data로 전달된 값을 저장한다.

• Data SPop(Stack * pstack);
  ∙ 마지막에 저장된 요소를 삭제한다.
  ∙ 삭제된 데이터는 반환이 된다.
  ∙ 본 함수의 호출을 위해서는 데이터가 하나 이상 존재함이 보장되어야 한다.

• Data Speek(Stack * pstack);
  ∙ 마지막에 저장된 요소를 반환하되 삭제하지 않는다.
  ∙ 본 함수의 호출을 위해서는 데이터가 하나 이상 존재함이 보장되어야 한다.

Chap 06-2: 스택의 배열 기반 구현

🔳 배열 기반 스택의 논리

✔ 구현의 논리

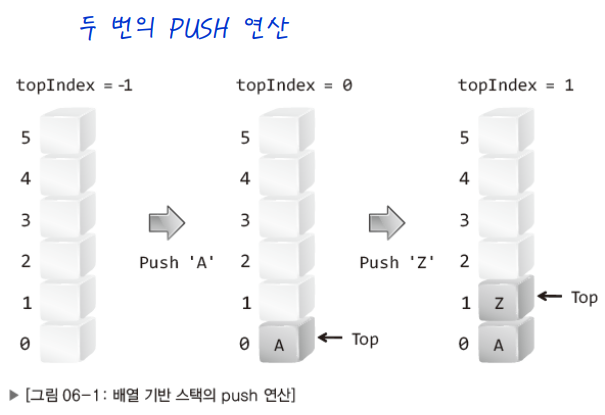
• 인덱스가 0인 위치를 스택의 바닥으로 정의해야 배열 길이에 상관없이 바닥의 인덱스 값이 동일해진다.
• 마지막에 저장된 데이터의 위치를 기억해야 한다. (topIndex)

• push: Top을 위로 한 칸 올리고, Top이 가리키는 위치에 데이터 저장
• pop: Top이 가리키는 데이터를 반환하고, Top을 아래로 한 칸 내림

🔳 배열 기반 스택의 구현

✔ 실행을 위해 필요한 파일들

• ArrayBaseStack.h
• ArrayBaseStack.c
• ArrayBaseStackMain.c

• 실행 결과
  5 4 3 2 1
  

✔ 스택의 헤더파일

#define TRUE	1
#define FALSE	0
#define STACK_LEN	100

typedef int Data;

/*** 배열 기반을 고려하여 정의된 스택의 구조체 ***/
typedef struct _arrayStack
{
	Data stackArr[STACK_LEN];
	int topIndex;
} ArrayStack;

typedef ArrayStack Stack;

void StackInit(Stack * pstack);
int SIsEmpty(Stack * pstack);

void SPush(Stack * pstack, Data data);
Data SPop(Stack * pstack);
Data SPeek(Stack * pstack);

✔ 초기화 및 기타 함수

void StackInit(Stack * pstack)
{
	pstack->topIndex = -1; // -1은 스택이 비었음을 의미
}

int SIsEmpty(Stack * pstack)
{
	if(pstack->topIndex == -1)
		return TRUE; // 비어있는 경우 TRUE를 반환
	else
		return FALSE;
}

✔ PUSH, POP, PEEK

void SPush(Stack * pstack, Data data)
{
	pstack->topIndex += 1;
	pstack->stackArr[pstack->topIndex] = data;
}

Data SPop(Stack * pstack)
{
	int rIdx;

	if(SIsEmpty(pstack))
	{
		printf("Stack Memory Error!");
		exit(-1);
	}

	rIdx = pstack->topIndex; // 인덱스값 잠시 저장
	pstack->topIndex -= 1;

	return pstack->stackArr[rIdx];
    // 삭제 후 데이터 값을 다시 0으로 만들어줄 필요 없다. top만 이동시키면 된다.
}

Data SPeek(Stack * pstack)
{
	if(SIsEmpty(pstack))
	{
		printf("Stack Memory Error!");
		exit(-1);
	}

	return pstack->stackArr[pstack->topIndex];
}

✔ main 함수

#include <stdio.h>
#include "ArrayBaseStack.h"

int main(void)
{
	// Stack의 생성 및 초기화 ///////
	Stack stack;
	StackInit(&stack);

	// 데이터 넣기 ///////
	SPush(&stack, 1);  SPush(&stack, 2);
	SPush(&stack, 3);  SPush(&stack, 4);
	SPush(&stack, 5);

	// 데이터 꺼내기 ///////
	while(!SIsEmpty(&stack)) // 비었는지 확인
		printf("%d ", SPop(&stack)); 

	return 0;
}

Chap 06-3: 스택의 연결리스트 기반 구현

🔳 연결 리스트 기반 스택의 논리

✔ 구현의 논리

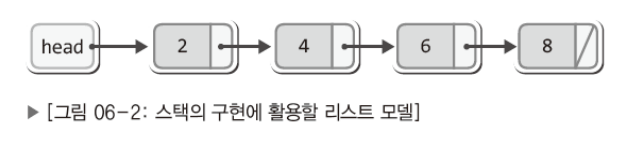
• 이렇듯 메모리 구조만 보아서는 스택임이 구분되지 않는다. 헤더파일의 정의(ADT 정의)가 중요하다.

• 저장된 순서의 역순으로 데이터(노드)를 참조(삭제)하는 연결 리스트가 바로 연결 기반의 스택이다!

• 문제 06-1에서는 CLinkedList.h와 CLinkedList.c를 바꾸지 않고 단순히 활용하여 스택의 구현을 요구한다.(연결리스트->스택 구현) 꼭 풀어보자.

🔳 연결리스트 기반 스택의 구현

✔ 실행을 위해 필요한 파일들

• ListBaseStack.h
• ListBaseStack.c
• ListBaseStackMain.c

• 실행 결과
  5 4 3 2 1
  

✔ 스택의 헤더파일

#define TRUE	1
#define FALSE	0

typedef int Data;

typedef struct _node
{
	Data data;
	struct _node * next;
} Node;

/*** 연결리스트 기반을 고려하여 정의된 스택의 구조체 ***/
typedef struct _listStack
{
	Node * head; // 헤드 하나만 있으면 된다!
} ListStack;


typedef ListStack Stack;

void StackInit(Stack * pstack);
int SIsEmpty(Stack * pstack);

void SPush(Stack * pstack, Data data);
Data SPop(Stack * pstack);
Data SPeek(Stack * pstack);

✔ 초기화 및 기타 함수

void StackInit(Stack * pstack)
{
	pstack->head = NULL;
}

int SIsEmpty(Stack * pstack)
{
	if(pstack->head == NULL)
		return TRUE;
	else
		return FALSE;
}

✔ PUSH, POP, PEEK

새 노드를 머리에 추가하고, 삭제 시 머리부터 삭제하는 단순 연결 리스트의 코드에 지나지 않는다.
연결 리스트 기반 스택을 직접 구현하는 것보다 의미 있는 것은 문제 06-1을 해결하는 것이다.

void SPush(Stack * pstack, Data data)
{
	Node * newNode = (Node*)malloc(sizeof(Node));

	newNode->data = data;
	newNode->next = pstack->head;

	pstack->head = newNode;
}

Data SPop(Stack * pstack)
{
	Data rdata;
	Node * rnode;

	if(SIsEmpty(pstack)) {
		printf("Stack Memory Error!");
		exit(-1);
	}

	rdata = pstack->head->data;
	rnode = pstack->head;

	pstack->head = pstack->head->next;
	free(rnode);

	return rdata;
}

Data SPeek(Stack * pstack)
{
	if(SIsEmpty(pstack)) {
		printf("Stack Memory Error!");
		exit(-1);
	}

	return pstack->head->data;
}

✔ main 함수

배열 기반 리스트 main함수와 완전히 동일하게 정의되었다.

#include <stdio.h>
#include "ListBaseStack.h"

int main(void)
{
	// Stack의 생성 및 초기화 ///////
	Stack stack;
	StackInit(&stack);

	// 데이터 넣기 ///////
	SPush(&stack, 1);  SPush(&stack, 2);
	SPush(&stack, 3);  SPush(&stack, 4);
	SPush(&stack, 5);

	// 데이터 꺼내기 ///////
	while(!SIsEmpty(&stack))
		printf("%d ", SPop(&stack)); 

	return 0;
}

Chap 06-4: 계산기 프로그램 구현

🔳 구현할 계산기 프로그램의 성격

• 다음과 같은 문장의 수식을 계산할 수 있어야 한다.
  ( 3 + 4 ) * ( 5 / 2 ) + ( 7 + ( 9 - 5 ) )

• 다음과 같은 문장의 수식계산을 위해서는 다음 두 가지를 고려해야 한다.
  ∙ 소괄호를 파악하여 그 부분을 먼저 연산한다.
  ∙ 연산자의 우선순위를 근거로 연산의 순위를 결정한다.

• 계산기 구현에 필요한 알고리즘은 스택과는 별개의 것이다.
  다만 그 알고리즘의 구현에 있어서 스택이 매우 요긴하게 활용된다.

🔳 세 가지 수식의 표기법: 전위, 중위, 후위

• 중위 표기법(infix notation)
  ∙ 예) 5 + 2 / 7
  ∙ 수식 내에 연산의 순서에 대한 정보가 담겨 있지 않다. 그래서 소괄호와 연산자의 우선순위라는 것을 정의하여 이를 기반으로 연산의 순서를 명시한다.

• 전위 표기법(prefix notation)
  ∙ 예) + 5 / 2 7
  ∙ 수식 내에 연산의 순서에 대한 정보가 담겨 있다. 그래서 소괄호가 필요 없고 연산의 우선순위를 결정할 필요도 없다.

• 후위 표기법(postfix notation)
  ∙ 예) 5 2 7 / +
  ∙ 전위 표기법과 마찬가지로 수식 내에 연산의 순서에 대한 정보가 담겨 있다. 그래서 소괄호가 필요 없고 연산의 우선순위를 결정할 필요도 없다.

• 소괄호와 연산자의 우선순위를 인식하게 하여 중위 표기법의 수식을 직접 계산하게 프로그래밍하는 것보다 후위 표기법의 수식을 계산하도록 프로그래밍 하는 것이 더 쉽다!

🔳 Stack을 활용한 계산기 프로그램

1. 중위 표기법 수식 → 후위 표기법 수식 변환
2. 변환된 후위 표기법 계산

🔳 1. 중위 → 후위

✔ 소괄호를 고려하지 않는 상황

1. 수식을 이루는 왼쪽 문자부터 시작해서 하나씩 처리해 나간다.
   *쟁반은 연산자를 놓는 곳(Stack)이다.

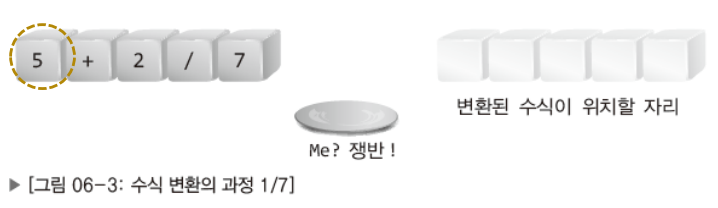
2. 피 연산자를 만나면 무조건 변환된 수식이 위치할 자리로 이동시킨다.

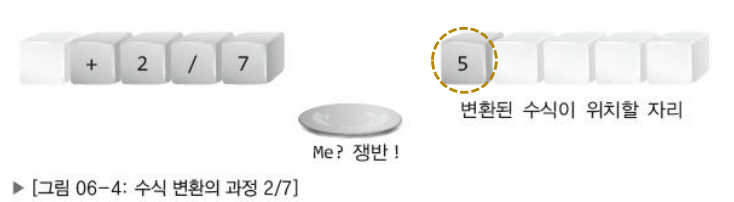
3. 연산자를 만나면 무조건 쟁반으로 이동한다.

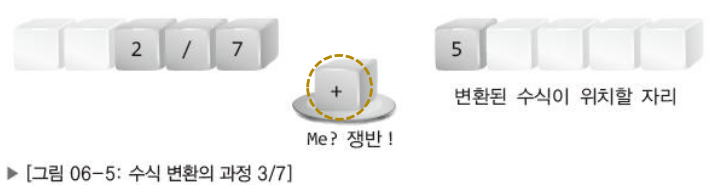
4. 숫자를 만났으니 변환된 수식이 위치할 자리로 이동!

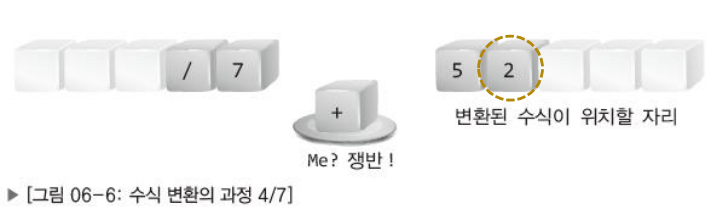
5. '/'연산자의 우선순위가 높으므로 '+' 연산자 위에 올린다.

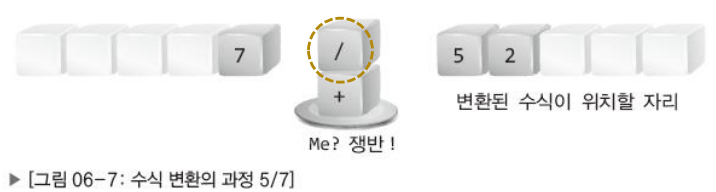
→ '/'연산자가 '+'연산자보다 먼저 사용되게 됨.

※ 쟁반에 기존 연산자가 있는 상황에서의 행동 방식

• 쟁반에 위치한 연산자의 우선순위가 높다면
  ∙ 쟁반에 위치한 연산자를 꺼내서 변환된 수식이 위치할 자리로 옮긴다.
  ∙ 그리고 새 연산자는 쟁반으로 옮긴다.
• 쟁반에 위치한 연산자의 우선순위가 낮다면
  ∙ 쟁반에 위치한 연산자의 위에 새 연산자를 쌓는다.
• 우선순위가 높은 연산자는 우선순위가 낮은 연산자 위에 올라서서 우선순위가 낮은 연산자가 먼저 자리를 잡지 못하게 하려는 목적!
• 형(우선순위↑)은 동생(우선순위↓)을 올라탈 수 있지만 동생은 형 위에 올라탈 수 없다고 생각하자.

6. 피 연산자는 무조건 변환된 수식의 자리로 이동!

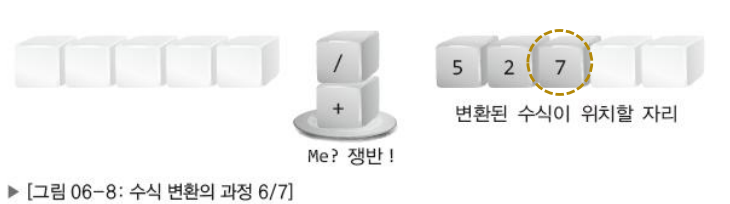
7. 나머지 연산자들은 쟁반에서 차례로 옮긴다!

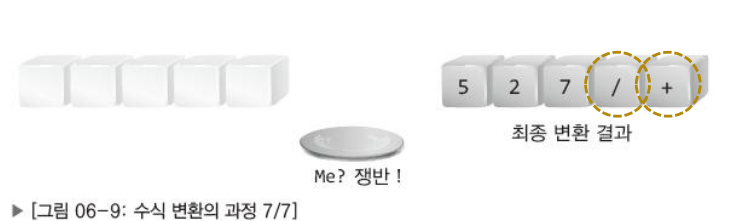
✔ 변환 규칙 정리

• 피 연산자는 그냥 옮긴다.
• 연산자는 쟁반으로 옮긴다.
• 연산자가 쟁반에 있다면 우선순위를 비교하여 처리방법을 결정한다.
• 마지막까지 쟁반에 남아있는 연산자들은 하나씩 꺼내서 옮긴다.

✔ 고민 될 수 있는 상황

• 상황 1. 연산자의 우선순위가 같은 경우
  '+' 연산자가 먼저 등장했으므로 '+' 연산자가 우선순위가 높다고 가정하고 일을 진행한다.
  (먼저 있던게 형님이다.)
  즉 '+' 연산자를 옮기고 그 자리에 '-' 연산자를 가져다 놔야 한다.

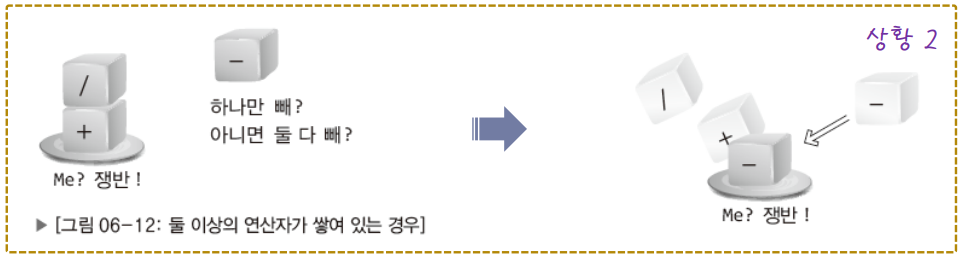
• 상황 2. 둘 이상의 연산자가 쌓여 있는 경우
  쟁반 위에 여러 연산자가 있으면 새로운 연산자와 쟁반위의 연산자들과 1대1로 비교해야 한다.

✔ 소괄호를 고려하는 상황

• 후위 표기법의 수식에서는 먼저 연산이 이뤄져야 하는 연산자가 뒤에 연산이 이뤄지는 연산자보다 앞에 위치해야 한다. 따라서 소괄호 안에 있는 연산자들이 후위 표기법의 수식에서 앞부분에 위치해야 한다.

• '(' 연산자의 우선순위는 그 어떤 사칙 연산자들보다 낮다고 간주! 그래서 ')' 연산자가 등장할 때까지 쟁반에 남아 소괄호의 경계 역할을 해야 한다.

• '(' 연산자를 만나면 쟁반(Stack)의 New 바닥이 생겼다고 생각하자. ')' 연산자를 만나면 그 바닥은 사라진다.

• ')' 연산자는 쟁반에 올릴 필요 없다.

🔳 프로그램 구현

✔ 실행을 위해 필요한 파일들

• ConvToRPNExp 함수의 선언과 정의
  ∙ InfixToPostfix.h
  ∙ InfixToPostfix.c

• 스택관련 함수의 선언과 정의
  ∙ ListBaseStack.h
  ∙ ListBaseStack.c
  

• main 함수의 정의
  ∙ InfixToPostfixMain.c

• 실행 결과
  123*+
  12+3*
  12-3+52-*
  

✔ ConvToRPNExp 함수

• ConvToRPNExp 함수는 배열exp에 담긴 중위표기법 수식을 함수의 인자로 전달받은 뒤 변환된 수식을 exp에 저장한다.
• 함수 이름의 일부인 RPN은 후위 표기법의 또 다른 이름인 Reverse Polish Notation의 약자이다.

• GetOpPrec 함수
  ∙ 함수 ConvToRPNExp의 첫 번째 helper funciton!
  ∙ 연산자의 연산 우선순위 정보를 반환한다.

int GetOpPrec(char op) 
{
	// 연산자의 우선순위에 대응하는 값을 반환한다. 값이 클수록 우선순위가 높은 것으로 정의되어 있다.
	switch(op) 
	{
	case '*':
	case '/':
		return 5; // 가장 높은 연산의 우선순위
	case '+':
	case '-':
		return 3;
	case '(': // '(' 연산자는 ')'연산자가 등장할 때까지 쟁반에 남아 있어야 하기 때문에 가장 낮은 우선순위를 부여!
		return 1;
    // ')' 연산자는 소괄호의 끝을 알리는 메시지의 역할을 한다. 따라서 쟁반으로 가지 않는다. 
    // 때문에 ')' 연산자에 대한 반환 값은 정의되어 있을 필요가 없다! 
	}

	return -1;   // 등록되지 않은 연산자
}

• WhoPrecOp 함수
  ∙ 함수 ConvToRPNExp의 두 번째 helper function!
  ∙ 두 연산자의 우선순위 비교 결과를 반환한다.
  ∙ ConvToRPNExp 함수의 실질적인 helper function이다.

int WhoPrecOp(char op1, char op2)
{
	int op1Prec = GetOpPrec(op1);
	int op2Prec = GetOpPrec(op2);

	if(op1Prec > op2Prec) // op1의 우선순위가 더 높다면
		return 1;
	else if(op1Prec < op2Prec) // op2의 우선순위가 더 높다면
		return -1;
	else // op1과 op2의 우선순위가 같다면
		return 0;
}

• ConvToRPNExp 함수

void ConvToRPNExp(char exp[])
{
	Stack stack;
	int expLen = strlen(exp);
	char * convExp = (char*)malloc(expLen+1); // 변환된 수식을 담을 공간 마련

	int i, idx=0;
	char tok, popOp;
	
	memset(convExp, 0, sizeof(char)*expLen+1); // 마련한 공간 0으로 초기화
	StackInit(&stack);

	/*** 일련의 변환 과정 ***/
	for(i=0; i<expLen; i++) // 한 숫자당 for문을 한 번씩 돈다.
	{
		tok = exp[i];
		if(isdigit(tok)) // tok에 저장된 문자가 피연산자라면
		{
			convExp[idx++] = tok;
		}
		else // tok에 저장된 문자가 연산자라면
		{
			switch(tok) // 연산자일 때의 처리 루틴
			{
			case '(': 				// 여는 소괄호라면,
				SPush(&stack, tok); // 스택에 쌓는다.
				break;

			case ')': 				// 닫는 소괄호라면,
				while(1)			// 반복해서, 
				{
					popOp = SPop(&stack);	// 스택에서 연산자를 꺼내어,
					if(popOp == '(')		// 연산자 (을 만날 때 까지,
						break;
					convExp[idx++] = popOp;	// 배열 convExp에 저장한다.
				}
				break;

			case '+': case '-': 
			case '*': case '/':
            	/*** tok에 저장된 연산자를 스택에 저장하기 위한 과정 ***/
				while(!SIsEmpty(&stack) && 
						WhoPrecOp(SPeek(&stack), tok) >= 0) 
                // Stack 맨 위 연산자의 우선순위가 높거나 같을 때 pop 한다. 
                // 연산자의 우선순위가 낮으면 반복문 종료.
					convExp[idx++] = SPop(&stack);

				SPush(&stack, tok);
				break;
			}
		}
	}

	while(!SIsEmpty(&stack)) // 스택에 남아 있는 모든 연산자를 이동시키는 반복문
		convExp[idx++] = SPop(&stack);

	strcpy(exp, convExp); // 변환된 수식을 반환
	free(convExp);
}

✔ main 함수

#include <stdio.h>
#include "InfixToPostfix.h"

int main(void)
{
	char exp1[] = "1+2*3";
	char exp2[] = "(1+2)*3";
	char exp3[] = "((1-2)+3)*(5-2)";

	ConvToRPNExp(exp1);
	ConvToRPNExp(exp2);
	ConvToRPNExp(exp3);

	printf("%s \n", exp1);
	printf("%s \n", exp2);
	printf("%s \n", exp3);
	return 0;
}

🔳 2. 후위 표기법 수식의 계산

✔ 후위 표기법 수식의 계산

• 후위 표기법은 피연산자 두 개가 연산자 앞에 항상 위치하는 구조로, 연산자를 접하면 앞 두개의 피연산자로 진행한다. 이때 지나친 숫자를 다시 꺼내는 과정에서 Stack을 활용한다.
• 예시1
  
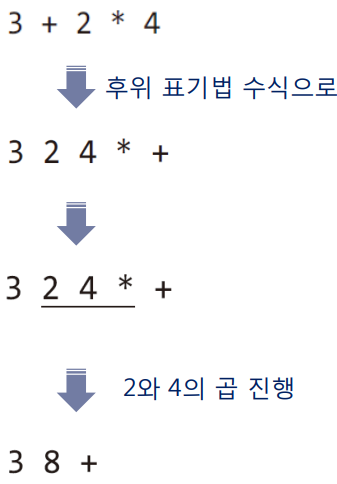
• 예시2
  

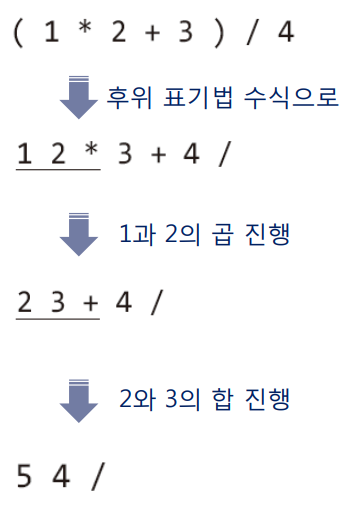
✔ 계산의 규칙

• 피 연산자는 무조건 스택으로 옮긴다.
• 연산자를 만나면 스택에서 두 개의 피연산자를 꺼내서 계산을 한다.
• 계산결과는 다시 스택에 넣는다.

🔳 프로그램 구현

✔ 실행을 위해 필요한 파일들

• EvalRPNExp 함수의 선언과 정의
  ∙ PostCalculator.h
  ∙ PostCalculator.c

• 스택관련 함수의 선언과 정의
  ∙ ListBaseStack.h
  ∙ ListBaseStack.c
  

• main 함수의 정의
  ∙ PostCalculatorMain.c

• 실행 결과
  42*8+ = 16
  123+*4/ = 1
  

✔ EvalRPNExp 함수

int EvalRPNExp(char exp[])
{
	Stack stack;
	int expLen = strlen(exp);
	int i;
	char tok, op1, op2;

	StackInit(&stack);

	for(i=0; i<expLen; i++)
	{
		tok = exp[i];

		if(isdigit(tok)) 	// 피연산자라면
		{
			SPush(&stack, tok - '0');     // 숫자로 변환하여 PUSH!
		}
		else				// 연산자라면
		{
			op2 = SPop(&stack);     // 먼저 꺼낸 값이 두 번째 피연산자!
			op1 = SPop(&stack);

			switch(tok) 
			{ // 연산 결과를 push
			case '+':
				SPush(&stack, op1+op2); 
				break;
			case '-':
				SPush(&stack, op1-op2);
				break;
			case '*':
				SPush(&stack, op1*op2);
				break;
			case '/':
				SPush(&stack, op1/op2);
				break;
			}
		}
	}
	return SPop(&stack);
}

✔ main 함수

#include <stdio.h>
#include "PostCalculator.h"

int main(void)
{
	char postExp1[] = "42*8+";
	char postExp2[] = "123+*4/";

	printf("%s = %d \n", postExp1, EvalRPNExp(postExp1));
	printf("%s = %d \n", postExp2, EvalRPNExp(postExp2));

	return 0;
}

🔳 계산기 프로그램의 완성

✔ 계산의 과정

• 중위 표기법 수식 → ConvToRPNExp(후위 표기법으로 변환) → EvalRPNExp(계산) → 연산결과

✔ 계산기 프로그램의 파일 구성

• 스택의 활용 (스택관련 함수의 선언과 정의)
  ∙ ListBaseStack.h
  ∙ ListBaseStack.c
  

• 후위 표기법의 수식으로 변환 (ConvToRPNExp 함수의 선언과 정의)
  ∙ InfixToPostfix.h
  ∙ InfixToPostfix.c
  

• 후위 표기법의 수식을 계산 (EvalRPNExp 함수의 선언과 정의)
  ∙ PostCalculator.h
  ∙ PostCalculator.c
  

• 중위 표기법의 수식을 계산
  ∙ InfixCalculator.h
  ∙ InfixCalculator.c
  

• main 함수의 정의
  ∙ InfixCalculatorMain.c

• 실행 결과
  1+2*3 = 7
  (1+2)*3 = 9
  ((1-2)+3)*(5-2) = 6
  

✔ InfixCalculator.h, InfixCalculator.c, InfixCalculatorMain.c

InfixCalculator.h

#ifndef __INFIX_CALCULATOR__
#define __INFIX_CALCULATOR__

int EvalInfixExp(char exp[]);

#endif

InfixCalculator.c

#include <string.h>
#include <stdlib.h>
#include "InfixToPostfix.h"
#include "PostCalculator.h"

int EvalInfixExp(char exp[])
{
	int len = strlen(exp);
	int ret;
	char * expcpy = (char*)malloc(len+1);	// 문자열 저장공간 마련
	strcpy(expcpy, exp);					// exp를 expcpy에 복사

	ConvToRPNExp(expcpy);    			// 후위 표기법의 수식으로 변환
	ret = EvalRPNExp(expcpy);			// 변환된 수식의 계산

	free(expcpy);			// 문자열 저장공간 해제
	return ret;				// 계산결과 반환
}

InfixCalculatorMain.c

#include <stdio.h>
#include "InfixCalculator.h"

int main(void)
{
	char exp1[] = "1+2*3";
	char exp2[] = "(1+2)*3";
	char exp3[] = "((1-2)+3)*(5-2)";

	printf("%s = %d \n", exp1, EvalInfixExp(exp1));
	printf("%s = %d \n", exp2, EvalInfixExp(exp2));
	printf("%s = %d \n", exp3, EvalInfixExp(exp3));
	return 0;
}