Chap 09. 우선순위 큐와 힙 [윤성우의 열혈 자료구조]

*본 내용은 [윤성우의 열혈 자료구조] 책과 강의를 보고 공부하면서 요점 정리한 내용입니다.

Chap 09-1: 우선순위 큐의 이해

🔳 우선순위 큐

✔ 우선순위 큐와 우선순위의 이해

• 일반 큐의 두 가지 연산
  ∙ enqueue: 큐에 데이터를 삽입하는 행위
  ∙ dequeue: 큐에서 데이터를 꺼내는 행위
  ※ 들어간 순서를 근거로 dequeue 연산이 진행된다.

• 우선순위 큐의 두 가지 연산
  ∙ enqueue: 우선순위 큐에 데이터를 삽입하는 행위
  ∙ dequeue: 우선순위 큐에서 데이터를 꺼내는 행위
  ※ 들어간 순서에 상관 없이 우선순위를 근거로 dequeue 연산이 진행된다.

• 데이터 별 우선순위의 비교기준은 프로그래머가 결정할 몫이다. 따라서 우선순위 큐 자료구조를 활용하는 프로그래머가 직접 우선순위 비교기준을 결정할 수 있도록 구현이 되어야 한다.

✔ 우선순위 큐의 구현 방법

• 우선순위 큐를 구현하는 세 가지 방법
  1) 배열을 기반으로 구현하는 방법
  2) 연결 리스트를 기반으로 구현하는 방법
  3) 힙(heap)을 이용하는 방법

• 배열, 연결리스트를 기반으로 구현하는 방법 모두 최악의 경우 새 데이터의 위치를 찾기 위해서 기존에 저장된 모든 데이터와 비교를 진행해야 한다. → 성능이 떨어진다.

🔳 힙

✔ 힙(Heap)의 소개

[힙의 조건]
1. 힙은 '완전 이진 트리' 이다.

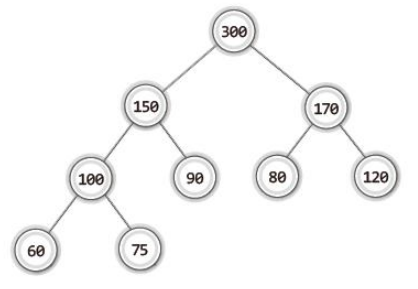
2-1. 최대 힙(max heap): 모든 노드에 저장된 값은 자식 노드에 저장된 값보다 크거나 같아야 한다. 즉 루트 노드에 저장된 값이 가장 커야 한다.

2-2. 최소 힙(min heap): 모든 노드에 저장된 값은 자식 노드에 저장된 값보다 작거나 같아야 한다. 즉 루트 노드에 저장된 값이 가장 작아야 한다.

→ '우선순위 큐'를 구현하는 적합한 자료구조가 '힙'이다.

Chap 09-2: 힙의 구현과 우선순위 큐의 완성

🔳 힙

✔ 힙에서의 데이터 저장과정

0. 최소힙
   

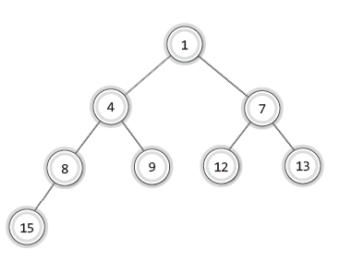
1. 새 데이터는 우선순위가 낮다는 가정하에 끝에 저장 그리고 부모 노드와 비교를 진행
   

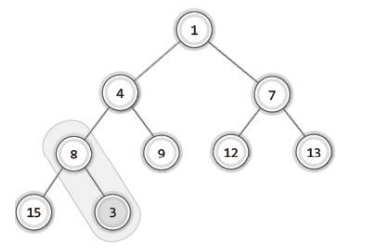
2. 부모 노드와 비교 및 자리 바꿈
   

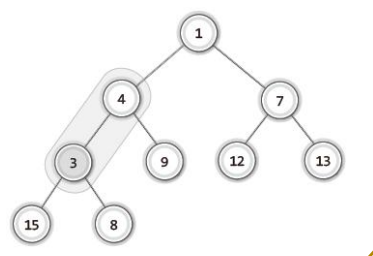
3. 제자리 찾음!
   

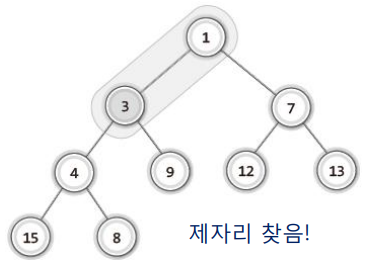
✔ 힙에서의 데이터 삭제과정

• 우리는 우선순위 큐를 구현하고자 하므로 데이터 삭제는 루트 노드의 삭제만을 말한다.

1. 루트 노드 삭제
   

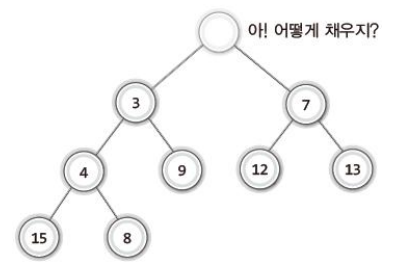
2. 마지막 노드를 루트 노드로 이동
   

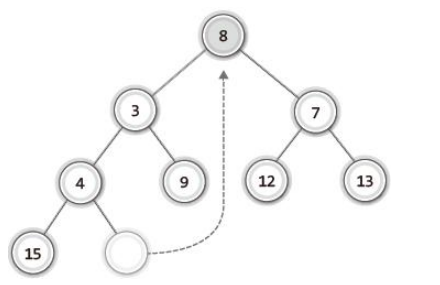
3. 자식 노드와 비교 후 이동

• 이 때 8과 3, 7 모두 비교하는게 아닌 3, 7 중 우선순위가 높은 것(3)과 비교하면 된다.

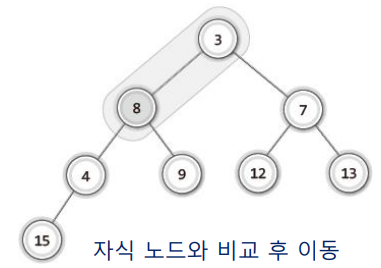
4. 자식 노드와 비교 후 자리 확정

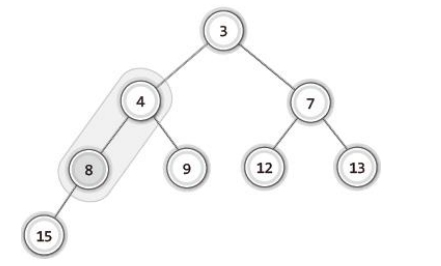
✔ 삽입과 삭제의 과정에서 보안 성능의 평가

• 배열 기반 우선순위 큐의 시간 복잡도
  ∙ 배열 기반 데이터 삽입의 시간 복잡도 $O(n)$
  ∙ 배열 기반 데이터 삭제의 시간 복잡도 $O(1)$

• 연결 리스트 기반 우선순위 큐의 시간 복잡도
  ∙ 연결 리스트 기반 데이터 삽입의 시간 복잡도 $O(n)$
  ∙ 연결 리스트 기반 데이터 삭제의 시간 복잡도 $O(1)$

• 힙 기반 우선순위 큐의 시간 복잡도
  ∙ 힙 기반 데이터 삽입의 시간 복잡도 $O(log_2 n)$
  ∙ 힙 기반 데이터 삽입의 시간 복잡도 $O(log_2 n)$

• 단 여기서 말하는 '완전 이진 트리'인 힙은 배열을 기반으로 구현한다!

🔳 원리 이해 중심의 힙 구현

✔ 배열을 기반으로 힙을 구현하는데 필요한 지식들

• 연결 리스트를 기반으로 힙을 구현하면 새로운 노드를 힙의 마지막 위치에 추가하는 것이 쉽지 않다. 그러므로 배열을 기반으로 힙을 구현해보자.

• 배열 기반에서 인덱스 값 구하기
  ∙ 왼쪽 자식 노드의 인덱스 값: 부모 노드의 인덱스 값 x 2
  ∙ 오른쪽 자식 노드의 인덱스 값: 부모 노드의 인덱스 값 x 2 + 1
  ∙ 부모 노드의 인덱스 값: 자식 노드의 인덱스 값 / 2 (※ 나눗셈은 정수형 나눗셈)

✔ 힙의 구현: 숙지할 내용

• 힙은 완전 이진트리이다.
• 힙의 구현은 배열을 기반으로 하며 인덱스가 0인 요소는 비워둔다.
• 따라서 힙에 저장된 노드의 개수와 마지막 노드의 고유번호는 일치한다.
• 노드의 고유 번호가 노드가 저장되는 배열의 인덱스 값이 된다.
• 우선순위를 나타내는 정수 값이 작을수록 높은 우선순위를 나타낸다고 가정한다.
• 배열을 기반으로 하는 경우 힙에 저장된 노드의 개수와 마지막 노드의 고유번호가 일치하기 때문에 마지막 노드의 인덱스 값을 쉽게 얻을 수 있다! 이것은 중요한 특징이다!

✔ 실행을 위해 필요한 파일들

• SimpleHeap.h
• SimpleHeap.c
• SimpleHeapMain.c

• 실행 결과
  A
  A
  B
  B
  C
  C
  

✔ 헤더파일

• '우선순위 큐'의 구현을 목적으로 하는 '힙'의 헤더파일!

typedef char HData;
typedef int Priority;

// 데이터와 우선순위 정보를 각각 구분하였음에 주목! 이것이 옳은 것만은 아니다!
typedef struct _heapElem
{
	Priority pr;	// 값이 작을수록 높은 우선순위
	HData data;
} HeapElem;

typedef struct _heap
{
	int numOfData;
	HeapElem heapArr[HEAP_LEN];
} Heap;

/*** Heap 관련 연산들 ****/
void HeapInit(Heap * ph);
int HIsEmpty(Heap * ph);

void HInsert(Heap * ph, HData data, Priority pr);
HData HDelete(Heap * ph); // 우선순위가 가자 높은 데이터 삭제되도록 정의!

#endif

✔ 초기화

// 초기화
void HeapInit(Heap * ph) 
{
	ph->numOfData = 0;
}

// 비었는지 확인
int HIsEmpty(Heap * ph)
{
	if(ph->numOfData == 0)
		return TRUE;
	else
		return FALSE;
}

✔ Helper

// 부모 노드의 인덱스 값 반환
int GetParentIDX(int idx) 
{ 
	return idx/2; 
}

// 왼쪽 자식 노드의 인덱스 값 반환
int GetLChildIDX(int idx) 
{ 
	return idx*2; 
}

// 오른쪽 자식 노드의 인덱스 값 반환
int GetRChildIDX(int idx) 
{ 
	return GetLChildIDX(idx)+1; 
}

// 우선순위가 높은 자식의 인덱스 값 반환
int GetHiPriChildIDX(Heap * ph, int idx)
{
	// 자식 노드가 존재하지 않는다면
	if(GetLChildIDX(idx) > ph->numOfData)    // numOfData는 마지막 노드의 고유번호이니, 자식 노드의 값이 이보다 크면 존재하지 않는 자식노드이다.
		return 0;

	// 자식 노드가 왼쪽 자식 노드 하나만 존재한다면
	else if(GetLChildIDX(idx) == ph->numOfData)    // 완전 이진 트리이므로 자식 노드가 하나 존재하면 이는 왼쪽 자식 노드이다.
		return GetLChildIDX(idx);

	// 자식 노드가 둘 다 존재한다면
	else  
	{
    	// 오른쪽 자식 노드의 우선순위가 높다면
		if(ph->heapArr[GetLChildIDX(idx)].pr 
						> ph->heapArr[GetRChildIDX(idx)].pr)
			return GetRChildIDX(idx); // 오른쪽 자식 노드의 인덱스 값 반환
        // 왼쪽 자식 노드의 우선순위가 높다면
		else
			return GetLChildIDX(idx); // 왼쪽 자식 노드의 인덱스 값 반환
	}
}

✔ HDelete

• 항상 그림과 코드가 같을 필요는 없다. 굳이 루트 노드의 자리로 옮기지 않아도 된다! 대신 루트 노드가 위치해야 할 인덱스 값을 저장한다.
  마지막 노드를 바로 루트 노드로 옮기지 않고 잠깐 떼어둔 상태로 비교한다. 항상 노드를 옮긴 후 비교할 필요 없다.

HData HDelete(Heap * ph)
{
	HData retData = (ph->heapArr[1]).data;    // 반환을 위해서 삭제할 데이터 저장
	HeapElem lastElem = ph->heapArr[ph->numOfData];	// 힙의 마지막 노드 저장
    // 마지막 노드를 임시 저장하여 그에 맞는 자리를 찾아나간다.

	// 아래의 변수 parentIdx에는 마지막 노드가 저장될 위치정보가 담긴다.
	int parentIdx = 1;    // 루트 노드가 위치해야 할 인덱스 값 저장
	int childIdx;

	// 루트 노드의 우선순위가 높은 자식 노드를 시작으로 반복문 시작
	while(childIdx = GetHiPriChildIDX(ph, parentIdx))
	{
		if(lastElem.pr <= ph->heapArr[childIdx].pr)	// 마지막 노드와 우선순위 비교
			break;	// 마지막 노드의 우선순위가 높으면 반복문 탈출

		// 마지막 노드보다 우선순위 높으니, 비교대상 노드의 위치를 한 레벨 올림
		ph->heapArr[parentIdx] = ph->heapArr[childIdx];
		parentIdx = childIdx;	// 마지막 노드가 저장될 위치정보를 한 레벨 내림
		// 반복문 탈출하면 parentIdx에는 마지막 노드의 위치정보가 저장됨
    }

	ph->heapArr[parentIdx] = lastElem;	// 마지막 노드 최종 저장
	ph->numOfData -= 1;
	return retData;
}

✔ HInsert

• 새 노드의 인덱스 정보를 갱신만 하자! 어차피 이동해야 하므로 그림처럼 실제 저장까지 할 필요는 없다.

void HInsert(Heap * ph, HData data, Priority pr)
{
	int idx = ph->numOfData+1;		// 새 노드가 저장될 인덱스 값을 idx에 저장 (마지막 노드의 다음 위치)
	HeapElem nelem = {pr, data}; 	// 새 노드의 생성 및 초기화

	// 새 노드가 저장될 위치가 루트 노드의 위치가 아니라면 while문 반복
	while(idx != 1)
	{
    	// 새 노드와 부모 노드의 우선순위 비교
		if(pr < (ph->heapArr[GetParentIDX(idx)].pr))	// 새 노드의 우선순위 높다면
		{
        	// 부모 노드를 한 레벨 내람, 실제로 내림
			ph->heapArr[idx] = ph->heapArr[GetParentIDX(idx)];
            
            // 새 노드를 한 레벨 올림, 실제로 올리지는 않고 인덱스 값만 갱신
			idx = GetParentIDX(idx);
		}
		else	// 새 노드의 우선순위가 높지 않다면
			break;
	}
	
	ph->heapArr[idx] = nelem;	// 새 노드를 배열에 저장
	ph->numOfData += 1;
}

✔ main 함수

int main(void)
{
	Heap heap;
	HeapInit(&heap);	// 힙의 초기화

	HInsert(&heap, 'A', 1);	// 문자 'A'를 최고의 우선순위로 저장
	HInsert(&heap, 'B', 2);	// 문자 'B'를 두 번째 우선순위로 저장
	HInsert(&heap, 'C', 3);	// 문자 'C'를 세 번째 우선순위로 저장
	printf("%c \n", HDelete(&heap));

	HInsert(&heap, 'A', 1);	// 문자 'A' 한 번 더 저장
	HInsert(&heap, 'B', 2);	// 문자 'B' 한 번 더 저장
	HInsert(&heap, 'C', 3);	// 문자 'C' 한 번 더 저장
	printf("%c \n", HDelete(&heap));

	while(!HIsEmpty(&heap))
		printf("%c \n", HDelete(&heap));

	return 0;
}

• 하지만 데이터를 저장할 때 우선순위 정보를 별도로 전달하는 것은 적합하지 않은 경우가 많다. 일반적으로 데이터의 우선순위는 데이터를 근거로 판단이 이뤄지기 때문이다.

🔳 제법 쓸만한 수준의 힙 구현

✔ 실행을 위해 필요한 파일들

• UsefulHeap.h
• UsefulHeap.c
• UsefulHeapMain.c

• 실행 결과
  A
  A
  B
  B
  C
  C
  

✔ 구조체 변경

• 프로그래머가 힙의 우선순위 판단 기준을 설정할 수 있어야 한다.
• 구조체의 변경

typedef struct _heapElem
{
	Priority pr;
	HData data;
} HeapElem;

typedef struct _heap
{
	int numOfData;
	HeapElem heapArr[HEAP_LEN];
} Heap;
	
    		↓

// 우선순위를 별도로 저장하지 않고자 한다.
typedef struct _heap
{
	PriorityComp * comp; // 우선순위 판단하는 함수의 주소값
	int numOfData;
	HData heapArr[HEAP_LEN];
} Heap;

※ typedef int PriorityComp(HData d1, HData d2); 로 선언했다면 힙 구조체 내에서 PriorityComp * comp;로,
typedef int (*PriorityComp)(HData d1, HData d2); 로 선언했다면 힙 구조체 내에서 PriorityComp comp;로 작성한다.

• 초기화 함수의 변경

void HeapInit(Heap * ph) 
{
	ph->numOfData = 0;
}
    		↓
void HeapInit(Heap * ph, PriorityComp pc) // (힙 주소값, 우선순위정보함수 주소값) 
{
	ph->numOfData = 0;	// 초기화
	ph->comp = pc;		// 함수 등록
}

✔ PriorityComp

• PriorityComp형 함수의 정의 기준
  ∙ 첫 번째 인자의 우선순위가 높다면, 0보다 큰 값 반환
  ∙ 두 번째 인자의 우선순위가 높다면, 0보다 작은 값 반환
  ∙ 첫 번째, 두 번째 인자의 우선순위가 동일하다면, 0 반환

• PriorityComp형 함수가 등록되면 HInsert 함수는 등록된 함수를 활용하여 우선순위를 비교 판단한다.

void HInsert(Heap * ph, HData data, Priority pr);
    		↓
void HInsert(Heap * ph, HData data); // 우선 순위 정보를 별도로 받지 않는다.

✔ Helper 함수의 변경

• comp에 등록된 함수의 호출결과를 통해서 우선순위를 판단한다.

int GetHiPriChildIDX(Heap * ph, int idx)
{
	if(GetLChildIDX(idx) > ph->numOfData)
		return 0;

	else if(GetLChildIDX(idx) == ph->numOfData)
		return GetLChildIDX(idx);

	else
	{
	//	if(ph->heapArr[GetLChildIDX(idx)].pr 
	//				> ph->heapArr[GetRChildIDX(idx)].pr)
		if(ph->comp(ph->heapArr[GetLChildIDX(idx)], 
					ph->heapArr[GetRChildIDX(idx)]) < 0)
			return GetRChildIDX(idx);
		else
			return GetLChildIDX(idx);
	}
}

✔ HInsert의 변경

• comp에 등록된 함수의 호출결과를 통해서 우선순위를 판단한다.

void HInsert(Heap * ph, HData data)
{
	int idx = ph->numOfData+1;

	while(idx != 1)
	{
	//	if(pr < (ph->heapArr[GetParentIDX(idx)].pr))
		if(ph->comp(data, ph->heapArr[GetParentIDX(idx)]) > 0)
		{
			ph->heapArr[idx] = ph->heapArr[GetParentIDX(idx)];
			idx = GetParentIDX(idx);
		}
		else
		{
			break;
		}
	}
	
	ph->heapArr[idx] = data;
	ph->numOfData += 1;
}

✔ HDelete의 변경

• comp에 등록된 함수의 호출결과를 통해서 우선순위를 판단한다.

HData HDelete(Heap * ph)
{
	HData retData = ph->heapArr[1];
	HData lastElem = ph->heapArr[ph->numOfData];

	int parentIdx = 1;
	int childIdx;

	while(childIdx = GetHiPriChildIDX(ph, parentIdx))
	{
	//	if(lastElem.pr <= ph->heapArr[childIdx].pr)
		if(ph->comp(lastElem, ph->heapArr[childIdx]) >= 0)
			break;

		ph->heapArr[parentIdx] = ph->heapArr[childIdx];
		parentIdx = childIdx;
	}

	ph->heapArr[parentIdx] = lastElem;
	ph->numOfData -= 1;
	return retData;
}

✔ main 함수

#include <stdio.h>
#include "UsefulHeap.h"

int DataPriorityComp(char ch1, char ch2)
{
	return ch2-ch1;	// 아스키코드 값이 작은 문자의 우선순위가 더 높다! 
//	return ch1-ch2; // 반대의 경우
}

int main(void)
{
	Heap heap;
	HeapInit(&heap, DataPriorityComp);

	HInsert(&heap, 'A');
	HInsert(&heap, 'B');
	HInsert(&heap, 'C');
	printf("%c \n", HDelete(&heap));

	HInsert(&heap, 'A');
	HInsert(&heap, 'B');
	HInsert(&heap, 'C');
	printf("%c \n", HDelete(&heap));

	while(!HIsEmpty(&heap))
		printf("%c \n", HDelete(&heap));

	return 0;
}

• 실행결과

A
A
B
B
C
C

🔳 우선순위 큐의 완성

✔ 제법 쓸만한 수준의 힙을 이용한 우선순위 큐의 구현

• 힙의 함수를 사실상 우선순위 큐의 내용으로 구현해 놓았기 때문에 실제 할 일은 별 것 없다!

PriorityQueue.h

#ifndef __PRIORITY_QUEUE_H__
#define __PRIORITY_QUEUE_H__

#include "UsefulHeap.h"

typedef Heap PQueue;
typedef HData PQData;

void PQueueInit(PQueue * ppq, PriorityComp pc);
int PQIsEmpty(PQueue * ppq);

void PEnqueue(PQueue * ppq, PQData data);
PQData PDequeue(PQueue * ppq);

#endif

PriorityQueue.c

#include "PriorityQueue.h"
#include "UsefulHeap.h"

void PQueueInit(PQueue * ppq, PriorityComp pc)
{
	HeapInit(ppq, pc);
}

int PQIsEmpty(PQueue * ppq)
{
	return HIsEmpty(ppq);
}

void PEnqueue(PQueue * ppq, PQData data)
{
	HInsert(ppq, data);
}

PQData PDequeue(PQueue * ppq)
{
	return HDelete(ppq);
}

PriorityQueueMain.c

#include <stdio.h>
#include "PriorityQueue.h"

int DataPriorityComp(char ch1, char ch2)
{
	return ch2-ch1;
}

int main(void)
{
	PQueue pq;
	PQueueInit(&pq, DataPriorityComp);

	PEnqueue(&pq, 'A');
	PEnqueue(&pq, 'B');
	PEnqueue(&pq, 'C');
	printf("%c \n", PDequeue(&pq));

	PEnqueue(&pq, 'A');
	PEnqueue(&pq, 'B');
	PEnqueue(&pq, 'C');
	printf("%c \n", PDequeue(&pq));

	while(!PQIsEmpty(&pq))
		printf("%c \n", PDequeue(&pq));

	return 0;
}