시간복잡도 속도비교
O(1) < O(logN) < O(N) < O(N*logN) < O(N^2) < O(2^N) < O(N!)
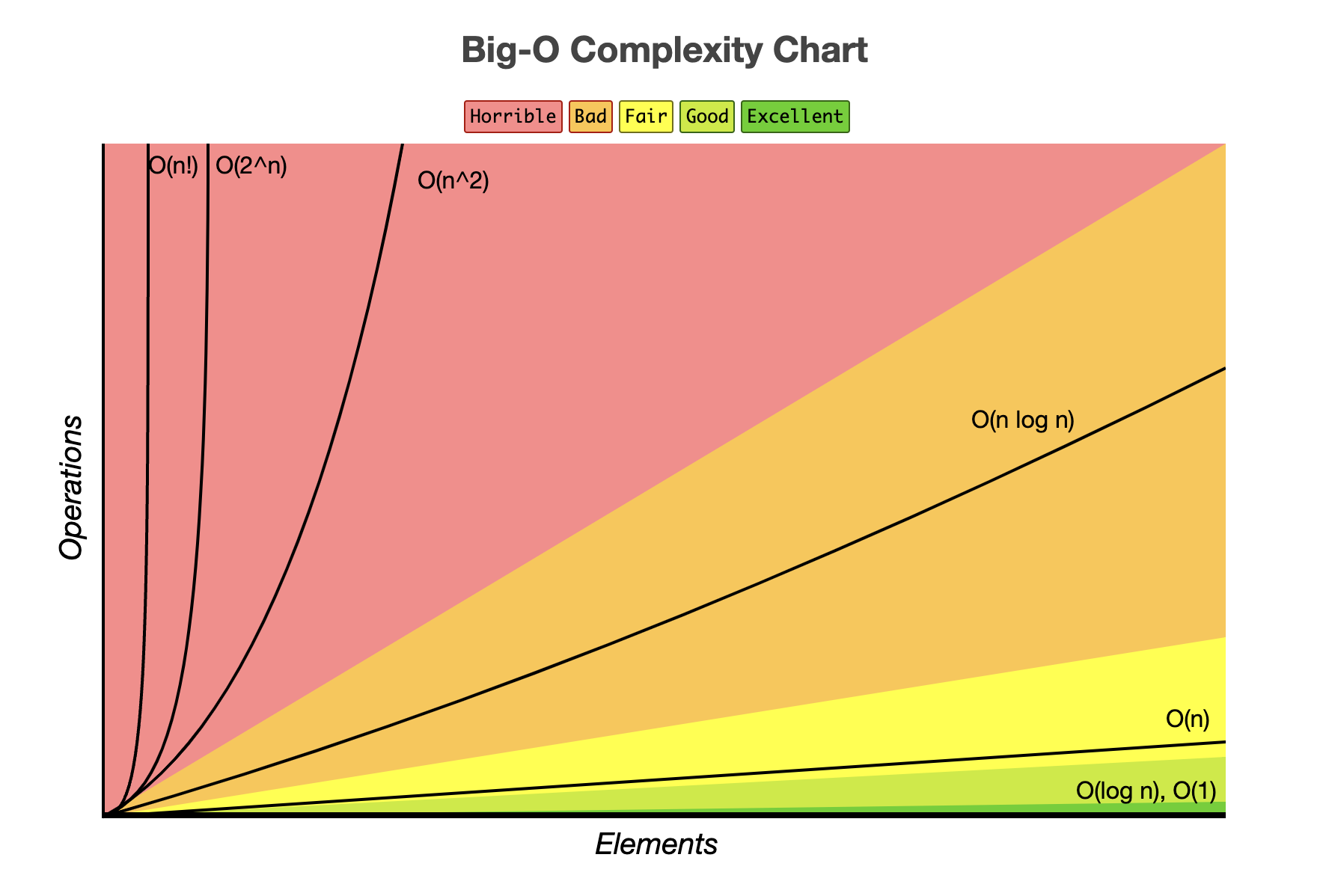
[이미지 출처] https://www.bigocheatsheet.com/
백준에서의 시간복잡도 (코테에서의 시간복잡도)
백준은 문제에서 데이터 크기를 통해 시간복잡도를 암시한다.
문제를 풀기 전 문제가 요구하는 시간복잡도를 미리 계산할 수 있다.
시간복잡도를 계산할 때 보통 1초에 1억(10^8)번 연산이 가능하다고 보고 계산한다.(파이썬은 1초에 2000만번)
시간 제한: 1초
첫째 줄에 수열의 길이 n이 주어진다. n은 1보다 크고 10,000보다 작은 자연수이다.
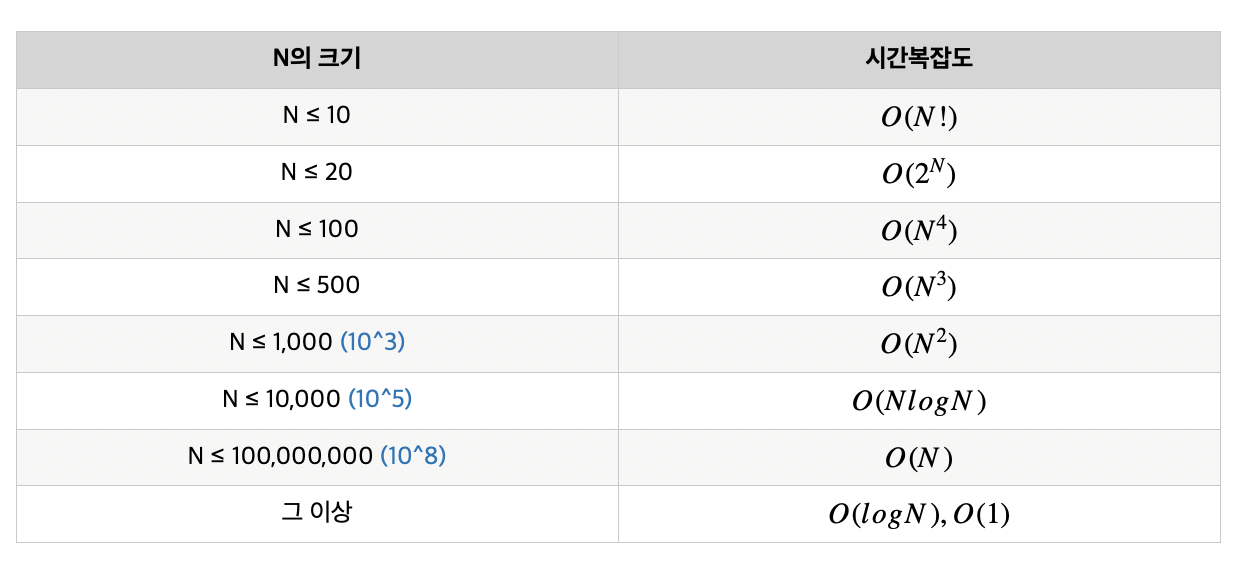
위와 같은 문제에선 1초가 주어졌으므로 총 1억(10^8)번 연산이 가능하다.
n = 10,000 일 때 O(nlogn) = O(40000)이다. 이는 1억보다 작으므로 가능하다. 만약 n이 10^8일때는 시간을 초과하므로 이 문제는 O(nlogn)의 문제풀이를 요구하는 문제이다.
시간 제한이 1초인 문제의 경우, 입력 개수에 따라 허용되는 시간복잡도는 다음과 같다.
(다음 표는 맹신하지말고 참고만)
외우면 편한 것들
- sort(): O(nlogn)
- Hashtable 구축: O(n)
- 이진탐색: O(logn)
- Heap(priority queue)
--> 길이가 n인 배열을 Heap으로 만들 때: O(nlogn)
--> push(): O(logn)
--> pop(): O(logn)
Java 실행시간 측정하는 코드
long beforeTime = System.currentTimeMillis(); // 코드 실행 전 시간
// 코드
long afterTime = System.currentTimeMillis(); // 코드 실행 후 시간
long secDiffTime = (afterTime - beforeTime)/1000; // 두 시간 차 계산
System.out.println("실행 시간(m): "+secDiffTime);자료구조에 따른 시간복잡도
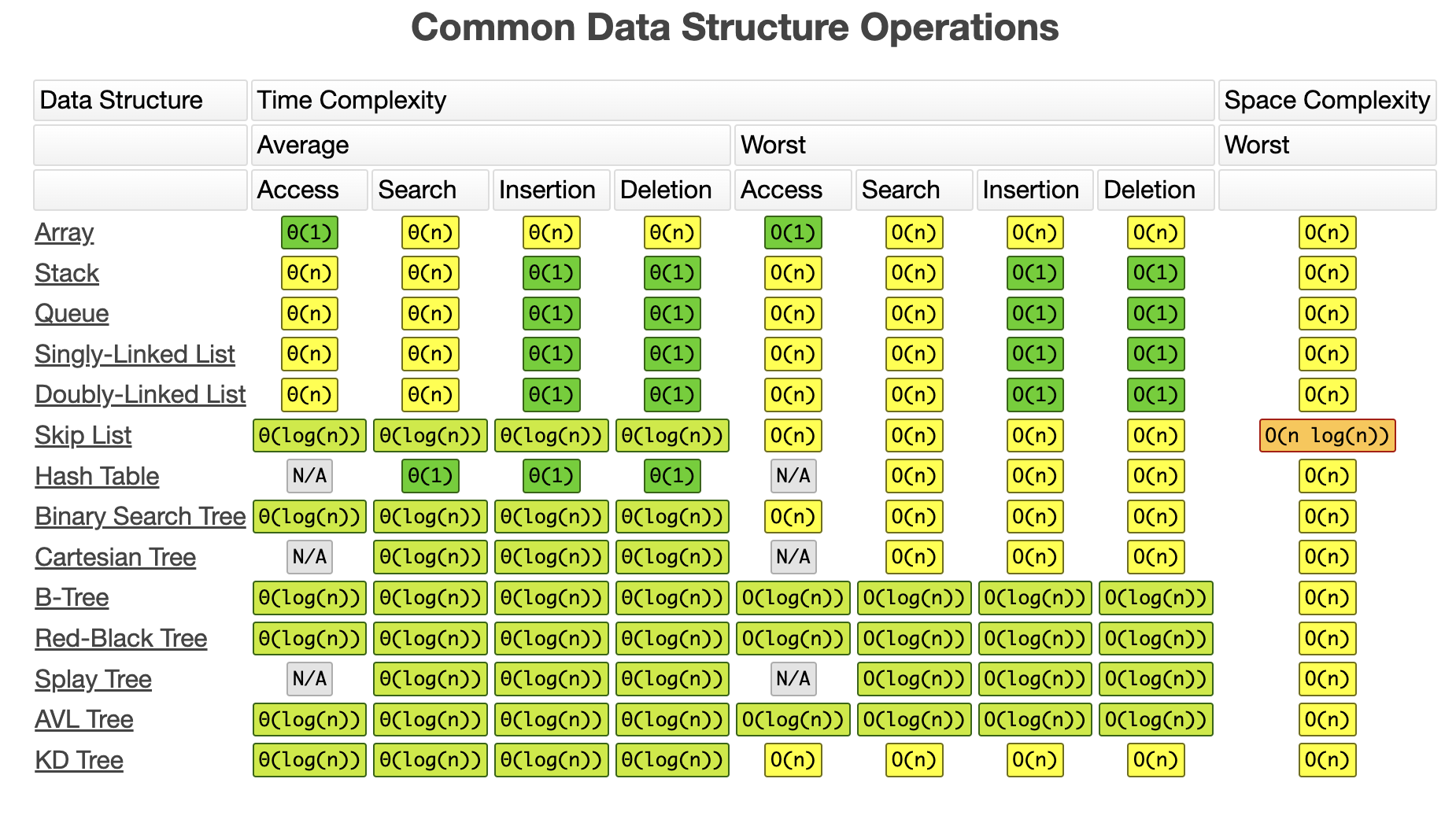
[이미지 출처] https://www.bigocheatsheet.com/
각 정렬알고리즘별 시간복잡도
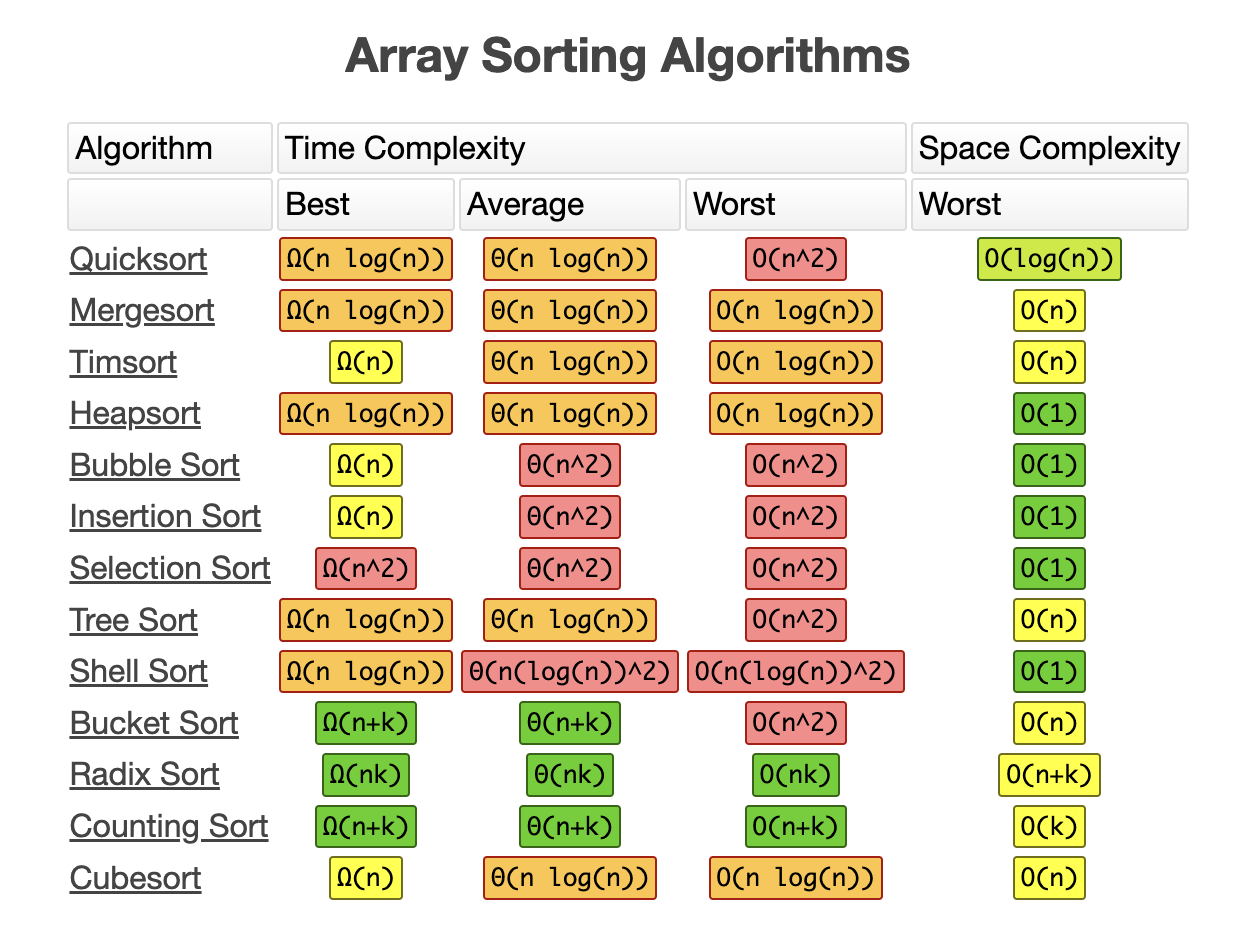
[이미지 출처] https://www.bigocheatsheet.com/
참고 자료
https://www.youtube.com/watch?v=tTFoClBZutw 시간복잡도(time complexity)를 알차게 설명합니다! 빅 오(Big O)를 포함해서 점근적 표기법을 다양한 예제와 함께 설명하니까요 들러보세요~ :)
https://www.youtube.com/watch?v=PFKPdjdWbQ8 코딩 테스트, 당신이 몰랐던 10^8가지 사실
https://invrtd-h.tistory.com/50
https://www.nossi.dev/cote/timecomplexity
