RED - BLACK TREE

가장 유명하고 많이 사용되는 균형이진탐색트리

RB트리의 조건

1. node는 red / black으로 이루어져야 함.
2. root node는 black.
3. leaf node(NIL 또는 NULL node) 역시 black.
4. red node의 자식은 무조건 black node.
   (black node의 자식 색깔은 상관없음)
5. 각 node에서 leaf node로 가는 모든 경로에서 거쳐가는 black node의 수가 항상 같아야 한다.
   RB tree의 시간 복잡도가 O(logN)임을 증명하는 성질

증명

h(v) = v의 높이(height)
bh(v) = v -> leaf nodes로 갈 때 v를 제외하고 만나는 black node의 개수

사실1: v의 서브트리의 내부 노드 개수 >= 2^bh(v) - 1

증명: h(v)에 대한 수학적 귀납법

base case:
h(v) = 0 일때, 다시말해 leaf node 하나밖에 없을 때 bh(v) = 0.
이 때 v의 서브트리의 내부노드 개수 >= 2^bh(v) -1 이고 0 >= 1-1 이므로 참이다.
내부 노드는 서브 트리 내에서 NIL노드를 제외한 모든 노드를 뜻한다.

가정:
h(v) <= K일 때 v의 서브트리의 내부 노드 개수 >= 2^bh(v) - 1 이라 가정.

증명:
h(v) = K + 1 일 때 위의 가정이 성립함을 증명함.

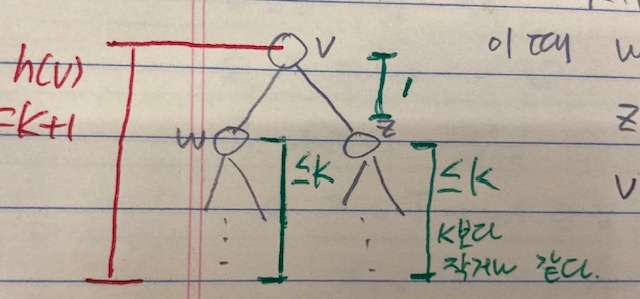
이 때 노드 v의 자식 노드로 w와 z가 존재할 때,
노드 w의 서브트리의 내부 노드 가수는 가정에 따르면 최소한 2^bh(w) - 1개 이상,
노드 z의 서브트리의 내부 노드 개수는 $2^bh(z)-1$개 이상이다.
이 때 노드 V의 서브트리의 내부 노드 개수는 (2^bh(w) - 1) + (2^bh(z) - 1) + 1 개 이상이다. (뒤에 붙는 +1은 노드 v) <w개수 + z개수 + v>

이 때 bh(w)와 bh(z)는 bh(v) 또는 bh(v) - 1 둘 중 하나와 값이 같다.
다시 말해 bh(w), bh(z) >= bh(v) - 1이다.
w가 빨간색 노드라면 bh(w) = bh(v)일 것이고, w가 검은색 노드라면 bh(w) = bh(v) - 1일 것이다.

즉,

V의 서브트리의 내부 노드의 개수 >= 2 * 2^(bh(v)-1) - 1
						    >= 2^bh(v) - 1 이 성립한다.

사실2: RB tree의 node의 갯수 >= 2^(h/2) - 1

RB tree에서 어떠한 경로를 root에서 NIL 까지 지났을 때, root도 black, red node 다음에도 반드시 black이 오므로, 이 경로 상 블랙노드의 개수는 무조건 높이의 절반 이상이다.
즉, bh(root) >= h/2라고 쓸 수 있으며 이는 앞서 한 증명과 결합했을 때

RB tree 내의 노드의 갯수 >= 2^bh(root) - 1
					   >= 2^(h/2) - 1
즉 노드의 갯수 n >= 2^(h/2) - 1 이 성립한다.

이 식을 변형시키면
2^(h/2) <= n + 1
h/2 <= $log_{2}(n+1)$
$h <= 2log_{2}(n+1)$ 이 되므로 $O(log_{2}n)$ 된다.

즉, RB트리의 시간 복잡도는 O(log n)이 되어서 매우 빠르다는 것이다.