문제
- Minimum Time Visiting All Points
User Accepted:2691
User Tried:2850
Total Accepted:2756
Total Submissions:3548
Difficulty:Easy
On a 2D plane, there are n points with integer coordinates points[i] = [xi, yi]. Return the minimum time in seconds to visit all the points in the order given by points.
You can move according to these rules:
In 1 second, you can either:
move vertically by one unit,
move horizontally by one unit, or
move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in 1 second).
You have to visit the points in the same order as they appear in the array.
You are allowed to pass through points that appear later in the order, but these do not count as visits.
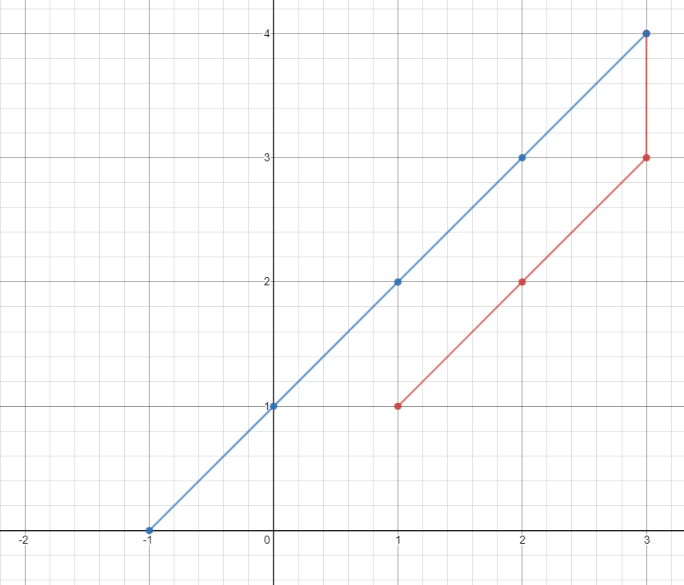
Example 1:
Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is
[1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
Time from [1,1] to [3,4] = 3 seconds
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds
Example 2:
Input: points = [[3,2],[-2,2]]
Output: 5
Constraints:
points.length == n
1 <= n <= 100
points[i].length == 2
-1000 <= points[i][0], points[i][1] <= 1000풀이
class Solution:
def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
step = 0
for i in range(len(points) - 1):
step += max(abs(points[i][0] - points[i+1][0]), abs(points[i][1] - points[i+1][1]))
return step문제를 막상 봤을 때 복잡하게 생각하기 쉽지만, 대각선으로 가는 것도 1스텝으로 치기 때문에 갈 수 있는 부분까지 최대한 대각선(또는 1 혹은 -1의 기울기)으로 간 다음, 가로나 세로를 가는 것이 점과 점 사이를 최소한의 스텝으로 움직이는 방법이다.
