[프로그래머스] 롤케이크 자르기 - JAVA [자바]

링크

문제

생각보다 나이브한 풀이도 쉽게 풀리는 문제다.

구현 + 완탐 문제..?

대충 각 인덱스마다 왼쪽과 오른쪽이 몇 종류씩 있는지를 체크하면 된다.

Set을 이용한 풀이와 counting 배열을 이용한 풀이를 준비했다.

import java.util.*;

class Solution {

    public int solution(int[] topping) {
        int[] prefix = new int[topping.length];
        int[] suffix = new int[topping.length];
        Set<Integer> set = new TreeSet<>();
        for (int i = 0; i < topping.length; i++) {
            set.add(topping[i]);
            prefix[i] = set.size();
        }
        set.clear();
        for (int i = topping.length - 1; i >= 0; i--) {
            set.add(topping[i]);
            suffix[i] = set.size();
        }
        int count = 0;
        for (int i = 0; i < topping.length - 1; i++) {
            if (prefix[i] == suffix[i + 1]) {
                count++;
            }
        }
        return count;
    }
}

set에 각 인덱스로 들어오는 숫자를 넣었을 때 set의 크기(몇 종류인지)를 저장한다.
중요한 점은 왼쪽은 왼쪽부터, 오른쪽은 오른쪽부터 넣어야 한다는 점이다. 그냥 누적합 문제를 풀 때 prefix, suffix라는 용어를 사용했어서 네이밍을 이렇게 했다.

마지막에 prefix[i] == suffix[i + 1]인 경우를 세면 된다. 예시를 통해 이를 이해해보면

index:    0 1 2 3 4 5 6 7
topping:  1 2 1 3 1 4 1 2
prefix:   1 2 2 3 3 4 4 4
suffix:   4 4 4 4 3 3 2 1

index가 3,4인 경우가 답이다.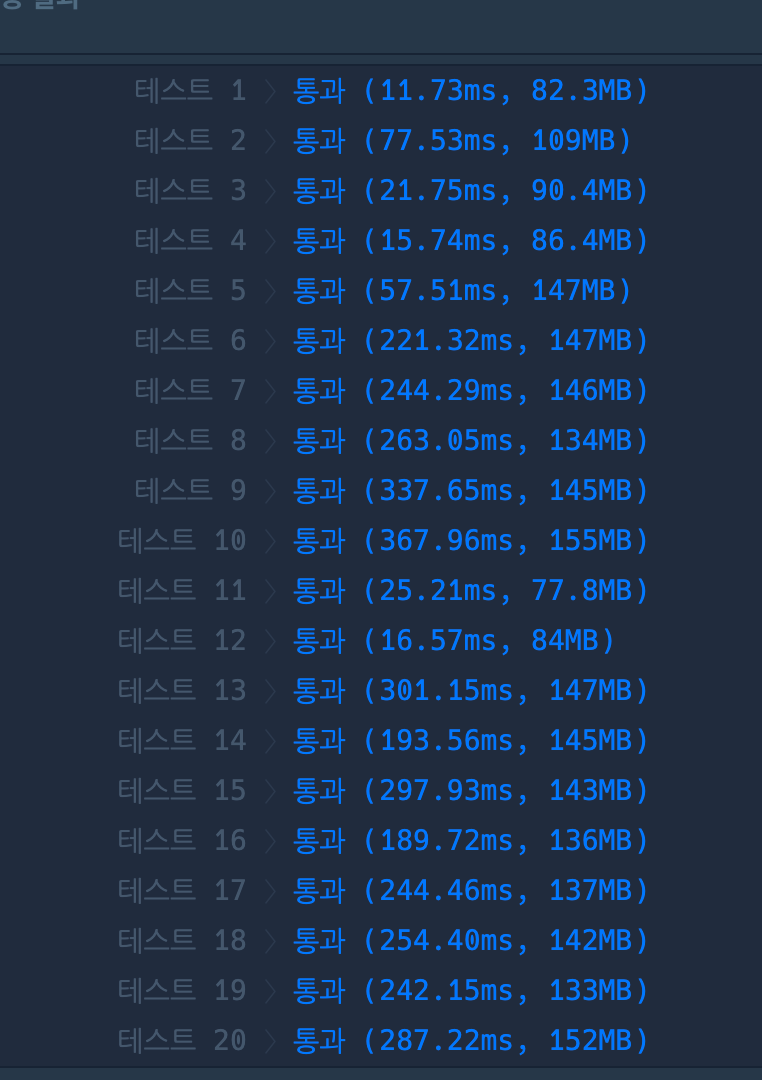

이제 counting 배열을 이용한 풀이를 보자.

class Solution {

    public int solution(int[] topping) {
        int[] left = new int[10001];
        int[] right = new int[10001];
        int r = 0;
        for (int x : topping) {
            if (right[x] == 0) {
                r++;
            }
            right[x]++;
        }
        int ans = 0;
        int l = 0;
        for (int x : topping) {
            if (right[x] == 1) {
                r--;
            }

            if (left[x] == 0) {
                l++;
            }
            right[x]--;
            left[x]++;

            if (l == r) {
                ans++;
            }
        }
        return ans;
    }
}

토핑의 종류는 최대 10000이므로 10001 크기의 counting 배열을 만들어서 풀었다.
left는 0->1 이 되는 것을 감지해서 왼쪽 종류를 증가시키고, right는 1->0이 되는 것을 감지해서 오른쪽 종류를 감소시킨다.
직관적인 풀이이므로 둘다 이해가 잘 될 것 같다.

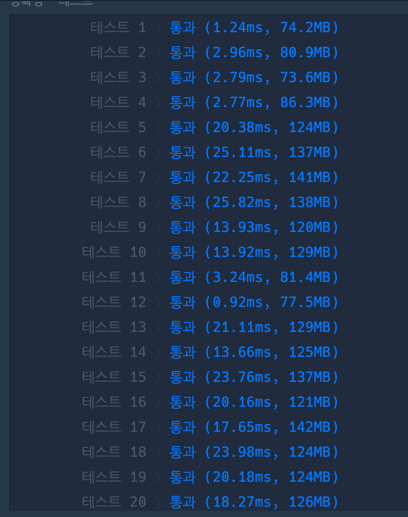
결과는 뭐 압도적으로 counting 배열이 빠르다.