딥러닝 기초2

개요

• 타이타닉 데이터를 이용한 간단한 딥러닝 실습
• Perceptron이란?

1. 타이타닉 데이터를 이용한 실습

• 전처리 및 결측치 처리 과정은 생략

  순서

  1. 모델생성
  2. model.add(출력, Dense(출력층, 활성화 함수relu, 입력shape)) 모델층 쌓기
  3. model.summary()
  4. model.compile(옵티마이저, 손실함수, 지표)

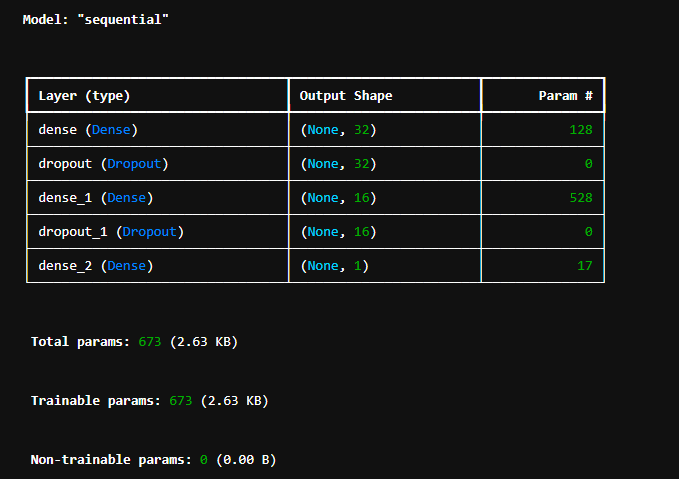
model = Sequential()
model.add(Dense(32, activation='relu', input_shape=(3,)))
model.add(Dropout(0.1)) #드롭out이라서 출력값이 0출력
model.add(Dense(16, activation='relu'))
model.add(Dropout(0.1)) #드롭out이라서 출력값이 0출력
model.add(Dense(1, activation='sigmoid'))


model.summary()

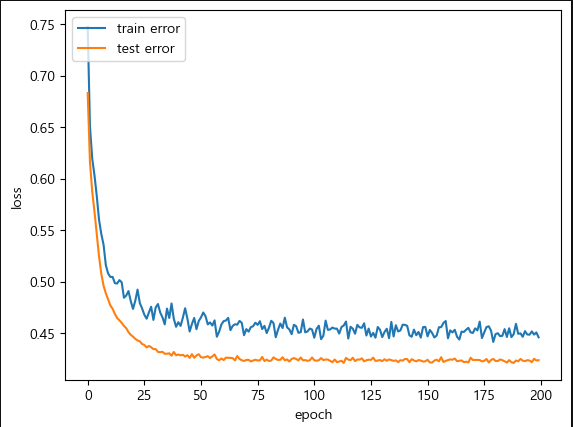
history = model.fit(tr, tr_lable, validation_data=(ts,ts_lable), batch_size=30, epochs=200, verbose=2)
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss'] 
acc = history_dict['accuracy']

pred = model.predict(ts).reshape(ts.shape[0])
pred =  np.where(pred > 0.5, 1, 0)
accuracy =  1- ( np.where((pred - ts_lable) == 0, 0, 1).sum()/len(ts_lable)) 

# 시각화 
plt.plot(loss_values)
plt.plot(val_loss_values)
plt.xlabel("epoch")
plt.ylabel('loss')
plt.legend(['train error', 'test error'], loc = 'upper left')
plt.show()

model.summary()

시각화 결과

Perceptron(퍼셉트론)

• 인공신경망의 한 종류
• 1957년 코넬 항공 연구소의 프랑크 로젠블라트(Frank Rosenblatt)에 의해 고안됨
• 다수의 신호를 받아 하나의 신호를 출력함 (인공 뉴런, 단순 퍼셉트론)
• 단층 퍼셉트론으로는 XOR의 문제를 해결이 불가능 하다는 단점이 있음 -> 직선 하나로 나눈 영역만 표현 가능하다는 한계가 있음

python 퍼셉트론 간단한 실습

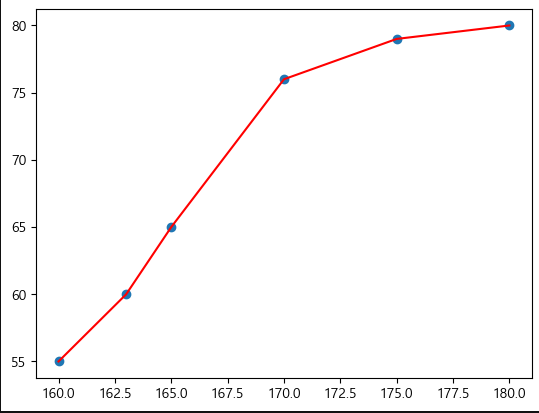
• 키 몸무게 데이터를 이용한 성별 예측
• 0: 여성 1: 남성

x = np.array( 
    [ [157,55],
      [163,60],
      [165,65],
      [170,76],
      [175,79],
      [180,80]] )
y = np.array( [0,0,0,1,1,1] ) #성별예측

# 퍼셉트론 모델 학습 
clf = Perceptron()
clf.fit(x,y)

# 시각화
plt.scatter(x[:, 0],x[:,1])
plt.plot(x[:,0],x[:,1], color = 'red')
plt.show()

# 예측처리
predicted = clf.predict(x[:])
predicted

woman = clf.predict( [[162,57] ])
print('[162,57] 대상은 ', woman)
man = clf.predict( [[174,76] ])
print('[174,76] 대상은 ', man)

시각화 결과

출력 결과
[162,57] 대상은 [0][174,76] 대상은 [1]

Multi Layer Perceptron(다층 퍼셉트론)

• 퍼셉트론을 여러층 쌓은 순방향 인공 신경망
• 입력층, 은닉층, 출력층으로 구성됨
• 각 층에서 활성함수를 통해 입력을 처리함

활성화 함수

• 입력 신호의 총 합을 출력 신호로 변환하는 함수
• 딥러닝 신경망에서 뉴런의 출력값을 결정하는 함수

  활성화 함수 종류

  함수 이름	수식/정의	출력 범위	특징 및 용도
  계단 함수	f(x) = 1 if x > 0 else 0	{0, 1}	이진 분류 개념에서 사용. 신경망 학습에는 사용 X (미분 불가)
  시그모이드	f(x) = 1 / (1 + e-x)	(0, 1)	출력값을 확률처럼 사용. 이진 분류 출력층에서 사용. 기울기 소실 문제 있음
  ReLU	f(x) = max(0, x)	[0, ∞)	계산 빠르고 대부분의 은닉층에서 기본적으로 사용. 음수 입력은 0 출력
  Tanh	f(x) = (ex - e-x) / (ex + e-x)	(-1, 1)	시그모이드보다 중심이 0이라 학습이 더 안정적. 은닉층에 사용됨
  Softmax	f(xi) = exp(xi) / Σexp(xj)	(0, 1), 합=1	다중 분류 출력층에서 사용. 각 클래스 확률을 출력하며 합은 1이 됨

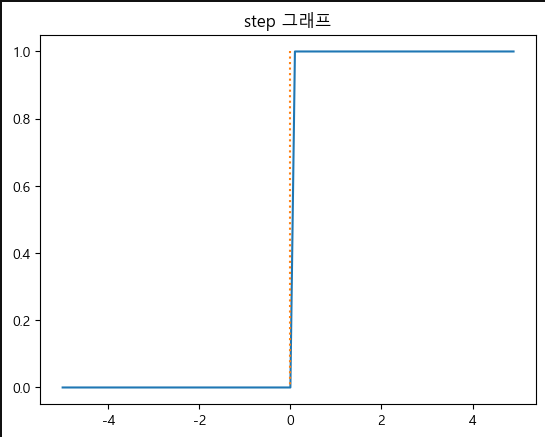
계단 함수 (Step Function)

• 입력값이 0보다 크면 1, 그외에는 0을 출력하는 이진 분류 함수
• 출력이 0,1 만 가능
• 매우 직관적임

  식

  $f(x) = \begin{cases} 1, & \text{if } x > 0 \\ 0, & \text{otherwise} \end{cases}$

def step(x):
    y = x > 0
    return y
# 계단함수 그래프 시각화 
x = np.arange(-5.0, 5.0, 0.1)
y = step(x)
plt.plot(x,y)
plt.plot([0,0], [1.0, 0.0], ':')
plt.title('step 그래프')
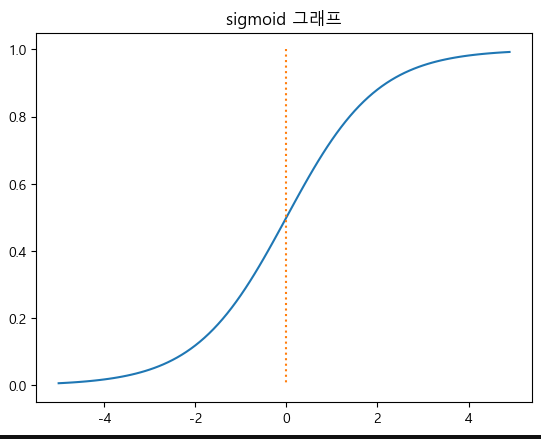
plt.show()

시그모이드 함수 (Sigmoid Function)

• 입력값을 0에서 1 사이의 확률 값처럼 변환하는 연속적인 S자 형태 함수
• 이진 분류의 출력층에서 사용
• 출력 범위는 0~1사이
• 입력값이 크면 1에 가까워지고 작을수록 0에 가까움

  식

  $[ f(x) = \frac{1}{1 + e^{-x}} ]$

def sigmoid(x): # S자 형태 그래프, 미분이 가능 
    y = 1.0/(1.0 + np.exp(-x))
    return y
# 시그모이드 그래프 시각화 
y = sigmoid(x)
plt.plot(x,y)
plt.plot([0,0], [1.0, 0.0], ':')
plt.title('sigmoid 그래프')
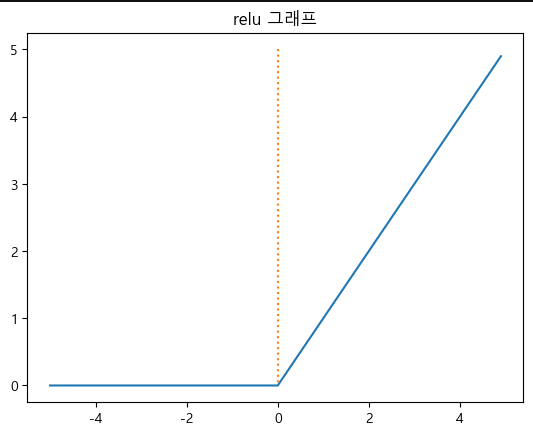
plt.show()

렐루 함수 (ReLU: Rectified Linear Unit)

• 입력값이 0보다 크면 그대로 출력, 0이하면 0으로 출력하는 함수
• 비선형 활성화 함수
• 계산이 간단하고 빠름
• 대부분의 은닉층에서 기본값으로 사용

  식

  $[ f(x) = \begin{cases} x, & \text{if } x > 0 \\ 0, & \text{otherwise} \end{cases} ]$

def relu(x):
    return np.maximum(x,0)
# Relu 그래프 시각화
y = relu(x)
plt.plot(x,y)
plt.plot([0,0], [5.0, 0.0], ':')
plt.title('relu 그래프')
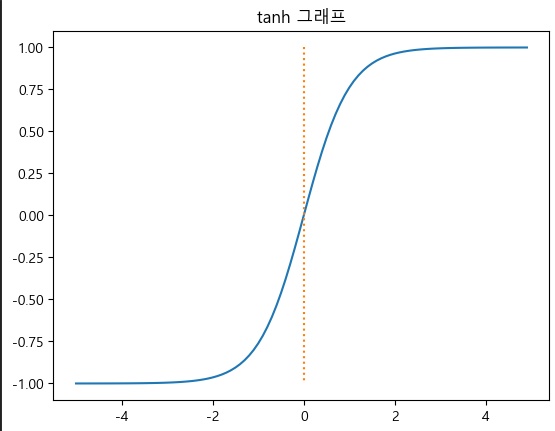
plt.show()

하이퍼볼릭 탄젠트 함수 (Tanh Function)

• 시그모이드 함수처럼 S자 형태이지만 -1에서 1사이의 출력 범위를 가짐
• 시그모이드보다 학습 안정적 -> 중심이 0

def tanh(x):
    return np.tanh(x)
# tanh 그래프 시각화 
y = tanh(x)
plt.plot(x,y)
plt.plot([0,0], [1.0, -1.0], ':')
plt.title('tanh 그래프')
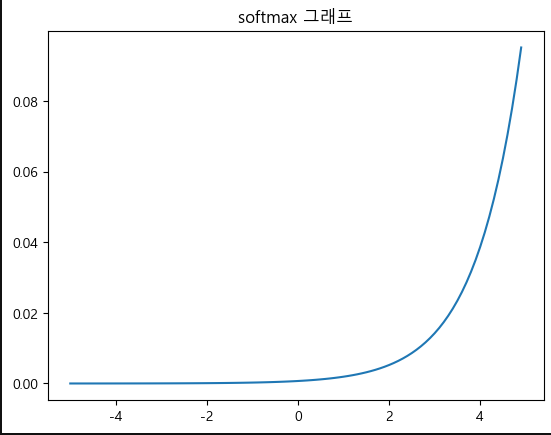
plt.show()

소프트맥스 함수 (Softmax Function)

• 입력값들을 지수 함수로 변환뒤, 각 값의 비율을 출력
• 각 글래스에 대한 확률 분포 출력
• 한 클래스에 높은 확률, 나머지에는 낮은 확률을 부여하는 경향이 있음
• 다중 클래스 분류의 출력층에서 사용

def softmax(x):
    y = np.exp(x)/np.sum(np.exp(x))
    return y
#softmax 그래프 시각화 
y = softmax(x)
plt.plot(x,y)
plt.title('softmax 그래프')
plt.show()