[iOS 2주차] Swift: 시간복잡도와 공간복잡도

// ChatGPT 4o prompt:
Swift에서 시간복잡도와 공간복잡도에 대해서 설명해줘

시간복잡도와 공간복잡도

시간복잡도와 공간복잡도는 알고리즘의 효율성을 측정하는 중요한 개념이다.

1. 시간복잡도 (Time Complexity)

• 정의: 시간복잡도는 알고리즘이 실행되는 데 걸리는 시간을 입력 크기 ( n )에 대한 함수로 표현한 것이다. 입력의 크기가 커질수록 알고리즘이 얼마나 더 오래 걸리는지를 보여준다.
• 표기법: 일반적으로 빅오 표기법 ( O )을 사용해 최악의 경우 실행 시간을 나타낸다.
• 예시:
  • 상수 시간 ( O(1) ): 입력 크기와 상관없이 실행 시간이 일정한 경우 (예: 배열의 첫 번째 요소 접근).
  • 선형 시간 ( O(n) ): 입력 크기에 비례하여 실행 시간이 증가하는 경우 (예: 배열 전체 탐색).
  • 로그 시간 ( O(\log n) ): 입력 크기가 증가해도 실행 시간이 비교적 느리게 증가하는 경우 (예: 이진 탐색).
  • 제곱 시간 ( O(n^2) ): 중첩 루프를 사용하는 경우 (예: 이중 for문).

2. 공간복잡도 (Space Complexity)

• 정의: 공간복잡도는 알고리즘이 실행되는 동안 필요한 메모리 양을 입력 크기( n )에 대한 함수로 나타낸 것이다. 알고리즘이 실행되면서 얼마나 많은 메모리를 추가로 사용하는지를 보여준다.
• 표기법: 마찬가지로 빅오 표기법을 사용하여 표현한다.
• 예시:
  • 상수 공간 ( O(1) ): 알고리즘이 입력 크기에 상관없이 일정한 메모리 공간을 사용하는 경우.
  • 선형 공간 ( O(n) ): 입력 크기에 비례하여 메모리 사용량이 증가하는 경우 (예: 새로운 배열을 생성하여 입력 데이터를 저장할 때).
  • 이차 공간 ( O(n^2) ): 2차원 배열이나 행렬을 다룰 때.

이러한 복잡도 분석을 통해 알고리즘이 입력 크기에 따라 실행 시간과 메모리 사용량이 어떻게 변하는지 이해할 수 있으며, 효율적인 알고리즘을 설계하는 데 도움을 준다. Swift에서도 표준 라이브러리의 여러 메서드와 알고리즘에 대해 시간 및 공간복잡도를 고려하여 최적화할 수 있다.

// ChatGPT 4o prompt:
꼭 Swift에 해당되는 얘기가 아닌거네?

시간복잡도와 공간복잡도는 특정 프로그래밍 언어에 국한되지 않고, 알고리즘 전반에 걸쳐 적용되는 개념이다. Swift에서도 동일한 개념을 적용하여 코드의 효율성을 분석할 수 있지만, 이러한 복잡도는 Swift뿐만 아니라 Python, Java, C++ 등 모든 언어에 적용된다.

다만, Swift에 특화된 예를 들면, Swift의 Array나 Dictionary 같은 자료 구조에 대해서도 시간복잡도를 설명할 수 있다:

• Swift의 Array:

  • 요소 접근: O(1)
  • 요소 추가 (끝에): O(1) (가끔 재할당 시 O(n) )
  • 요소 삽입/삭제 (중간): O(n)

• Swift의 Dictionary:

  • 요소 삽입/삭제: O(1) (평균적인 경우)
  • 요소 탐색: O(1) (평균적인 경우)

이러한 복잡도를 이해하면 Swift에서 어떤 자료 구조나 메서드를 선택할 때 성능을 최적화하는 데 큰 도움이 된다.

// ChatGPT 4o prompt:
O는 왜 O인거야?

빅오 표기법의 "O"는 수학 용어인 "Order"에서 유래한 것이다. 이 표기법은 "어떤 함수의 성장이 다른 함수에 비해 얼마나 빠르게 증가하는지를 나타내는 정도(order)"를 표현하기 위해 사용된다.

더 자세한 설명:

• 빅오 표기법의 목적: 알고리즘의 시간이나 공간 복잡도를 설명할 때, 입력 크기 ( n )이 커질수록 실행 시간이나 메모리 사용량이 어떻게 변하는지 표현하기 위해 사용된다.
• 왜 O를 사용하는가?: "Order of growth"라는 표현에서 'Order'를 따와서 사용한다. 예를 들어, 알고리즘이 ( O(n) )이라면 이는 해당 알고리즘이 선형적으로 증가하는 성장을 나타낸다는 의미이다.

이처럼 빅오 표기법은 단순히 "성장률의 차수(order)"를 나타내는 기호이며, 다른 복잡도 표기법인 Ω(빅오메가)나 Θ(빅세타)도 각기 다른 의미를 가지면서 비슷한 맥락에서 사용된다.

// ChatGPT 4o prompt:
다른 복잡도 표기법이 있어? 코드를 최적화하는데 유용한 표기법이라면 알려줘.

복잡도 표기법

빅오 표기법 외에도 알고리즘의 성능을 설명할 때 사용되는 몇 가지 다른 복잡도 표기법이 있다. 각각은 특정 시나리오에서 알고리즘의 효율성을 더 정확하게 나타낼 수 있다. 코드를 최적화할 때 유용할 수 있는 주요 표기법은 다음과 같다:

1. 빅오 표기법 (Big O, O)

• 용도: 최악의 경우의 실행 시간이나 공간을 나타낸다.
• 예: 알고리즘이 최악의 상황에서 얼마나 느려질 수 있는지를 측정한다.
• 사용: 대부분의 경우 빅오 표기법을 사용해 최악의 성능을 기준으로 알고리즘을 비교한다.

2. 빅오메가 표기법 (Big Omega, Ω)

• 용도: 알고리즘의 최상의 경우 실행 시간이나 공간을 나타낸다.
• 예: 알고리즘이 최적의 상황에서 얼마나 빠르게 작동할 수 있는지를 보여준다.
• 사용: 알고리즘이 얼마나 빠를 수 있는지를 평가할 때 사용된다. 최적화가 가능한 부분을 이해하는 데 도움이 된다.

3. 빅세타 표기법 (Big Theta, Θ)

• 용도: 알고리즘의 실행 시간이나 공간이 최상과 최악의 경우가 동일한 경우를 나타낸다.
• 예: 알고리즘이 항상 일정한 성능을 가진다면 Θ로 표기된다.
• 사용: 알고리즘이 입력에 따라 일정하게 실행되며 시간 복잡도의 변동이 없는 경우를 명확히 설명할 때 유용하다.

예시를 통해 살펴보기:

배열에서 특정 요소를 찾는 알고리즘을 가정해보면:

• 빅오 표기법 ( O(n) ): 최악의 경우 요소가 배열의 끝에 있거나 존재하지 않는 경우, 전체 배열을 탐색해야 함.
• 빅오메가 표기법 ( Ωa(1) ): 최상의 경우 요소가 배열의 첫 번째 위치에 있어 한 번만 탐색하면 됨.
• 빅세타 표기법 ( Θ(n) ): 최악과 최상의 경우가 동일할 때, 즉 항상 배열 전체를 탐색해야 할 때 사용.

최적화에 어떻게 유용한가?

• 빅오 표기법을 사용해 최악의 경우를 고려하여 알고리즘의 성능을 보수적으로 평가하고, 성능 저하가 발생할 수 있는 시나리오를 분석할 수 있다.
• 빅오메가 표기법은 최적화의 잠재력을 파악하는 데 도움을 주며, 빅세타 표기법은 알고리즘이 특정 성능을 항상 보장할 수 있는지를 판단하는 데 유용하다.

이 세 가지 표기법을 함께 이해하면 알고리즘을 다양한 시나리오에서 평가하고 최적화할 수 있는 기준을 세우는 데 도움이 된다.

// ChatGPT 4o prompt:
자료구조나 메서드를 보고 어느정도 복잡도를 파악하고 싶은데, 어떤 개념들을 익혀야 가능할까?

복잡도 파악을 위한 개념들

1. 기본적인 자료구조의 이해

자료구조마다 기본적인 연산의 시간복잡도와 공간복잡도가 다르다. 대표적인 자료구조와 그 복잡도를 파악하면 알고리즘을 분석할 때 유리하다.

• 배열 (Array): 요소 접근 ( O(1) ), 삽입/삭제 ( O(n) - 중간 위치).
• 연결 리스트 (Linked List): 요소 접근 ( O(n) ), 삽입/삭제 ( O(1) - 특정 위치에서)
• 스택과 큐: 삽입과 삭제가 모두 ( O(1) ) (끝에서만 이루어질 때).
• 해시맵/딕셔너리 (HashMap/Dictionary): 삽입, 삭제, 탐색이 보통 ( O(1) ) (평균적인 경우).
• 이진 탐색 트리 (Binary Search Tree): 탐색, 삽입, 삭제가 평균 ( O(log n) ) (최악의 경우 O(n) ).
• 힙 (Heap): 삽입과 삭제가 ( O(log n) ).

2. 알고리즘의 시간복잡도 분석 방법

• 반복문: 중첩된 반복문일수록 복잡도가 증가한다. 예를 들어, 단일 루프는 ( O(n) ), 이중 중첩 루프는 ( O(n^2) ).
• 재귀: 재귀 호출은 시간복잡도를 분석하기 어려울 수 있다. 재귀 함수의 호출 횟수를 추적하고, 호출당 수행되는 작업을 이해하는 것이 중요하다.
• 분할정복: 알고리즘이 문제를 절반으로 나눠가며 해결할 때는 보통 ( O(log n) ) 또는 ( O(n log n) )의 시간복잡도를 가진다 (예: 병합 정렬).

3. 빅오 표기법의 기본 및 심화 개념

• ( O(1) ): 상수 시간.
• ( O(log n) ): 로그 시간 (예: 이진 탐색).
• ( O(n) ): 선형 시간.
• ( O(n log n) ): 선형 로그 시간 (예: 효율적인 정렬 알고리즘).
• ( O(n^2) ): 이차 시간 (예: 버블 정렬).
• ( O(2^n) ), ( O(n!) ): 지수 및 팩토리얼 시간 (예: 일부 재귀적 문제).

4. 공간복잡도 분석

알고리즘이 사용하는 메모리 공간을 이해하는 것도 중요하다.

• 알고리즘이 추가적인 데이터 구조를 얼마나 많이 사용하는지, 재귀 호출이 스택 메모리를 어떻게 사용하는지 등을 파악해야 한다.
• ( O(1) ) 공간복잡도는 알고리즘이 일정한 메모리를 사용한다는 의미이다.
• ( O(n) ) 공간복잡도는 입력 크기에 비례한 메모리를 사용한다는 의미이다.

5. 데이터 접근 및 변경 패턴 이해

• 랜덤 접근 vs. 순차 접근: 자료구조에 따라 요소에 접근하거나 변경할 때 걸리는 시간이 달라진다.
• 변경 및 삽입/삭제: 특정 자료구조에서의 삽입/삭제가 효율적인지(예: 배열 vs. 연결 리스트).

6. 알고리즘 설계 패턴

알고리즘 설계에 사용되는 일반적인 패턴을 익히면 복잡도를 예상하기 쉽다.

• 투 포인터: 배열이나 리스트를 순차적으로 탐색할 때 사용되며, 대부분 ( O(n) ) 복잡도이다.
• 슬라이딩 윈도우: ( O(n) ) 시간복잡도로 연속된 부분을 처리하는 데 사용된다.
• 분할정복: ( O(log n) ) 또는 ( O(n log n) )로 문제를 분할해 해결한다.
• 동적 프로그래밍: 중복된 계산을 줄이고 시간복잡도를 ( O(n) ) 또는 ( O(n^2) )로 줄이는 기법이다.

이 개념들을 숙지하고 각 자료구조와 알고리즘이 작동하는 방식을 이해하면, 자료구조나 메서드의 시간복잡도와 공간복잡도를 더 쉽게 파악할 수 있다.

ChatGPT 4o with canvas prompt:
뭐 어떤 게 효율적인 복잡도인지 감이 잘 안 오는데, 그래프로 그려서 보여줄 수 있어?

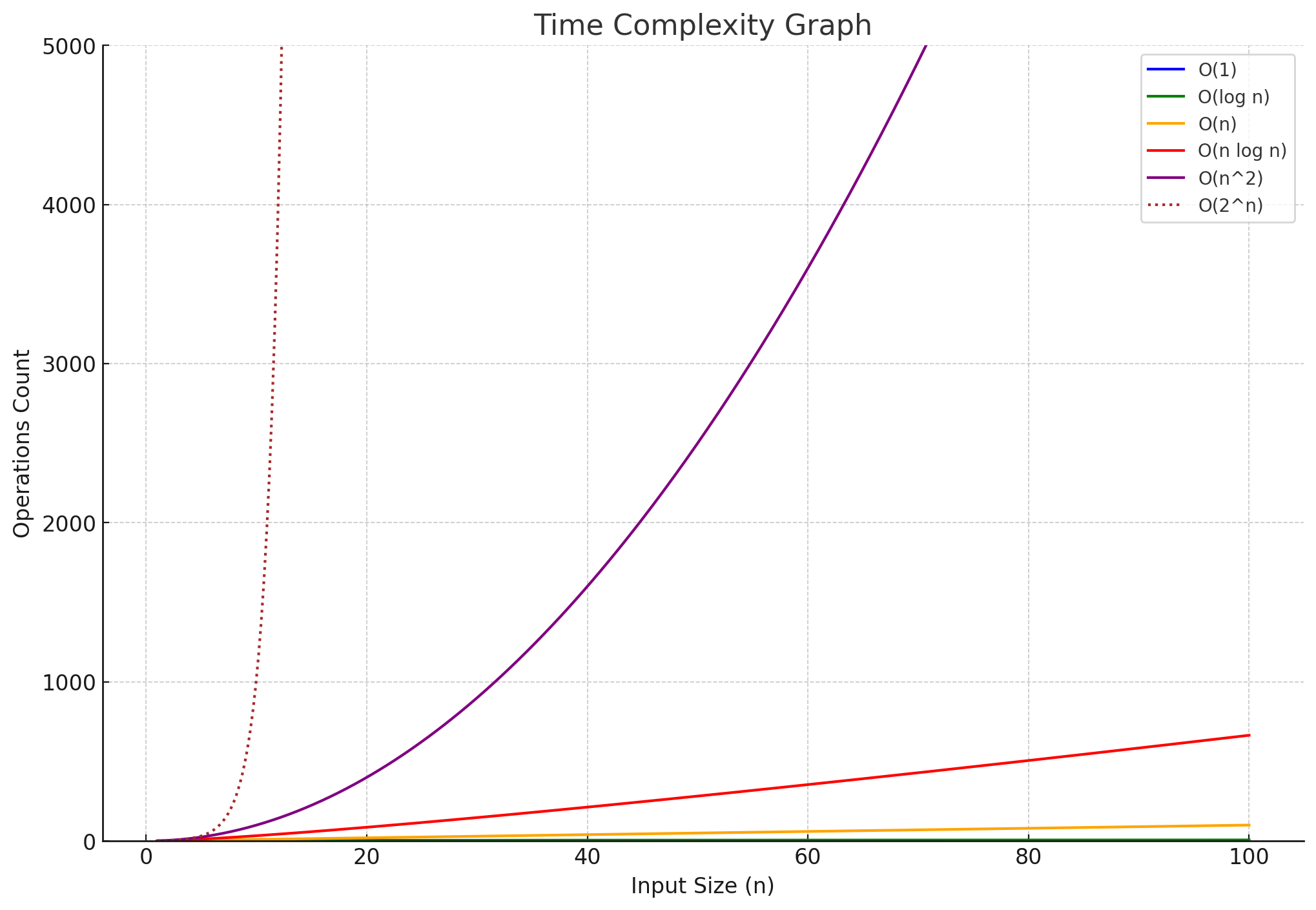
시간복잡도 그래프

시간복잡도 그래프 ( 입력 크기: n )

위 그래프는 다양한 시간복잡도의 성장률을 시각적으로 비교한 것이다. 각 복잡도는 다음과 같은 의미를 가진다:

1. O(1) 상수 시간: 입력 크기에 상관없이 일정한 시간만 걸린다. 매우 효율적이다.
2. O(\log n) 로그 시간: 입력 크기가 증가해도 시간의 증가가 완만하다. 이진 탐색 같은 알고리즘에 해당한다.
3. O(n) 선형 시간: 입력 크기에 비례해 시간이 증가한다. 전체 요소를 한 번씩 순회할 때 해당한다.
4. O(n \log n) 선형 로그 시간: ( O(n) )과 ( O(\log n) )이 결합된 형태로, 병합 정렬 같은 효율적인 정렬 알고리즘이 이에 해당한다.
5. O(n^2) 이차 시간: 입력이 커질수록 시간이 급격히 증가한다. 버블 정렬, 삽입 정렬 등 중첩 루프를 사용하는 알고리즘에서 자주 나타난다.
6. O(2^n) 지수 시간: 입력 크기가 커질수록 매우 빠르게 시간이 증가한다. 보통 비효율적이며, 해결 가능한 크기에 제한이 있다.

효율적인 알고리즘은 가능한 한 O(\log n) 또는O(n)에 가깝도록 설계하는 것이 좋다.