[iOS 7주차] Algorithm: 이중우선순위큐 2부 - Min-Max Heap

DoyleHWorks·2024년 12월 6일
algorithm공부
1

내일배움캠프-iOS-5기-본캠프

목록 보기
45/64

문제: 힙 - 이중우선순위큐

힙 문제 목록 링크 / 문제 링크 / Github 링크
import Foundation

func solution(_ operations:[String]) -> [Int] {
    return []
}

※ 이전 글에서 이어짐

문제 접근 2

  • 이중 우선순위 큐 구현 옵션
    1. 두 개의 힙 사용 (Min-Heap + Max-Heap) ❌
    2. Min-Max Heap 사용 ✅
    3. Balanced Binary Search Tree (균형 이진 탐색 트리)
import Foundation

// Min-Max Heap 구조체 정의
struct MinMaxHeap<T: Comparable> {
    // 힙 요소를 저장하는 배열
    var elements: Array<T> = []
    
    // 힙의 최소값 (Min-Max Heap에서 항상 루트 노드에 위치)
    var minimum: T? {
        guard !elements.isEmpty else { return nil }
        return elements[0]
    }
    
    // 힙의 최대값 (Min-Max Heap에서 루트의 두 자식 중 큰 값)
    var maximum: T? {
        guard !elements.isEmpty else { return nil }
        if elements.count == 1 {
            return elements[0] // 힙에 하나만 있으면 최소값과 최대값이 동일
        } else if elements.count == 2 {
            return elements[1] // 루트의 하나의 자식만 있는 경우
        } else {
            return max(elements[1], elements[2]) // 두 자식 중 더 큰 값 반환
        }
    }
    
    // 최대값 제거
    mutating func removeMax() -> T? {
        guard !elements.isEmpty else { return nil }
        
        if elements.count == 1 {
            return elements.removeLast() // 하나만 남은 경우 바로 제거
        } else if elements.count == 2 {
            return elements.removeLast() // 두 개만 있는 경우 루트의 자식 제거
        } else {
            let maxIndex = elements[1] > elements[2] ? 1 : 2 // 최대값의 인덱스
            let maxValue = elements[maxIndex]
            elements[maxIndex] = elements.removeLast() // 최대값을 마지막 원소로 대체
            bubbleDown(from: maxIndex) // Max-level의 규칙 복구
            return maxValue
        }
    }
    
    // 최소값 제거
    mutating func removeMin() -> T? {
        guard !elements.isEmpty else { return nil }
        let minValue = elements[0] // 루트에 있는 최소값 저장
        
        if elements.count == 1 {
            elements.removeLast() // 하나만 남은 경우 바로 제거
        } else {
            elements[0] = elements.removeLast() // 마지막 원소로 루트를 대체
            bubbleDown(from: 0) // Min-level의 규칙 복구
        }
        return minValue
    }
    
    // 새 값 삽입
    mutating func insert(_ value: T) {
        elements.append(value) // 힙의 맨 끝에 삽입
        bubbleUp(from: elements.count - 1) // 적절한 위치로 이동하며 Min-Max Heap 규칙 유지
    }
    
    // 삽입 시 값의 위치를 올바르게 조정
    private mutating func bubbleUp(from index: Int) {
        let currentIndex = index
        let parentIndex = self.parentIndex(index)
        
        if isMinLevel(currentIndex) { // 현재 노드가 Min-level인 경우
            if elements[parentIndex] < elements[currentIndex] { // 부모가 더 작으면 Max-level 규칙 위반
                elements.swapAt(parentIndex, currentIndex)
                bubbleUpMax(from: parentIndex) // Max-level로 버블 업
            } else {
                bubbleUpMin(from: currentIndex) // Min-level로 버블 업
            }
        } else { // 현재 노드가 Max-level인 경우
            if elements[parentIndex] > elements[currentIndex] { // 부모가 더 크면 Min-level 규칙 위반
                elements.swapAt(parentIndex, currentIndex)
                bubbleUpMin(from: parentIndex) // Min-level로 버블 업
            } else {
                bubbleUpMax(from: currentIndex) // Max-level로 버블 업
            }
        }
    }
    
    // Min-level에서 버블 업 (조부모와 비교하며 이동)
    private mutating func bubbleUpMin(from index: Int) {
        var currentIndex = index
        while let grandparentIndex = self.grandparentIndex(currentIndex), elements[currentIndex] < elements[grandparentIndex] {
            elements.swapAt(grandparentIndex, currentIndex)
            currentIndex = grandparentIndex
        }
    }
    
    // Max-level에서 버블 업 (조부모와 비교하며 이동)
    private mutating func bubbleUpMax(from index: Int) {
        var currentIndex = index
        while let grandparentIndex = self.grandparentIndex(currentIndex), elements[currentIndex] > elements[grandparentIndex] {
            elements.swapAt(grandparentIndex, currentIndex)
            currentIndex = grandparentIndex
        }
    }
    
    // 버블 다운 (값을 적절히 이동시켜 Min-Max Heap 규칙 유지)
    private mutating func bubbleDown(from index: Int) {
        if isMinLevel(index) {
            bubbleDownMin(from: index)
        } else {
            bubbleDownMax(from: index)
        }
    }
    
    // Min-level에서 버블 다운
    private mutating func bubbleDownMin(from index: Int) {
        guard let smallestIndex = findSmallestCandidateIndex(from: index) else { return }
        
        if elements[index] > elements[smallestIndex] {
            if isGrandChildIndex(smallestIndex, of: index) { // 손자와 교환
                elements.swapAt(index, smallestIndex)
                let parentIndex = self.parentIndex(smallestIndex)
                if elements[smallestIndex] < elements[parentIndex] { // 부모와의 규칙도 확인
                    elements.swapAt(smallestIndex, parentIndex)
                }
                bubbleDownMin(from: smallestIndex)
            } else { // 자식과 교환
                elements.swapAt(index, smallestIndex)
            }
        }
    }
    
    // Max-level에서 버블 다운
    private mutating func bubbleDownMax(from index: Int) {
        guard let largestIndex = findLargestCandidateIndex(from: index) else { return }
        
        if elements[index] < elements[largestIndex] {
            if isGrandChildIndex(largestIndex, of: index) { // 손자와 교환
                elements.swapAt(index, largestIndex)
                let parentIndex = self.parentIndex(largestIndex)
                if elements[largestIndex] < elements[parentIndex] { // 부모와의 규칙도 확인
                    elements.swapAt(largestIndex, parentIndex)
                }
                bubbleDownMax(from: largestIndex)
            } else { // 자식과 교환
                elements.swapAt(index, largestIndex)
            }
        }
    }
    
    // 현재 노드가 Min-level인지 확인
    private func isMinLevel(_ index: Int) -> Bool {
        Int(log2(Double(index + 1))) % 2 == 0
    }
    
    // 부모 노드의 인덱스 계산
    private func parentIndex(_ index: Int) -> Int {
        ( index - 1 ) / 2
    }
    
    // 조부모 노드의 인덱스 계산
    private func grandparentIndex(_ index: Int) -> Int? {
        guard index > 2 else { return nil }
        return parentIndex(parentIndex(index))
    }
    
    // 왼쪽 자식 노드의 인덱스 계산
    private func leftChildIndex(_ index: Int) -> Int {
        index * 2 + 1
    }
    
    // 오른쪽 자식 노드의 인덱스 계산
    private func rightChildIndex(_ index: Int) -> Int {
        index * 2 + 2
    }
    
    // Min-level에서 가장 작은 후보 인덱스 찾기
    private func findSmallestCandidateIndex(from index: Int) -> Int? {
        let indices = [leftChildIndex(index), rightChildIndex(index),
                       leftChildIndex(leftChildIndex(index)), rightChildIndex(leftChildIndex(index)),
                       leftChildIndex(rightChildIndex(index)), rightChildIndex(rightChildIndex(index))]
        return indices.filter { $0 < elements.count }.min(by: { elements[$0] < elements[$1] })
    }

    // Max-level에서 가장 큰 후보 인덱스 찾기
    private func findLargestCandidateIndex(from index: Int) -> Int? {
        let indices = [leftChildIndex(index), rightChildIndex(index),
                       leftChildIndex(leftChildIndex(index)), rightChildIndex(leftChildIndex(index)),
                       leftChildIndex(rightChildIndex(index)), rightChildIndex(rightChildIndex(index))]
        return indices.filter { $0 < elements.count }.max(by: { elements[$0] < elements[$1] })
    }
    
    // 특정 노드가 손자인지 확인
    private func isGrandChildIndex(_ childIndex: Int, of parentIndex: Int) -> Bool {
        let leftChildIndex = self.leftChildIndex(parentIndex)
        let rightChildIndex = self.rightChildIndex(parentIndex)
        
        return childIndex == self.leftChildIndex(leftChildIndex) || childIndex == self.rightChildIndex(leftChildIndex) || childIndex == self.leftChildIndex(rightChildIndex) || childIndex == self.rightChildIndex(rightChildIndex)
    }
}
  • solution 함수 구현
    • I 숫자 : 큐에 주어진 숫자를 삽입합니다.
    • D 1 : 큐에서 최댓값을 삭제합니다.
    • D -1 : 큐에서 최솟값을 삭제합니다.
    • 큐가 비어있으면 [0,0], 비어있지 않으면 [최댓값, 최솟값]을 반환
    • 큐가 비어있으면 삭제 연산 무시
    • 최댓값/최솟값 연산의 대상이 둘 이상인 경우 하나만 삭제
func solution(_ operations:[String]) -> [Int] {
    var heap = MinMaxHeap<Int>()
    
    for operation in operations {
        let commands = operation.components(separatedBy: " ")
        let behaviour = commands[0]
        guard let value = Int(commands[1]) else { continue }
        
        if behaviour == "I" {
            heap.insert(value)
        } else {
            if value == 1 {
                _ = heap.removeMax()
            } else {
                _ = heap.removeMin()
            }
        }
    }
    
    let maxValue = heap.maximum ?? 0
    let minValue = heap.minimum ?? 0
    
    return [maxValue, minValue]
}
테스트 통과 실패

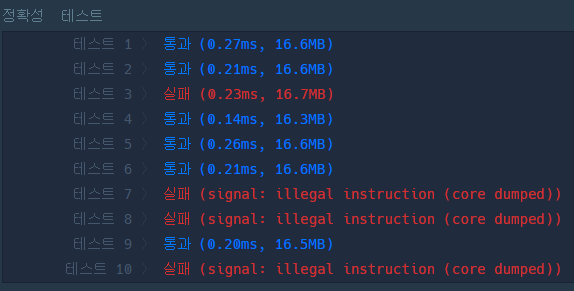디버깅 시도

func solution(_ operations:[String]) -> [Int] {
    var heap = MinMaxHeap<Int>()
    
    print("") // 디버깅 print
    
    for operation in operations {
        let commands = operation.components(separatedBy: " ")
        guard commands.count == 2, let value = Int(commands[1]) else { continue }
        
        let behaviour = commands[0]
        if behaviour == "I" {
            heap.insert(value)
        } else if behaviour == "D" {
            if value == 1 {
                _ = heap.removeMax()
            } else if value == -1 {
                _ = heap.removeMin()
            }
        }
        
        print("[\(operation)] \(heap.elements)") // 디버깅 print
    }
    
    let maxValue = heap.maximum ?? 0
    let minValue = heap.minimum ?? 0
    
    // 비어 있는 경우 [0, 0] 반환
    return heap.elements.isEmpty ? [0, 0] : [maxValue, minValue]
}
print 동작 안함

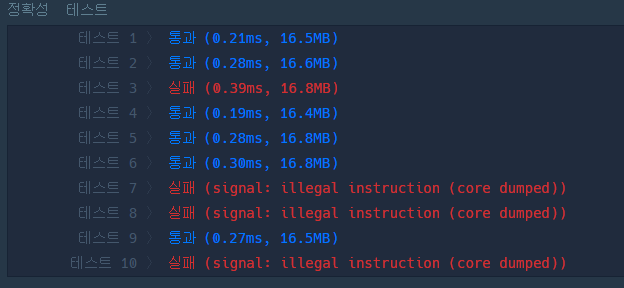문제 접근 3

그냥 sort 쓰기

import Foundation

struct MinMaxHeap {
    private var elements: [Int] = []
    
    var isEmpty: Bool {
        return elements.isEmpty
    }
    
    var max: Int? {
        return elements.max()
    }
    
    var min: Int? {
        return elements.min()
    }
    
    mutating func insert(_ value: Int) {
        elements.append(value)
        elements.sort()
    }
    
    mutating func deleteMax() {
        if let maxIndex = elements.indices.max(by: { elements[$0] < elements[$1] }) {
            elements.remove(at: maxIndex)
        }
    }
    
    mutating func deleteMin() {
        if let minIndex = elements.indices.min(by: { elements[$0] < elements[$1] }) {
            elements.remove(at: minIndex)
        }
    }
}

// Solution Function
func solution(_ operations: [String]) -> [Int] {
    var heap = MinMaxHeap()
    
    for operation in operations {
        let components = operation.split(separator: " ")
        let command = components[0]
        let value = Int(components[1])!
        
        if command == "I" {
            heap.insert(value)
        } else if command == "D" {
            if value == 1 {
                heap.deleteMax()
            } else if value == -1 {
                heap.deleteMin()
            }
        }
    }
    
    if heap.isEmpty {
        return [0, 0]
    } else {
        return [heap.max ?? 0, heap.min ?? 0]
    }
}
테스트 통과



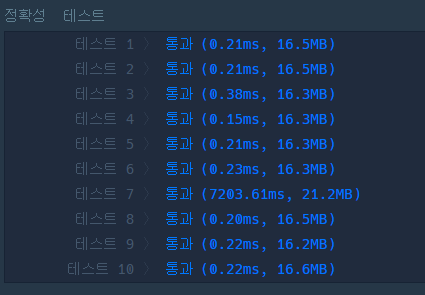???: 바보 같은 놈, 네 녀석이 아무리 기어도 sort() 하나에 정리되는 것을..
네가 이진트리를 붙잡으며 낭비한 시간을 땅을 치며 후회하도록 해라.

What I've learned:

bubbleUp의 원리

주어진 원소 A에 대하여,

  1. 새로운 원소 A를 힙의 맨 뒤에 추가한다.
  2. A가 위치한 레벨이 Min-level인지 Max-level인지 판단한다.
    • 추가된 원소가 트리의 깊이(레벨)를 기준으로 Min-level인지 Max-level인지 결정된다.
    • (깊이가 짝수면 Min-level, 홀수면 Max-level.)
  3. A를 부모와 비교한다:
    • A가 Max-level이고 A가 부모보다 작다면, A와 부모를 교환한다.
    • A가 Min-level이고 A가 부모보다 크다면, A와 부모를 교환한다.
  4. A를 조부모와 비교한다:
    • A가 Min-level이고 A가 조부모보다 작다면, A와 조부모를 교환한다.
    • A가 Max-level이고 A가 조부모보다 크다면, A와 조부모를 교환한다.
  5. 부모 또는 조부모와 교환이 이루어졌다면, A의 새로운 위치에서 3번 과정을 반복한다.
  6. 교환이 더 이상 필요하지 않을 경우, 알고리즘을 종료한다.

bubbleDown의 원리

주어진 원소 A에 대하여,

  1. 만약 A가 Min-level이라면:
  • A의 자식들과 손자들 중 가장 작은 값을 가진 원소를 B라고 하고 B의 인덱스를 i라고 한다.
  • B가 A보다 더 작은 값을 가지고 있다면:
    • 만약 B가 A의 손자라면:
      • B와 A의 위치를 서로 바꾼다.
      • A가 새로운 위치에서 부모보다 더 큰 값을 가지게 되었다면, A와 부모의 위치를 바꾼다.
      • i번째 위치에서 Bubble Down 알고리즘을 재귀적으로 다시 수행한다.
    • 만약 B가 A의 자식이라면:
      • B와 A의 위치를 바꾸고 알고리즘을 종료한다(자식 레벨만 점검해도 규칙이 복구됨).
  1. 만약 A가 Max-level이라면:
  • A의 자식들과 손자들 중 가장 큰 값을 가진 원소를 B라고 하고 B의 인덱스를 i라고 한다.
  • B가 A보다 더 큰 값을 가지고 있다면:
    • 만약 B가 A의 손자라면:
      • B와 A의 위치를 서로 바꾼다.
      • A가 새로운 위치에서 부모보다 더 작은 값을 가지게 되었다면, A와 부모의 위치를 바꾼다.
      • i번째 위치에서 Bubble Down 알고리즘을 재귀적으로 다시 수행한다.
    • 만약 B가 A의 자식이라면:
      • B와 A의 위치를 바꾸고 알고리즘을 종료한다(자식 레벨만 점검해도 규칙이 복구됨).

본문의 내용과 관계는 없지만, 오늘 ChatGPT와 대화했던 내용:
https://chatgpt.com/share/6753032e-b580-8008-aea7-e456ecc67107

profile
DoyleHWorks
Reciprocity lies in knowing enough
이전 포스트

[iOS 7주차] Array vs Linked List, Amortized Analysis, etc.

다음 포스트

[iOS 8주차] Project PokeContact: MVVM-C 아키텍처 도입

0개의 댓글