[자료구조] 해시 테이블 -해시 충돌-

최예닮·2023년 1월 3일

해시테이블에 대해 계속해서 이야기 해보겠다.

해시의 충돌

해시 테이블은 충돌 문제가 발생할 수 있습니다. 그림을 우선 살펴보자

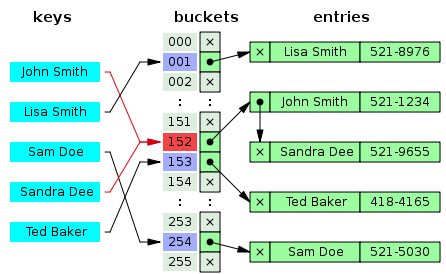
위 그림을 살펴보면 해시 함수를 통해 152 라는 인덱스를 배정받고 Smith 와 Dee 가 충돌되고 있는걸 볼 수 있다. 이렇게 같은 인덱스를 배정 받으면 어떻게 처리해주면 좋을까?

개방 주소법 (Open Address)

해시 충돌이 발생하면 테이블 내의 새로운 주소를 탐사하여 비어있는 곳에 충돌된 데이터를 입력하는 방식이 있다. 개방 주소법은 어떤 방식으로 비어있는 공간을 탐사할 것이냐에 따라 나누어진다. 한번 살펴보도록하자

1. 선형 탐사법

선형 탐사법은 순차적으로 탐사하는 방법이다. 우선 코드를 통해 충돌 상황을 만들어보자

function hashFunction (key) {
  return key % 10;
}

console.log(hashFunction(1001)); // 1
console.log(hashFunction(11)); // 1

위 두 해시는 인덱스로 1이 나올 것이다. 그렇기때문에 충돌이 발생을하는데 선형 탐사법은 이렇게 충돌이 났을 때 정해진 칸만큼의 옆 방을 주는 방법이다.

이렇게 저장하게 되는데 만약에 인덱스가 또 1 이 나온다면 충돌이 발생하겠죠 ? 그럼 또 값을 3번에 저장할 것이다. 이런 방식으로 빈 공간이 나타날 때까지 순차적으로 탐사를 진행한다.

선형 탐사법의 단점은 특정 해시 값의 주변이 모두 채워져 있는 일차 군집화(Primary Clustering) 문제에 취약하다는 것입니다.

선형 탐사법을 사용하면 연속되게 저장될 가능성이 높아진다. 만약에 2, 3 가 나오게 되면 이미 1 에서 충돌해서 빈 공간에 저장한 친구들과 또 충돌이 나게 되는 것이다.
이런식으로 충돌이 되면 데이터가 연속되게 저장되기 때문에 데이터 덩어리가 커지게 된다. 이것이 일차 군집화 라고 한다. 그럼 다른 방법을 살펴보자.

2. 제곱 탐사법

제곱 탐사법은 탐사하는 폭이 고정이 아니고 제곱으로 늘어난다.
예시로 첫번째 충돌이 발생했을 때 충돌 난 지점으로부터 1의 제곱만큼 두번째는 2의 제곱만큼 세번째는 3의 제곱만큼 스탭이 커진다.

위 방법은 선형 탐사법보다 데이터의 밀집도가 낮기 때문에 연쇄적으로 충돌이 발생할 확률이 많이 줄어든다.
하지만 1이 여러번 나오게 되면 충돌이 나는 것을 피할 수 없다. 결국에는 데이터의 군집은 피할 수 없는 숙명 이다. 이 현상을 이차 군집화 라고 부른다.

3. 이중 해싱

이중 해싱은 말그대로 해시 함수를 이중으로 사용하는 것을 뜻한다.
하나는 최초 해시를 얻을 때 사용하고, 다른 하나는 충돌이 났을 경우 탐사 이동폭을 얻기 위해 사용한다. 이렇게 하면, 최초 해시로 같은 값이 나오더라도 다른 해시 함수를 거치면서 다른 탐사 이동폭을 제공하기 때문에 다른 공간에 값이 골고루 저장될 확률이 높아진다.

const myTableSize = 23; // 테이블 사이즈가 소수여야 효과가 좋다
const myHashTable = [];

const getSaveHash = value => value % myTableSize;

// 스텝 해시에 사용되는 수는 테이블 사이즈보다 약간 작은 소수를 사용한다.
const getStepHash = value => 17 - (value % 17);

const setValue = value => {
  let index = getSaveHash(value);
  let targetValue = myHashTable[index];
  while (true) {
    if (!targetValue) {
      myHashTable[index] = value;
      console.log(`${index}번 인덱스에 ${value} 저장! `);
      return;
    }
    else if (myHashTable.length >= myTableSize) {
      console.log('풀방입니다');
      return;
    }
    else {
      console.log(`${index}번 인덱스에 ${value} 저장하려다 충돌 발생!ㅜㅜ`);
      index += getStepHash(value);
      index = index > myTableSize ? index - myTableSize : index;
      targetValue = myHashTable[index];
    }
  }
}

이때 테이블 사이즈와 두 번째 해시함수에 사용될 수는 둘 다 소수를 사용하는 것이 좋다. 둘 중에 하나가 소수가 아니라면 결국 언젠가 같은 해싱이 반복되기 때문!

1. 저장할 인덱스를 getSaveHash 해시 함수로 얻습니다.
2. myHashTable에 index를 키로 받는 값을 targetValue 변수에 저장합니다.
3. 반복문을 시작합니다.
4. 만약 targetValue가 없으면, 배열에 값이 비었다는 뜻이므로, 인덱스에 맞는 키값을 저장합니다. 
5. 만약 배열의 길이가 myTableSize의 길이보다 크거나 같다면 배열이 모두 꽉 찼다는 뜻입니다.
6. 만약 인덱스에 맞는 키값이 있고, 배열이 가득 차 있지도 않다면 인덱스에 맞는 키값을 저장하려다가 충돌이 발생합니다.
그렇다면 다음 인덱스를 받아서, 그 인덱스에 맞는 값으로 키값을 저장합니다.

console.log(setValue(1001)); 
console.log(setValue(11)); 
console.log(setValue(21)); 
console.log(setValue(31)); 

// 12번 인덱스에 1001 저장! 
// 11번 인덱스에 11 저장! 
// 21번 인덱스에 21 저장! 
// 8번 인덱스에 31 저장!