저는 Resnet에 대한 개념을 2015년에 최초로 발표한 논문을 리뷰해보도록 하겠습니다. 논문의 흐름대로 분석해보았습니다.
0. Abstract
기존 이미지 분류 모델들(CNN, VGGNet 등)의 문제점은 모델이 깊어질수록 학습시키기 어렵다는 점이었다. 이 논문에서는 이 문제점을 해결하기 위해서 residual learning framework를 고안했다. 이 논문에서 말하는 Residual learning이란 layer의 input을 참조하여 residual function(잔차 함수)를 학습하는 것을 말한다.
1. Introduction
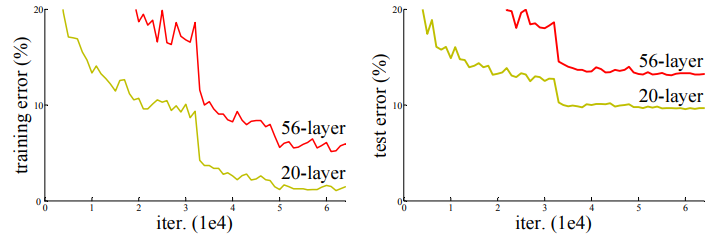
사진을 보면, layer가 깊은 모델일수록 training error와 test error 모두 높은 것을 확인할 수 있다. (이는 원인이 overfitting만이 아니라는 것을 보여준다.)
이 논문에서는 결정적인 원인을 gradient vanishing/exploding이라고 설명하고 있다.
더 깊은 네트워크에 대한 연구가 진행될수록, degradation 문제가 대두되었다. Network depth가 증가하고, accuracy는 빠르게 저하되었다. 그리고 이 논문에서는 이런 문제를 해결하는 것에 있어서 기존과 비슷한 방법으로는 해결하기 어렵다고 판단했다.
그래서 shallower architecture를 사용해 deeper architecture를 만드는 것을 시도했다. Identity mapping으로 shallower architecture를 기존 모델에 추가하였다. 이 아이디어는 shallower 모델을 추가한 deeper 모델의 training error가 shallower 모델의 training error 보다 높을 수 없다는 아이디어에서 시작했다.
(쉽게 말해서, 최소한 shallower 모델의 성능은 보장할 것이라는 아이디어)
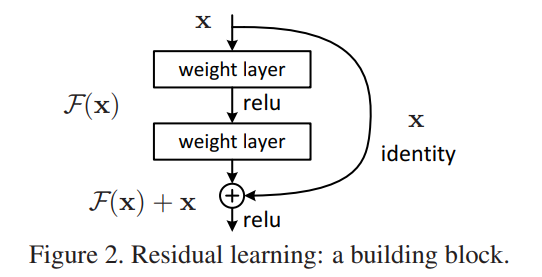
이 사진이 이 논문에서 degradation problem을 해결하기 위해 고안해낸 deep residual learning framework이다.
쌓여진 레이어가 그 다음 레이어에 바로 적합되는 것이 아니라 residual mapping에 적합하도록 만들었다. 기존의 mapping을 H(x)라고 표기하고, layer를 또 다른 mapping인 F(x) = H(x) - x에 학습하도록 하였다. Original mapping은 F(x) + x 가 되는 것이다.
이 논문에서는 original mapping을 최적화하는 것보다 resiual mapping을 최적화하는 것이 더 쉽다고 가정했다. 만약 identity mapping이 H(x)에 최적화가 될수록, 결국 residual function(F)가 0에 가장 가까운 최소값으로 수렴하게 될 것이다.
추가적으로 좀 더 설명해보면, 이 논문에서는 identity mapping(x)와 H(x)의 초기값이 근사하다는 것을 실험을 통해 증명했다고 하고 있다. 이 것은 residual function(F)는 초기값부터 크기가 굉장히 작은 값이고 (F = H - x 이기 때문에), 그렇다는 것은 기존의 모델보다 값의 변화폭이 적고, 그렇기 때문에 학습에 더 용이하다고 말하고있다.
Shortcut connections
이 논문에서는 x라는 identity mapping을 shortcut connection으로 추가하였다. shortcut connection은 1개 혹은 그 이상의 layer를 skip하게 된다. 그리고 최종적으론 기존의 stacked layer의 output과 이 shortcut connection의 output이 더해지게 된다.
이는 굉장히 큰 이점이 있다고 설명하고 있는데, 첫번째는 다른 parameter와 computational complexity를 증가시키지 않는 점이고, 두번째는 기존 곱셈연산에서 덧셈연산으로 바뀐다는 점이다.
첫번째 이점은 연산에 있어서 x라는 덧셈 하나만 추가되기 때문이다.
두번째 이점은 back propagation 과정에서 큰 의미를 가지는데, 기존에는 모델이 깊어짐에 따라 back propagation 과정에서 기울기가 소실되거나 발산하는 경우가 많았다. 그런데 x라는 identity mapping이 더해지면서 미분 과정에 최소한 상수값이 무조건 남게 되면서 매우 깊은 모델의 back propagation 과정에서 굉장히 큰 이점을 가질 수 있었다.
2. Deep Residual Learning
2.1. Residual Learning
H(x)를 기본 mapping이라고 간주하고, x가 input일 때, 다수의 비선형 레이어가 복잡한 함수를 점근적으로 근사 할 수 있다고 가정하면 잔차함수, 즉 H(x) - x를 저절로 근사 할 수 있다.
(굉장히 당연한 말인데, 기존의 목표가 x를 H(x)에 근사하는 것이라면, H(x) - x도 당연히 근사할 수 있음.)
수학적으로 봤을 땐 H(x) = F(x) + x와 H(x) - x = F(x)는 다름이 없지만, 형태에 따라 학습의 용이함이 달라진다.
위에서도 설명했듯이, H(x)를 그대로 학습하는 것 보다 F(x)라는 잔차함수를 학습하는 것이 더 쉽다. 상대적으로 값의 변화폭이 적고, 값의 크기 자체도 상대적으로 작기 때문에.
2.2. Identity Mapping by Shortcuts
이 논문에서는 residual learning을 모든 layer에 적용했다. 그리고!
building block을 다음과 같이 정의했다.

x: input
y: output
F: residual mapping
W: weight
이 F + x operation은 shortcut connection을 통해 이루어진다. 이 shortcut connection은 더 많은 parameter나 computation complexity를 증가시키지 않는다. 이 부분은 학습 뿐만 아니라 plain 과 residual network 사이의 comparison에서도 중요하다.
Residual Network는 short connection으로 인해 Plain Network에 비해 같은 깊이, 너비, 파라미터 수를 가지면서도 더 효과적으로 학습할 수 있다. Degradation problem을 해결하기 위해 단순한 네트워크 구조에서 residual connection을 추가하는 것 만으로도 더 나은 성능을 기대할 수 있다.

입력 x와 F(x)의 차원이 다를 경우, 차원을 맞추기 위해 linear projection을 사용할 수 있다. Ws라는 가중치 행렬을 곱해 차원을 맞춰준다. 그러나 실험 결과, 대부분의 경우에선 identity mapping(Ws없이 그냥 x를 더하는 것)만으로 충분하며, Ws는 차원이 다를 때만 사용한다.
2.3. Network Architecture

- Plain Network
baseline 모델로 사용한 plain net은 VGGNet에서 영감을 얻었다. 즉, conv filter의 사이즈가 3*3이고 다음 2가지 규칙에 기반하여 설계하였다.
A. Output feature map의 size가 같은 layer들은 모두 같은 수의 conv filter를 사용한다.
B. Output feature map의 size가 반으로 줄어들면 time complexity를 동일하게 유지하기 위해 필터 수를 2배로 늘려준다.Downsampling을 수행할 땐 stride가 2인 filter를 사용했다. Network의 끝엔 global average pooling layer와 Softmax와 함께 1000-way fully-connected layer를 사용했다. 결과적으로 전체 layer의 수는 34이다.
- Residual Network
Plain 모델에 기반하여 Shortcut connection을 추가하여 구성한다. 이 때, input과 output의 차원이 같다면, identity shortcut을 바로 사용하면 되지만, dimension이 증가했을 경우 두가지 선택지가 있다.
1. zero padding을 적용하여 차원을 키워준다.
2. 앞서 다뤘던 projection shortcut을 사용한다. (1X1 convolution/Ws)이 때, shortcut이 feature map을 2 size씩 건너뛰므로 stride를 2로 설정한다.
2.4. Implementation
단순한 구현 방법을 설명한다.
1. 짧은 쪽이 [256, 480] 사이가 되도록 random 하게 resize 수행
2. horizontal flip 부분적으로 적용 및 per-pixel mean을 빼준다
3. 224 x 224 사이즈로 random 하게 crop 수행
4. standard color augmentation 적용
5. z에 Batch Normalization 적용
6. He 초기화 방법으로 가중치 초기화
7. Optimizer : SGD (mini-batch size : 256)
8. Learning rate : 0.1에서 시작 (학습이 정체될 때 10씩 나눠준다)
9. Weight decay : 0.0001
10. Momentum : 0.9
11. 60 X 10^4 반복 수행
12. dropout 미사용
3. Experiments
plain 모델의 깊이에 따른 error 비교
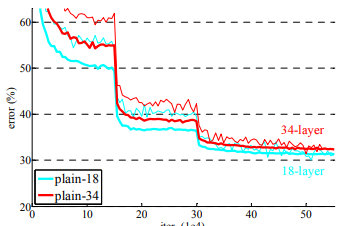
먼저 plain 모델에 대해 실험을 수행하였는데, 더 깊은 plain 모델에서 더 높은 validation error가 나타났다. training, validation error 모두 비교해본 결과, 34 layer plain 모델에서 training error도 높았기 때문에 degradation 문제가 있다고 판단했다.
Resnet 모델의 깊이에 따른 error 비교

다음으로, ResNet 모델을 plain 모델과 비교해보았다. 이때, 모든 Shortcut은 identity mapping을 사용하고, 차원을 키우기 위해 zero padding을 사용하였기에 파라미터 수는 증가하지 않았다.
실험 결과, 다음 3가지를 확인할 수 있었다.
-
더 깊은 34-ResNet 모델이 19-ResNet 모델보다 2.8% 가량 높은 성능을 보였다. training, validation error 모두 상당히 낮은 것을 볼 수 있었고, 이는 degradation 문제가 잘 해결되었고 depth가 증가하더라도 좋은 정확도를 유지할 수 있다는 것을 보여주었다.
-
이 표를 보면 알 수 있듯이 layer의 수가 늘어날 수록 error가 줄어드는 것을 볼 수 있고, 이는 residual learning이 extremely deep system에서 매우 효과적임을 알 수 있다.

- 18-layer의 plain net과 ResNet을 비교했을 때 성능은 거의 유사했지만, 수렴 속도에서 차이가 있었다. 과도하게 모델이 깊지 않은 경우, 같은 상황에서 ResNet이 plain net보다 더 빨리 수렴할 수 있다.
Identity VS Projection Shortcuts
위에서 얘기했듯이 x와 F의 차원을 맞춰주는 방법은 두가지가 있는데, 첫번째 방법이 zero padding을 이용하는 것이고, 두번째 방법이 linear projection을 이용해서 맞춰주는 것이다. 이 부분에선 이 방법들을 사용해서 성능을 비교해볼려고 한다. 다음 3가지 옵션에 대해 비교하였다.
A. zero padding을 사용한 경우 (dimension을 맞춰줄 때만 사용)
B. projection shorcut을 사용한 경우 (dimension을 키워줄 때만 사용)
C. 모든 shortcut으로 projection shorcut을 사용한 경우
3가지 옵션 모두 plain 모델보단 좋은 성능을 보였고, 그 순위는 A<B<C였다. 하지만 그 성능차가 미미하였기 때문에 projection shortcut이 degradation 문제를 해결하는데 필수적이진 않다는 것을 확인할 수 있었다.
Bottleneck Architectures

실험을 진행할 때 학습 시간이 너무 길어질 것 같아 구조를 bottleneck architecture로 바꿨다. 따라서 F는 3-layer stack 구조로 바뀌게 되고, 이는 1x1, 3x3, 1x1 conv로 구성된다. 1x1은 dimension을 줄였다가 늘리는 역할을 한다.
(위에 그림에서 64-d에서 256-d으로 늘어난 이유는 identity mapping을 위해 차원을 맞춰주기 위해 zero padding을 적용한 것으로 보임.)
50-layer ResNet
34-layer ResNet의 2-layer block을 3-layer bottleneck block으로 대체하여 50-layer ResNet을 구성하였다. 이 때, 차원을 맞춰주기 위해서 B 옵션을 사용하였다.
101-layer and 152-layer ResNet
더 많은 3-layer bottleneck block을 사용하여 101-layer와 152-layer ResNet을 구성하였다. Depth가 굉장히 증가하였음에도 VGG-16/19 모델보다 낮은 complexity를 보여줬다. Degradation 문제도 없이 상당히 높은 정확성을 보여줬다.
기존 모델들과 성능 비교
 기존 모델들과 비교해봐도 ResNet이 훨씬 더 좋은 성능을 보여주고 있다.
기존 모델들과 비교해봐도 ResNet이 훨씬 더 좋은 성능을 보여주고 있다.
Analysis of Layer Responses
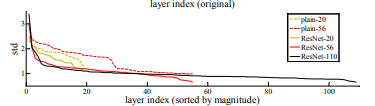
이 사진은 위에서 말했던 residual function이 non-residual function보다 일반적으로 0에 가까울 것이라는 주장을 뒷받침해준다. Depth가 깊어질수록 response가 감소하는 것은 ResNet이 depth가 깊어질수록 signal이 감소하는 경향이 있다는 것을 보여준다.
