그리디(Greedy) 알고리즘

허준기·2025년 1월 6일

알고리즘

목록 보기

5/6

그리디(Greedy) 알고리즘

뜻 그대로 탐욕적인 알고리즘 
다음 상황을 고려하지 않고 당장의 순산에 있는 최적의 상황만을 찾아 해답에 도달하는 방식
순간마다 하는 선택은 지역적으로는 최적이지만, 그 선택들이 모였을때 항상 최적이라는 보장은 없다

조건

최적 부분 구조 : 지역적으로 최적이면서 전역적으로 최적인 문제들에 적용
→ 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성

탐욕적 선택 속성 : 앞의 선택이 이후의 선택에 영향을 주지 않을 경우

위의 2가지 조건을 만족하지 못하는 경우 그리디 알고리즘은 최적해를 구하지 못함
최적해를 구하지 못하더라도, 근사 알고리즘으로 사용할 수 있음 → 계산 속도가 빨라서 실용적

풀 수 있는 문제

거스름돈 문제

어떤 물건을 사고 거스름돈을 줄 때 가장 작은 동전의 수로 제공하는 경우

500, 100, 50, 10원 동전이 있을때 1460원에 대한 거스름돈의 동전 개수

1460 - 500 = 960
960 - 500 = 460
460 - 100 = 360
360 - 100 = 260
260 - 100 = 160
160 - 100 = 60
60 - 50 = 10
10 - 10 = 0

가장 적은 동전의 수를 가진 거스름돈을 제공하려면, 가장 높은 금액을 가진 동전을 많이 주면 된다

위의 순서로 거스름돈을 제공한다면,
500 - 2개
100 - 4개
50 - 1개
10 - 1개

총 8개로 가장 적은 동전의 개수로 거스름돈을 줄 수 있다

풀 수 없는 문제

트리 구조에서 가장 큰 합을 구하는 경우

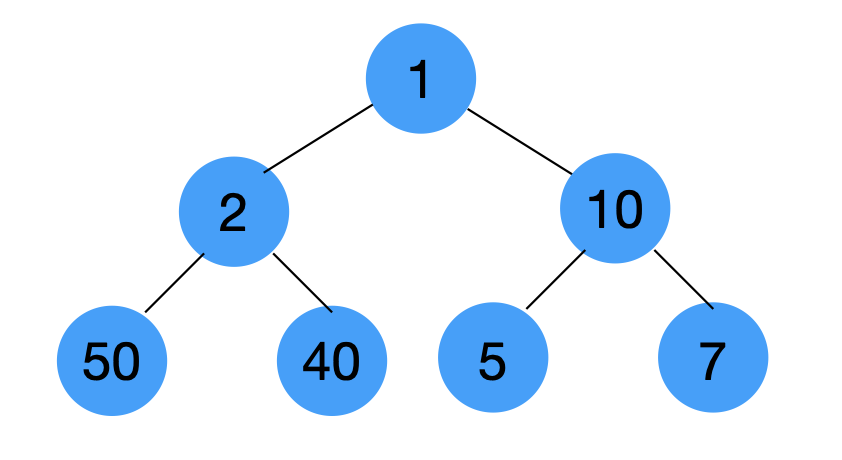
이렇게 생긴 트리가 있다고 가정해보자

그리디 알고리즘을 사용해서 최대의 합을 구해본다면
1 → 10 → 7 로 최댓값이 18이 나온다

하지만 위의 트리구조에서의 최댓값은
1 → 2 → 50 으로 53이다

예시로 든 트리구조의 경우 그리디 알고리즘의 조건인 탐욕적 선택 속성에 맞지 않는다

매트로이드

그리디 알고리즘이 최적해를 가려낼 수 있는지를 판별하게 해주는 수학적 공간

탐욕적 방법을 적용할 수 있는 모든 경우를 판별해낼 수 있는 것은 아님

문제풀이 백준 1439

문제

다솜이는 0과 1로만 이루어진 문자열 S를 가지고 있다. 
다솜이는 이 문자열 S에 있는 모든 숫자를 전부 같게 만들려고 한다. 
다솜이가 할 수 있는 행동은 S에서 연속된 하나 이상의 숫자를 잡고 모두 뒤집는 것이다. 
뒤집는 것은 1을 0으로, 0을 1로 바꾸는 것을 의미한다.

예를 들어 S=0001100 일 때,
전체를 뒤집으면 1110011이 된다.
4번째 문자부터 5번째 문자까지 뒤집으면 1111111이 되어서 2번 만에 모두 같은 숫자로 만들 수 있다.
하지만, 처음부터 4번째 문자부터 5번째 문자까지 문자를 뒤집으면 한 번에 0000000이 되어서 1번 만에 모두 같은 숫자로 만들 수 있다.

문자열 S가 주어졌을 때, 다솜이가 해야하는 행동의 최소 횟수를 출력하시오.

입력

첫째 줄에 문자열 S가 주어진다. S의 길이는 100만보다 작다.

출력

첫째 줄에 다솜이가 해야하는 행동의 최소 횟수를 출력한다.

문제를 보고 든 생각은 0으로 이루어진 문자열의 개수와 1로 이루어진 문자열의 개수를 구한 다음에 비교하면 된다고 생각했다!

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String S = br.readLine();

        int zeroCount = 0;
        int oneCount = 0;
        int i = 0;

        while (i < S.length()) {
            char currentChar = S.charAt(i);

            while (i < S.length() && S.charAt(i) == currentChar) {
                i++;
            }

            if (currentChar == '0') {
                zeroCount++;
            }

            if (currentChar == '1') {
                oneCount++;
            }
        }

        System.out.println(Math.min(zeroCount, oneCount));
    }
}