이번주의 알고리즘은 다익스트라(Dijkstra) 이다

다익스트라 알고리즘

DP를 활용한 최단 경로 탐색 알고리즘
하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려줌 → 음수로 된 간선은 X - 음수가 없기 때문에 현실에서 사용하기 적합

DP인 이유는 최단거리가 여러개의 최단 거리로 이루어져 있기 때문!
도착할 정점 뿐만 아니라 모든 다른 정점까지 최단 경로로 방문해서 각 정점까지 최단 경로를 찾음

과정

1. 출발 노드와 도착 노드 정하기
2. 최단 거리 테이블 조회
3. 현재 노드와 근처 노드 중 방문하지 않은 노드를 찾고, 방문하지 않은 노드 중 거리가 가장 짧은 노드 선택 → 해당 노드 방문 처리
4. 그 노드를 거쳐서 다른 노드로 넘어가는 가중치를 계산해서 최단 거리 테이블 업데이트

내가 이해한 바로는 최단 거리 테이블에 계속해서 찾게 된 최단거리를 업데이트 하고 그 중에서 가장 짧은 거리를 반환하면 될것 같다

문제를 풀면서 이해해보자!

백준 5972 - 택배 배송

택배 배송 문제

문제

현서는 찬홍이에게 택배를 배달
가는 길에 만나는 소들에게 여물을 줘야함 - 최소한의 소들을 만나면서 가고싶음

입력

N: 헛간
M: 길의 개수
A: 떨어진 헛간 1
B: 떨어진 헛간 2
C: 길에 있는 소의 마리

흠... 어렵다

아무리 봐도 문제가 풀리지 않아 결국 다른 블로그 봤다...
코드를 보고 어떤식으로 진행되는지 이해를 해봐야지...

package baekjun.dijkstra;

import java.io.*;
import java.util.*;

public class P5972 {
    public static int N, M;
    public static List<List<Node>> graph = new ArrayList<>();
    public static boolean[] visited;
    public static int[] d = new int[50001];

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        N = Integer.parseInt(st.nextToken());   // 헛간 개수
        M = Integer.parseInt(st.nextToken());   // 길 개수

        visited = new boolean[N];               // 방문 여부

        for(int i=0;i<=N;i++) {
            graph.add(new ArrayList<>());
        }

        for(int i=0;i<M;i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken()); // 시작 헛간
            int b = Integer.parseInt(st.nextToken()); // 끝 헛간
            int dist = Integer.parseInt(st.nextToken()); // 비용

            // 양방향 간선
            graph.get(a).add(new Node(b, dist)); // a 에서 b 까지의 거리
            graph.get(b).add(new Node(a, dist)); // b 에서 a 까지의 거리
        }

        dijkstra(1); // 다익스트라 진행

        System.out.println(d[N]);	// 최종 결과
    }

    public static void dijkstra(int start) {
        Arrays.fill(d, Integer.MAX_VALUE); // 처음에는 무한대(정수형 최대)로 채워줌

        PriorityQueue<Node> pq = new PriorityQueue<>();
        pq.offer(new Node(start, 0)); // 제자리 거리는 0
        d[start] = 0; // 시작노드에서 시작노드까지의 가중치는 제자리 이므로 0

        while (!pq.isEmpty()) {
            Node temp = pq.poll();  // 가장 가까운 노드
            int nodeB = temp.nodeB; // 현재 노드번호
            int distance = temp.distance; // 현재 노드까지 거리

            if(d[nodeB] < distance) continue; // 현재 노드가 이미 처리된적이 있는 노드라면 무시 ( 거리가 더 작다는것은 이미 더 효율적인 방안으로 처리된 것 )

            for(int i=0;i<graph.get(nodeB).size();i++) { // 현재 노드와 연결된 다른 헛간
                int cost = d[nodeB] + graph.get(nodeB).get(i).distance; // cost = 현재노드의 가중치 + 현재노드와 다음 노드까지의 간선의 가중치

                if( cost < d[graph.get(nodeB).get(i).nodeB]) { // 새롭게 측정한 비용이 다음 노드가 원래 가지고 있던 가중치보다 적을 경우
                    d[graph.get(nodeB).get(i).nodeB] = cost; // 더 적은 값으로 갱신해준다
                    pq.offer(new Node( graph.get(nodeB).get(i).nodeB, cost)); // 계속 탐색을 해봐야 모든 노드들의 최솟값을 알 수 있기 때문에 현재의 가중치를 가지고 계속 탐색
                }
            }
        }
    }
}

class Node implements Comparable<Node>{
    int nodeB; //목적지 헛간
    int distance; // 시작노드에서 nodeB 까지의 거리
    public Node(int nodeB, int distance) {
        this.nodeB = nodeB;
        this.distance = distance;
    }

    @Override
    public int compareTo(Node other) {
        if(this.distance > other.distance) {
            return 1;
        }else if(this.distance == other.distance) {
            return 0;
        }else {
            return -1;
        }
    }
}

주석이 달려있긴 하지만 하나씩 살펴보자

main 에 있는 부분은 거의 입력을 받는 부분이라 패스
dijkstra 함수 부분을 살펴보자

우선순위 큐 를 사용하는 것을 볼 수 있다

들어가는 순서와 상관없이 우선순위가 높은 데이터가 먼저 나가는 큐

우선순위 큐를 이용해서 가장 가까운 거리에 있는 헛간부터 방문하는 방식이다

코드에 대한 설명은 주석에 달려있다 - 출처

문제에 있는 예시로 어떻게 동작하는지 한번 살펴보자

입력

6 8
4 5 3
2 4 0
4 1 4
2 1 1
5 6 1
3 6 2
3 2 6
3 4 4

입력은 이렇게 들어오고 이를 그림으로 그리면

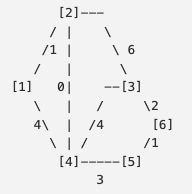
이렇게 생겼다
1번 헛간에서 출발해서 6번 헛간까지 가는 과정이다

출발 헛간	1	2	3	4	5	6
초기 상태	0	∞	∞	∞	∞	∞
1번 헛간	0	1	∞	4	∞	∞
2번 헛간	0	1	7	1	∞	∞
4번 헛간	0	1	5	1	4	∞
5번 헛간	0	1	5	1	4	5
3번 헛간	0	1	5	1	4	5

표로 그려보면 이렇다
일단 초기 상태는 1번 헛간에서 출발하니 제자리는 0이고 나머지는 아직 몰라서 ∞ 로 표현해줬다

이제 출발을 해보자!

문제 과정

1. 1번 헛간에서 갈 수 있는곳은 2번과 4번이다 해당 거리는 1과 4 그대로 입력을 해주면 된다 → 비교할게 없음

2. 그 다음에 우선순위 큐를 이용해 가장 가까운 2번 헛간에서 갈 수 있는 곳을 알아본다. 2번에서 갈 수 있는 곳은 3번과 4번이다. 우선 3번으로 가는 것은 기존 값이 없으니 1번에서 2번까지의 거리 1과 2번에서 3번까지의 거리 6을 더해 7을 넣어준다. 그리고 2번에서 4번까지의 거리가 0인데 1 + 0 = 1 을 통해서 1번에서 4번까지의 거리가 1로 업데이트 되는 것을 알 수 있다!!

3. 그 다음으로 가까워진 4번 헛간에서 출발해서 위의 행위를 동일하게 해준다. 4번에서 갈 수 있는 곳은 3번과 5번이다. 1 -> 4 -> 3을 통해 3번까지의 최소 거리가 5로 업데이트 된다. 그리고 5번까지의 거리는 기존에 아무것도 없었으므로 1 + 3 인 4를 업데이트 시킨다

4. 그 다음 우선순위인 5번과 3번 헛간에 대해서 반복해 주면 최종 목적지인 6번까지의 최소 거리가 5인 것을 볼 수 있다

후기

다익스트라 개념만 공부했을 때는 이런식으로 해야할 지 모르고 그냥 이중 배열과 값을 저장할 테이블 하나만 있으면 될 줄 알았는데 Node나 우선순위 큐 같은 다른 것들도 이용해야 했다. 물론 다른 방법이 있겠지만 그건 계속 공부해야겠다..
지금은 개념을 익힌다는 느낌으로 한문제씩 풀고 있는데 추후에는 각 알고리즘 별로 이해할때까지 푸는 시간이 필요할 것 같다