TIL 2020-12-15 (N-QUEENS)

nyongho·2020년 12월 18일
N Queens
0

JavaScript

목록 보기
17/23
post-thumbnail

4. Algorithm

TIL List

  • DFS,BFS
  • BACK TRACKING
  • 나의 알고리즘 사고의 단계
  • N-QUEENS

1) DFS

Depth First Search, 한국어 표기는 깊이 우선 탐색.
트리나 그래프에서 한 루트로 탐색하다가 특정 상황에서 최대한 깊숙히 들어가서 확인한 뒤 다시 돌아가 다른 루트로 탐색하는 방식이다. 대표적으로 백트래킹에 사용한다. 일반적으로 재귀호출을 사용하여 구현하지만, 단순한 스택 배열로 구현하기도 한다.

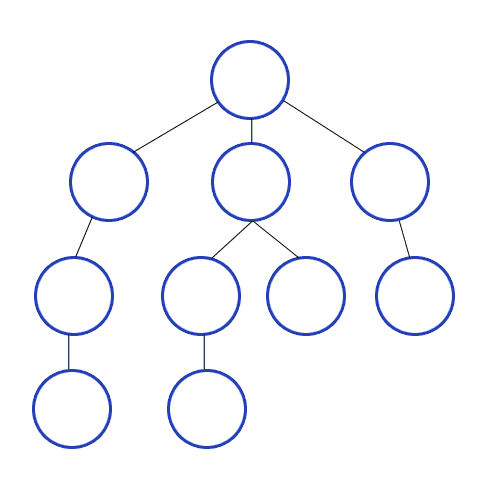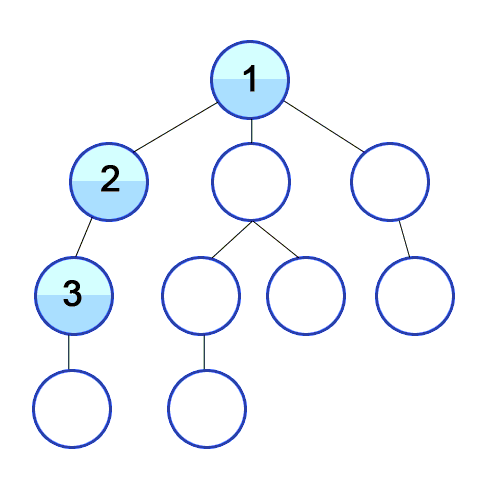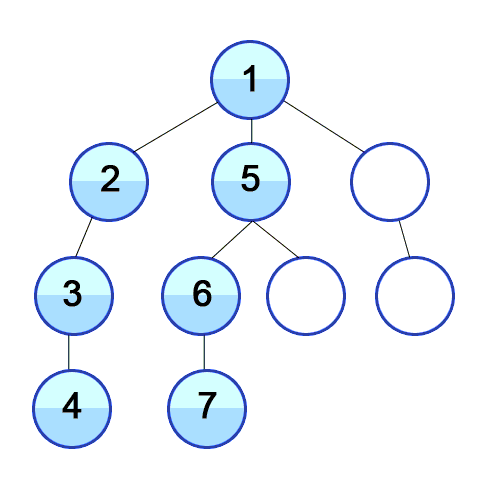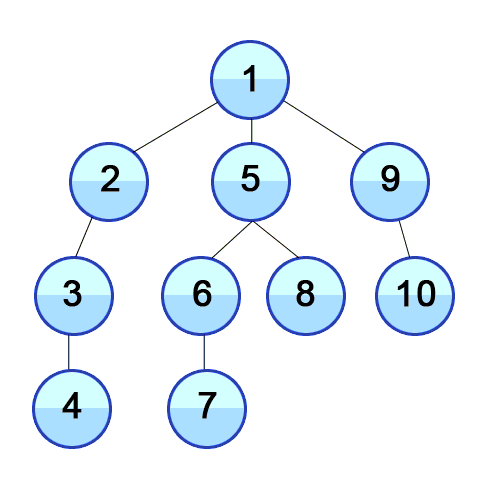
(자식의 자식을 파고들고 모두 파고 들었으면 부모로 다시 돌아간다)

DFS는 상태공간을 나타낸 트리에서 바닥에 도달할 때까지 한 쪽 방향으로만 내려가는 방식이다. 미로찾기를 생각하면 쉽다. 한 방향으로 들어갔다가 막다른 길에 다다르면(=트리의 바닥에 도착) 왔던 길을 돌아가서 다른 방향으로 간다. 이 짓을 목표지점(=원하는 해)이 나올 때까지 반복한다.

2) BFS

Breadth First Search, 한국어 표기는 넓이 우선 탐색.
탐색 알고리즘 중 DFS와 비교되는 방법으로, 가장 가까운 곳들을 먼저 탐색하고, 그 다음 거리에 있는 것들을 탐색하는 방법이다.

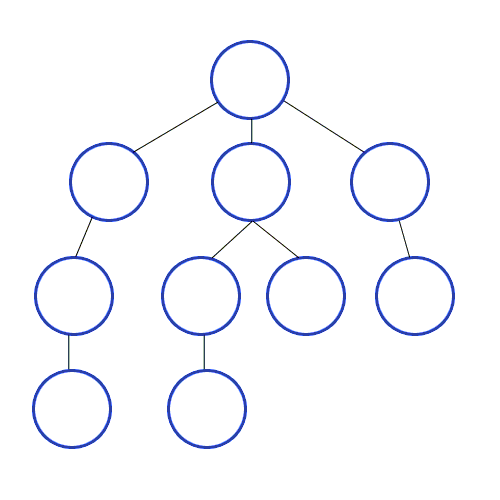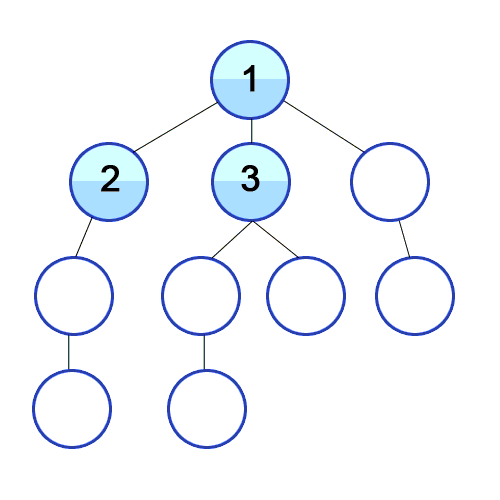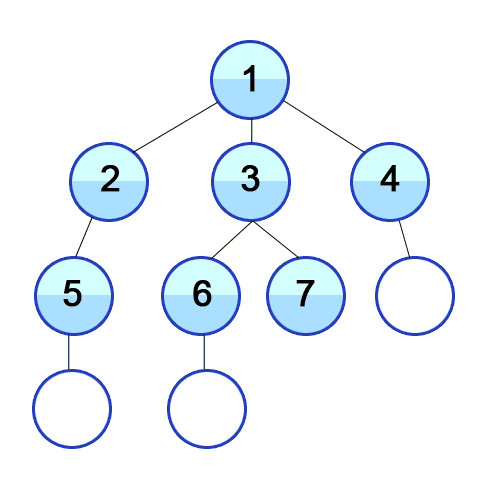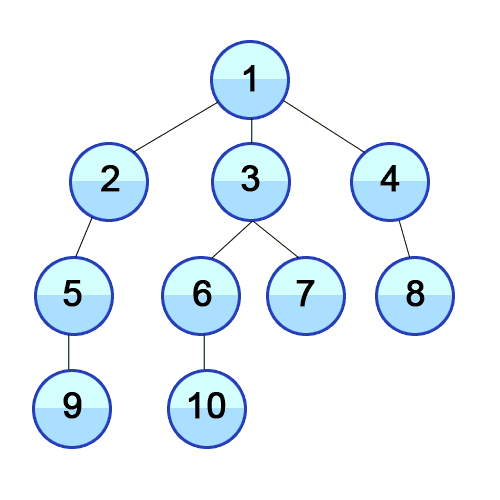
(레벨 단위로 탐색하는 모습)

BFS는 모든 분기점을 다 검사하면서 진행하는 방식이다. 철수와 영희가 계단에서 가위바위보를 하고 있을 때, "철수가 원하는 지점에 갈 수 있는 최소 승리 횟수는 얼마인가?" 같은 문제에서 효과를 발휘한다. 이 경우 DFS는 깊이가 무한인 경우에 빠져나오지 못하며, 중복 방지를 한다고 치더라도 올바른 해를 찾는데 시간이 많이 걸린다. BFS는 모든 분기를 다 검색하면서 상태공간을 탐색한다. 철수가 이겼을 때, 비겼을 때, 졌을 때를 검사하고, 그 경우마다 각각 또 다른 3가지 가능성을 전부 검사한다. 이러다가 어느 한 부분에서 원하는 해를 발견하면, 이것이 최단 거리가 된다.

3) BACK TRACKING

모든 경우의 수를 전부 고려하는 알고리즘. 상태공간을 트리로 나타낼 수 있을 때 적합한 방식이다. 일종의 트리 탐색 알고리즘이라고 봐도 된다. 방식에 따라서 깊이 우선 탐색(Depth First Search, DFS)과 너비 우선 탐색(Breadth First Search, BFS), 최선 우선 탐색(Best First Search/Heuristic Search)이 있다. 그냥 뇌 없이 짤 수 있다는 것이 장점이다.

모든 경우의 수를 고려해야 하는 문제라면, DFS가 낫다. BFS 로도 구현이 물론 가능하지만, BFS로 구현했다간 큐의 크기가 말도 안되게 커진다. 그리고 DFS와 비교했을 때 심지어 속도도 똑같다. 따라서 경우의 수 구하기는 일반적으로 DFS가 편리하다. 대다수의 문제들은 DFS를 써도 일단 답은 나온다. (단, 시간복잡도에서의 불리함은 감수해야 한다)

(원하는 값이 없으면 원래의 값으로 돌아가 다른 값을 탐색)

4) 나의 알고리즘 사고의 단계

처음 파일을 봤을 때 SUBCLASS 와 비슷한 멘붕이 왔지만 미리 작성된 HTML 은 어떤식으로 구성돼있고, 각 JS 파일은 어떤 상호작용을 하는지 이해하니 문제에 한발짝 접근할 수 있었다.

우선 매 문제를 접근할 때 기본적인 나의 사고는 다음과 같다.

  1. 이 문제를 진행해야 하는 '목적' 이 무엇인가?
  2. 이 문제는 어떠한 것을 해결하기를 원하는가?
  3. 이 문제는 어떠한 형태로 구성되어 있는가?

5) N-QUEENS

우선 N-QUEENS 스프린트의 목적은 백트래킹의 개념을 익히기 위한 것이고, 백트래킹에서도 DFS 의 개념을 좀 더 심도있게 배우기 위한 목적이라고 할 수 있겠다.

BoardViewer.html 을 열어보면 다음과 같은 이미지가 보인다.

그리고 이 구조를 콘솔로 찍어보면 다음과 같이 나온다.

위를 통해 알 수 있는 사실은 다음과 같다.

1. Board 는 배열로 이루어져있다.

2. 각 배열은 총 n개의 요소를 가지고 있다. (n*n 체스판)

3. HTML 에서 말이 있는 자리에는 배열에서 1, 없는 자리에는 0 으로 이루어져있다.

1. Board.js

hasRowConflictAt

주어진 행(rowIndex)에 충돌하는 말이 있는지 확인합니다.

hasRowConflictAt: function (rowIndex) {

}

일단, 충돌나는 상황이 어떤 상황인지 먼저 정리해보자. 충돌나는 상황은 다음과 같다.

충돌 나는 상황 예시


0: (4) [0, 1, 0, 1] //  각 행에 1이 하나 이상 있을 경우
1: (4) [0, 0, 0, 1]
2: (4) [1, 0, 0, 0]
3: (4) [0, 0, 1, 0]

=>  TRUE (충돌이 있다!)

💡 나의 해결 방법


// 1. 입력받은 rowIndex 는 특정 행 (가로) 을 원하는 것이므로 변수에 해당 배열의 주소를 참조해 특정 배열에 접근할 수 있게 한다.


let row = this.attributes[rowIndex]


// 2. 1이 두 개 이면 false 를 리턴해야 하므로 `let num = 0` 이라는 변수를 만들어준다.


let num = 0;


// 3. 우리는 그 배열에 1이 두 개 있을 경우 즉, 그 합이 2 일 경우 TRUE 를 리턴할 것이므로 `num+= row[i]` 를 만들어줘서 요소 중 1이 있다면 num 에 그 합이 저장되게끔 한다.


for (let i = 0; i < row.length; i++) {
  num += row[i]
}

// 4. 그리고 조건문을 만들어줘서 num 이 1 이상이면 true 를 리턴하게 한다.

hasAnyRowConflicts

체스 판 위에 행 충돌이 하나라도 있는지 검사합니다.

충돌 나는 상황 예시


0: (4) [0, 1, 0, 0] 
1: (4) [0, 0, 0, 0]
2: (4) [1, 0, 0, 0]
3: (4) [0, 0, 1, 1] // 행 충돌이 하나라도 있는 경우 

=>  TRUE (충돌이 있다!)

💡 나의 해결 방법


// 1. 위에서 만든 함수를 통해 각 배열을 돌아 해당 함수를 통과하면 true 를 리턴하게 한다.

if (this.hasRowConflictAt(i)) {
  return true;
}

hasColConflictAt

주어진 열(colIndex)에 충돌하는 말이 있는지 확인합니다.

충돌 나는 상황 예시


0: (4) [0, 0, 0, 0] 
1: (4) [0, 0, 0, 0]
2: (4) [0, 0, 1, 0]
3: (4) [0, 0, 1, 0] // 각 열에 1이 하나 이상 있을 경우

=>  TRUE (충돌이 있다!)

💡 나의 해결 방법

// 1. hasRowConflictAt 과 패턴은 비슷한데 열의 요소에 접근해야 한다.
// 즉, 각 배열의 colIndex 값에 접근해야 하므로 반복문을 통해 다음과 같이 접근한다.

for (let i = 0; i < attr.n; i++) {
  num += attr[i][colIndex]
}

// 2. 그리고 num 이 1 이상이면 true 를 리턴하게 한다.

if (num > 1) {
  return true;
}

hasAnyColConflicts

체스 판 위에 열 충돌이 하나라도 있는지 검사합니다.

충돌 나는 상황 예시


0: (4) [1, 0, 0, 0] 
1: (4) [0, 0, 0, 1]
2: (4) [0, 0, 1, 0]
3: (4) [0, 0, 1, 0] // 열 충돌이 하나 이상 있을 경우

=>  TRUE (충돌이 있다!)

💡 나의 해결 방법

// 1. 위에서 만든 hasColConflictAt 함수를 이용해 각 배열을 돌아서 해당 함수를 통과하면 true 를 리턴하게 한다.

for (let i = 0; i < arr.length; i++) {
  if (this.hasColConflictAt(i)) {
     return true;
}

hasSlashConflictAt

주어진 슬래시 대각선(/)에 충돌하는 말이 있는지 확인합니다.

충돌 나는 상황 예시


0: (4) [0, 0, 1, 0] 
1: (4) [0, 1, 0, 0] // 대각선에 충돌이 있을 경우
2: (4) [0, 0, 0, 0]
3: (4) [0, 0, 0, 0] 

=>  TRUE (충돌이 있다!)

💡 나의 해결 방법

첫 번째로, 우선 충돌을 일으키는 모든 대각선의 경우를 구해봤다.

// 1
arr[0][1], arr[1][0]
// 2
arr[0][2], arr[1][1]
// 3
arr[0][3], arr[1][2]
// 4
arr[1][3], arr[2][2]
// 5
arr[2][3], arr[3][2]

만약 매개변수로 1을 입력받았다면 arr[0][1], arr[1][0] 을 따져야 한다.

arr[i][매개변수] 으로 생각해보면 i 가 1씩 증가할 수록 전달받은 파라미터는 1 씩 감소하는 형태이다.

만약 4번과 5번과 같은 경우 다음과 같이 생각해볼 수 있다.

충돌 나는 상황 예시


0: (4) [0, 0, 0, 0, 0] // 매개변수 4를 입력받으면 arr[0][4] 부터 검사하면 된다.
1: (4) [0, 0, 0, 1] // arr[1][3]
2: (4) [0, 0, 1, 0] // arr[2][2]
3: (4) [0, 0, 0, 0] 

=>  TRUE (충돌이 있다!)

따라서 코드는 다음과 같이 작성한다.


// 1. this.rows() 를 나타낼 변수 arr 선언

 let arr = this.rows();


// 2. 카운트 할 숫자를 담을 변수 num 선언

 let num = 0;


// 3. 반복문을 통해 arr[i][매개변수] 값이 1이라면 num++

if (arr[i][SlashColumnIndexAtFirstRow] === 1) {
   num ++;
}

// 4. 만약 num 이 1 이상이라면 true 를 리턴

if (num > 1)  {
  return true;
}

// 5. 한 번 반복할 때 마다 입력 받은 매개변수를 1씩 줄인다

SlashColumnIndexAtFirstRow--;

hasAnySlashConflicts

체스 판 위에 슬래시 대각선(/)에 충돌이 하나라도 있는지 검사합니다.

💡 나의 해결 방법

반복문을 돌려 hasSlashConflicts 함수를 만족하면 true 를 리턴하게 하면 되지만, 문제는 이전과 같이 반복문을 돌리면 반복하는 횟수가 검사하는 횟수에 도달하지 못한다.

따라서 다음과 같이 코드를 작성했다.


// 반복하는 횟수를 arr 길이의 2배로 늘려준다.

for (let i = 0; i < arr.length * 2; i++) {
  if (this.hasSlashConflictAt(i)) {
    return true;
  }
}

hasBackSlashConflictAt

주어진 역 슬래시 대각선()에 충돌하는 말이 있는지 확인합니다.

충돌 나는 상황 예시


0: (4) [1, 0, 0, 0] 
1: (4) [0, 1, 0, 0] // 역 대각선에 충돌이 있을 경우
2: (4) [0, 0, 0, 0]
3: (4) [0, 0, 0, 0] 

=>  TRUE (충돌이 있다!)

💡 나의 해결 방법

위에서 구현한 hasSlashConflictAt 함수와 별 다를게 없다.

위 예시에 따르면 역 슬래시는 arr[0][0], arr[1][1] 의 패턴을 띄고 있다.

즉, i 값이 증가할 수록 매개변수도 같이 증가하는 형태라고 할 수 있다.

따라서 코드는 다음과 같이 작성했다.


// hasSlashConflictAt 과 동일하지만 다음만 다르게 한다.

BackSlashColumnIndexAtFirstRow++;

hasAnyBackSlashConflicts

체스 판 위에 역 슬래시 대각선() 충돌이 하나라도 있는지 검사합니다.

충돌 나는 상황 예시


0: (4) [0, 0, 0, 0] 
1: (4) [0, 0, 0, 0] 
2: (4) [1, 0, 0, 0]
3: (4) [0, 1, 0, 0] // 역 대각선에 충돌이 있을 경우

=>  TRUE (충돌이 있다!)

💡 나의 해결 방법

위와 같은 충돌상황을 감지하기 위해서는 배열이 다음과 같이 구성되어야 한다.

충돌 나는 상황 예시


0: (4) [0, 0, 0, 0, 0, 0]  // arr[0][-2]
1: (4)    [0, 0, 0, 0, 0]  // arr[1][-1]
2: (4)       [1, 0, 0, 0]  // arr[2][0]
3: (4)       [0, 1, 0, 0]  // arr[3][1]

=>  TRUE (충돌이 있다!)

따라서 함수에 전달할 i의 값으로 음수를 줌으로써 충돌을 감지하게 해줬다.


for (let i = arr.length - 1; i > -arr.length; i--) {
  if (this.hasBackSlashConflictAt(i)) {
    return true;
  }
}

2. solvers.js

findNRooksSolution

  1. n이 주어졌을 때 n rooks 문제의 해답 한 개를 반환합니다.
  2. 반환 값은 체스 판을 나타내는 2차원 배열입니다.
해답 상황 예시


0: (4) [1, 0, 0, 0] // Rooks 가 충돌나지 않는 경우
1: (4) [0, 1, 0, 0]
2: (4) [0, 0, 1, 0]
3: (4) [0, 0, 0, 1]

💡 나의 해결 방법

rooks 는 각 행, 열에 1이 2개 이상 있을 경우 충돌이 일어난다.

따라서 위의 예시와 같이 arr[0][0], arr[1][1]... 의 방법을 통해 충돌을 피할 수 있는 솔루션을 내줬다.

//  1. 솔루션을 담을 배열 생성

let solution = [];

// 2. board 생성

let board = new Board({n});

// 3. board 불러올 변수 생성

let boardRows = board.rows();

// 4. 위에서 설명한 것 처럼 반복문 구성

  for(let i = 0; i < n; i++) {
    boardRows[i][i] = 1;
  }

// 5. 솔루션에 boardRows 담기

solution = boardRows;

countNRooksSolutions

  1. n이 주어졌을 때 n rooks 문제의 전체 해답 개수를 반환합니다.
  2. 반환 값은 정수입니다.
해답 상황 예시


0: (4) [1, 0, 0, 0] // Rooks 가 충돌나지 않는 경우
1: (4) [0, 1, 0, 0]
2: (4) [0, 0, 1, 0]
3: (4) [0, 0, 0, 1]

💡 나의 해결 방법

일단 문제를 해결하기 위해 다음의 사고 단계를 거쳤다.

  1. Rooks의 충돌을 감지할 수 있는 함수가 구현되어 있는가?

    • YES, Board.js 에 이미 hasAnyRooksConflicts 함수가 구현되어 있다.

  2. 탐색을 하는 순서는 어떻게 구성할 것인가?

    • 위 함수는 각 행, 혹은 열에 충돌이 있는 경우 True 를 리턴하는 함수다. 따라서 arr[0][0] 부터 시작해 1번 함수를 조건으로 걸어줘서 충돌이 없다면 arr[0][1] 순으로 탐색하고, arr[0][1] 에 충돌이 있다면 그 열과 행은 더 이상 탐색할 필요가 없으므로 arr[1][1] 로 넘어가게 로직을 짠다.
      (충돌이 있다면 밑으로, 없다면 옆으로 탐색)

  3. COUNT 는 어떻게 해줄 것인가?

    • 각 행과 열이 충돌이 없을 때 count 를 해줘야 한다. 그 말인 즉슨 arr[0][0] 부터 arr[3][3] 까지 모두 돌았을 때 충돌이 없는 경우다. 따라서 아래처럼 arr[i][매개변수] 에서 매개변수 === boardRows.length 이면 count 를 해주는 형식으로 로직을 짠다.
해답 상황 예시


0: (4) [1, 0, 0, 0] 0 // arr[0][4]
1: (4) [0, 1, 0, 0] 0 // arr[1][4]
2: (4) [0, 0, 1, 0] 0 // arr[2][4]
3: (4) [0, 0, 0, 1] 0 // arr[3][4]
function recursion(col){
    if(col === boardRows.length){ 
      solutionCount++
    }
    for(let i = 0; i < boardRows.length; i++){
      boardRows[i][col] = 1 // 먼저 해당 배열의 요소에 1 값을 준다.
      if(!board.hasAnyRooksConflicts()){ // 조건문을 통해 충돌이 없다면
            recursion(col + 1); // 재귀함수를 호출하고 파라미터에 1을 더한값을 넣어준다.
      }
      boardRows[i][col] = 0; // 충돌이 있다면 해당 1 값을 다시 0으로 바꾼다.
    }
  }
 recursion(0) // 파라미터로 0을 전달해서 0부터 [0][0] 부터 탐색할 수 있게 한다.

// 다음은 디버깅 결과의 일부분이다.

boardRows[0][0], count : 0 // 1번 콜스택 저장
boardRows[0][1], count : 0  
boardRows[1][1], count : 0 // 2번 콜스택 저장
boardRows[0][2], count : 0 
boardRows[1][2], count : 0
boardRows[2][2], count : 0 // 3번 콜스택 저장
boardRows[0][3], count : 0
boardRows[1][3], count : 0
boardRows[2][3], count : 0
boardRows[3][3], count : 0
boardRows[0][4], count : 1
boardRows[1][4], count : 1
boardRows[2][4], count : 1
boardRows[3][4], count : 1 // 반복문 모두 종료
boardRows[3][2], count : 1 // 3번 콜스택으로 돌아가서 i에 1이 더해진뒤 다시 탐색을 시작하는 모습 ([2][2] --> [3][2])
boardRows[0][3], count : 1 // ... 반복

충돌이 없다면 해당 인덱스의 자식의 자식을 계속해서 파고드는 전형적인 DFS 구조이다.

그리고 여기서 가장 중요한 것은 콜스택 개념이다. 해당 자식의 자식을 파고들다가 더 이상 탐색할 것이 없으면 (반복문 종료) 바로 이전 스택으로 다시 돌아가서 다른곳을 탐색한다. 이 개념을 머릿속에 그려야 이해하기 편하다.

(이중 for문 과 비슷하지만 단지 재귀 때문에 머리로 디버깅하기 좀 더 복잡할 뿐이다)

findNQueensSolution

  1. n이 주어졌을 때 n queens 문제의 해답 한 개를 반환합니다.
  2. 반환 값은 체스 판을 나타내는 2차원 배열입니다.

💡 나의 해결 방법

위와 비슷하지만 반환 값으로 체스 판을 나타내는 2차원 배열을 원한다.

밑에 코드들의 일부분과 더불어 각 코드들이 왜 존재하는지에 대한 주석을 달아놨으니 편하게 해석했으면 좋겠다.

  if (n === 2 || n === 3) { // Queens 는 체스판이 2*2, 3*3 인 경우 충돌할 수 없는 값이 존재하지 않는다. 따라서 위의 값을 입력 받으면 바로 배열을 리턴하도록 한다.
    return boardRows;
  }

    if(col === boardRows.length){
      solution = boardRows;
      return; // [0][4] 일 때 return 을 해줌 (함수 종료) 으로써 나머지 call stack (부모들) 이 실행
      // 안하게 되면 [0][4] 까지 간다음에 나머지 콜스택들이 실행됨
      // 재귀를 탈출하기 위한 조건
    }

    for(let i = 0; i < boardRows.length; i++){
      boardRows[i][col] = 1;
      if(!board.hasAnyQueenConflictsOn(i, col)){ // conflict 안나면 재귀
        recursion(col + 1);
      }
      if(solution !== undefined){ // 나머지 콜 스택은 여기서 걸림 모든 콜 스택을 브레이크 걸어줌으로써 나머지 작업을 아예 종료
        // 이거 안하면 [2][3] 에서 안 끝나고 [3][3] 으로 다시 갈거임 그리고 모든 콜스택이 계속 recursion 을 통해 실행되고 이후 모든것이 conflict 나기 때문에 79번 때문에 결국 모든 값이 0이 될거임
        return; // for 문을 탈출하기 위한 조건
      }
      boardRows[i][col] = 0;
    }

countNQueensSolutions

  1. n이 주어졌을 때 n queens 문제의 전체 해답 개수를 반환합니다.
  2. 반환 값은 정수입니다.

💡 나의 해결 방법

만약 위에서 Queens 의 충돌 경우와 DFS 에 대해 이해했다면 분명 count 또한 어렵지 않게 구현할 수 있을 것이다.

profile
nyongho
두 줄 소개
이전 포스트

TIL 2020-11-19 (재귀 함수 문제)

다음 포스트

TIL 2020-12-21 (비동기, Promise)

0개의 댓글