[PL] Language Syntax : F1VAE -> FVAE & First Class Function

parkheeddong·2023년 6월 5일

Compiler / Programming Language

목록 보기

26/32

💨 지난 내용 ..

F1VAE는 First Order Function을 지원하기 때문에 다음과 같은 특징을 지닌다.
✔ 함수는 각각 다른 메모리에 저장된다.
✔ 함수는 함수를 인수로 받거나, 리턴하지 못한다.
✔ 함수는 오직 함수 호출 표현식에서만 사용될 수 있다.

🔔 First Class (High Order) Function

✔ 함수와 변수를 똑같은 방식으로 다룬다.
✔ 함수는 value처럼 이용될 수 있으며, 인자처럼 이용될 수 있다.
✔ 함수는 다른 함수에 의해 리턴될 수 있다.

➡ Extension of VAE : FVAE

Functions and VAE (FVAE) 에 First Class 함수를 더해보자!!

1) Concrete Syntax

FVAE는 익명함수만을 지원한다. 즉, 이름을 가지지 않은 함수!

e.g. (fun x -> x + 1)

단, (let in 키워드로) 변수에 binding함으로써 함수에 이름을 짓게 된다.

e.g. let f = (fun x -> x + 1) in …

🌳 Function Application

함수형 프로그래밍에서는, 함수 호출 대신 Function Application이 사용된다. 즉 함수 호출과 동일한 의미이다.

Example)

"f가 인자 3으로 호출되었다" 대신 "f가 3에 적용되었다"고 한다.
let f = (fun x -> x - 1) in
f 3

"(f 2) 는 인자 3으로 호출되었다"가 아닌 "(f 2)는 3으로 적용되었다"고 한다.
let f = (fun x y -> x + y) in
(f 2) 3

2) Abstract Syntax

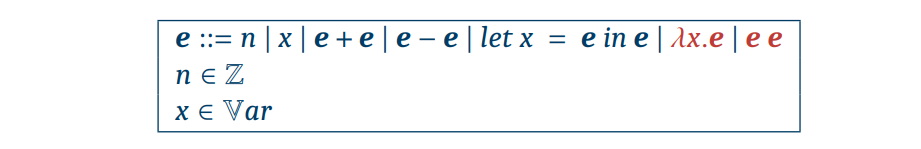
ʎx.e 와 e e가 추가된다.

Lambda Abstraction : ʎx.e
ʎx.e (x는 파라미터, e는 바디) 는 익명함수를 의미한다.
x는 binding occurence이고, x의 scope은 e다.

function application : e1 e2
e e 는 함수 호출(application)을 의미한다.
e1은 함수, e2는 인자이다.

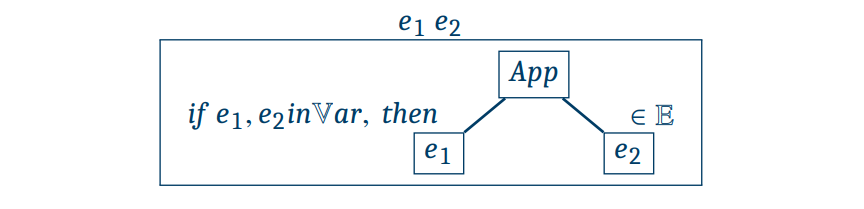
🌱 Abstract Syntax of FVAE in Ocaml

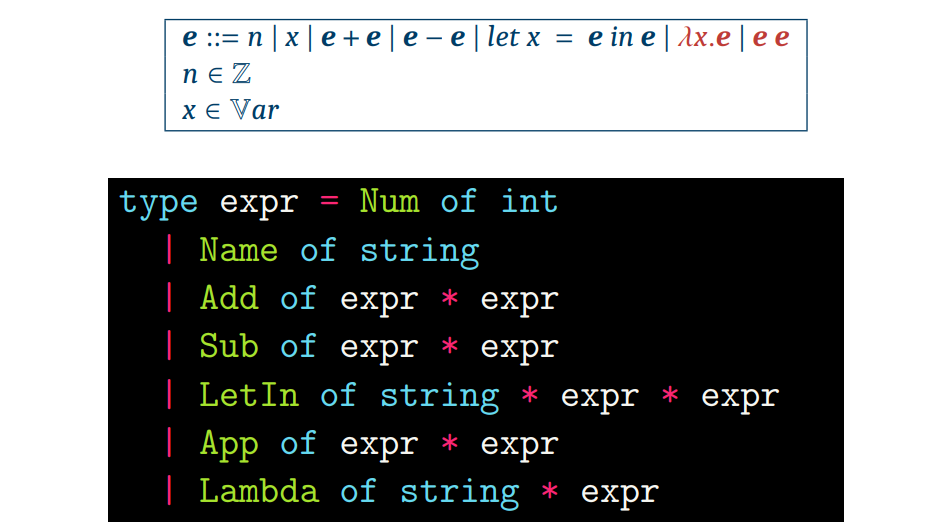
App of expr * expr
Lambda of string * expr

3) New Value Domain in FVAE

AE, VAE, F1VAE

Value = Integer(Z)

이전 AE, VAE, F1VAE에서는 ⭕Value는 오직 Integer(Z)⭕였다.

FVAE

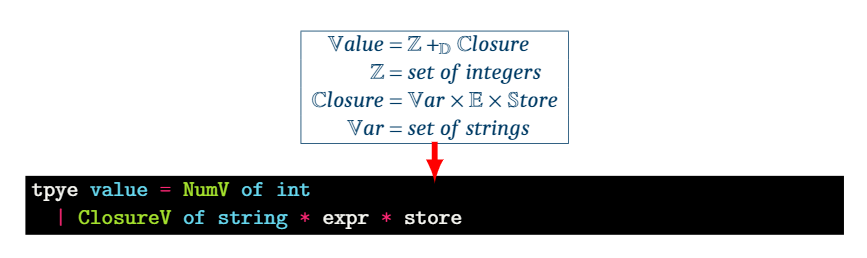
🌱 Value = Integer(Z) +D Closure

🌱 Closure = Var x E x Store

value의 범위가 함수까지 포용할 수 있도록 범위를 확장해야 한다.
FVAE에서 ⭕함수는 value일 수 있고, Closure⭕일 수 있다.

✔ Closure는 함수의 집합이다.

따라서 Var, expression, store을 포함한다. var는 파라미터, e는 함수 바디, store는 함수가 정의될 때의 abstract memory를 의미한다.

4) Domain Composition

기존에 존재하는 도메인들의 합으로서, 새로운 도메인을 정의해 보자!

C = A +D B

A와 B는 기존의 도메인이고, C는 새로운 도메인일 경우 다음과 같이 정의할 수 있다.

-> A +D B = A U B = { C | C ∈ A or C ∈ B }

❗❗ FVAE의 Value는 Integer(Z)와 Closure의 합집합이다.

Z +D Closure = Z U Closure { v | v ∈ Z or v ∈ Closure }

value의 원소는 'v'로 표시된다.
N : Integer(Z)의 원소.

🌱 <ʎx.e, σ> : Closure (Var x E x Store) 의 원소

🌱 Value Domain : in Ocaml

5) Abstract Memory for FVAE

VAE, F1VAE에서 Store는 Var -> Z 였다.
FVAE에서는 Store는 Var -> Value이다. (즉 integer 혹은 Closure을 반환)

따라서 새로운 Value domain을 다음과 같이 정의할 수 있다.

=> Ocaml의 "and" 키워드는 cross reference를 가능하게 한다. 즉 Type Store는 value를 참조할 수 있고, type value는 store을 참조할 수 있다.

6) Semantic Relations of FVAE

Semantics of E : ⇓E ⊆ Store × E × Value

∀σ∈Store. ∀e ∈E. ∀v∈ Value. σ⊢e ⇓E v ⇔ (σ, e,v) ∈⇓E

∀σ∈Store는 모든 추상 메모리(sigma)에 대해, ∀e ∈E는 모든 표현식(e)에 대해, ∀v∈ Value는 모든 값(v)에 대해, σ⊢e ⇓E v는 추상 메모리(sigma)에서 표현식(e)이 값(v)으로 계산된다는 것을 의미한다.

(FVAE 이전의 언어에서는 e는 정수 n으로 계산되었다)

⇔ (σ, e, v) ∈ ⇓E는 추상 메모리(sigma), 표현식(e), 값(v)의 쌍이 실행 동작(⇓E)을 통해 관련이 있다.

위의 표현식은 "모든 추상 메모리(sigma), 표현식(e), 값(v)에 대해, 추상 메모리(sigma)에서 표현식(e)이 값(v)으로 계산된다면 해당 쌍 (sigma, e, v)은 실행 동작(⇓E)에 속한다"는 의미이다.

❌ FVAE 언어에서는 Abstract Memory Fstore가 필요하지 않다.

우리는 F1VAE 함수 정보를 저장하기 위하여 Fstore을 만들었다. 그러나 FVAE에서는 함수가 변수처럼 취급되기 때문에, Seperate하게 Fstore을 이용할 필요가 없다.

❌ integer 도메인 Z도 필요 없다.

왜냐하면 Value에 integer 도메인이 포함되어 있기 때문이다.

7) Semantics of FVAE

FVAE언어를 위한 Semantic을 정의해 보자.

기존과 다른 점은 n이 아닌 v를 이용하고 있다는 점이다.

다른 언어들은 expression이 n으로 계산되었다면 FVAE에서는 v로 계산된다.

Rule Fun

ʎx.e는 Closure <ʎx, e, σ>로 계산된다.

📌 함수를 부르는 두가지 방법

1) Using Substitution = Rule App : e1 e2

σ 하에서, e1의 계산 결과가 <ʎx, e3, σ>이라면, 그리고 e2의 계산 결과가 v1이라면, 그리고 e3[v1/x]의 계산 결과가 v2라면, e1 e2는 v2로 계산된다.

2) Using Store = Rule App : e1 e2

σ 하에서, e1의 계산 결과가 <ʎx, e3, σ>이라면, 그리고 e2의 계산 결과가 v1이라면, 그리고 σ1[x↦v1] 하에서, 만약 e3의 계산 결과가 v2라면, e1 e2는 v2로 계산된다.