[SE] Program Verification

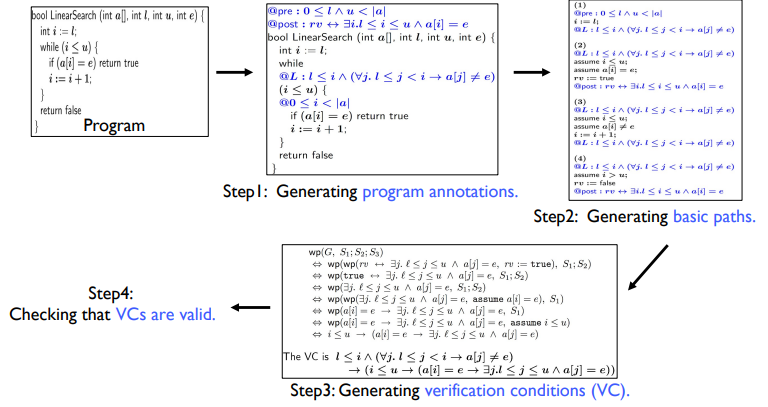
배열에서 l 과 u 사이에 내가 찾고자하는 값 e가 있는지를 체크하는 프로그램이다.

• formal parameter = array a, integer l, int u, int e

– ex) LinearSearch([1,3,5], 0, 2, 5) → true
– ex) LinearSearch([1,3,5], 0, 2, 2) → false

항상 이 이 프로그램이 잘 동작하는지 검증해보자.

1. 프로그램 검증

프로그램의 property를 명세하고, 검증하는 기술이다.

🌱 프로그램 명세 (program annotation)

First Order Logic을 이용하여 프로그램의 성질을 명세하는 것이다.

🌱 Partial Correctness Properties

어떠한 input이 주어지면 항상 기대하는 output이 나올 것이라는 것을 검증하는 것이다.

🌱 증명하기 위한 방법: verification methods

우리는 Inductive Assertion Method를 이용할 것이다.

2. First Order Logic (FOL)

FOL Is expressive enough to reason about programs.

implication이 False이기 위해선, F1 = True, F2 = False 여야 한다. 이 외는 True로 평가된다.
F1 -> F2 는 ~F1 U F2와 동일하다.

existential quantification
X*X = 4를 만족하는 X가 있다면, 위 식은 true이다.
universial quantification
모든 X에 대해서 X*X = 4를 만족한다면, 위 식은 true이다.

3. 프로그램 명세(anotation)의 3가지 종류

1) Function Specification

📌 precondition

함수를 시작하기 전에 항상 true가 되는 조건이다.
formal parameter을 이용해 precondition을 명세할 수 있다.

for (int x) {
	return √x)
}

이 경우 precondition은 x>=0 이다.

📌 postcondition

함수가 끝난 이후, 예상되는 output(리턴값)에 대한 조건이다.
formal parameter와 return value(rv)를 이용하여 명세할 수 있다.

for (int x) {
	return √x)
}

위 경우 postcondition은, return value가 √x일 것이다.

🔔 Example

배열에서 l 과 u 사이에 내가 찾고자하는 값 e가 있는지를 체크하는 프로그램이다.
✅ formal parameter= array a, integer l, int u, int e
ex) LinearSearch([1,3,5], 0, 2, 5) → true
ex) LinearSearch([1,3,5], 0, 2, 2) → false
✅ pre condition
0<= l ∩ u< |a|
(u는 a의 사이즈보다 작아야 한다)
✅ post condition
값 e가 array a 안에 있으면 true, 아니면 false 리턴
rv <-> ∃i (a[i] = e ∩ l<=i<=u)
∃∀∩

2) Loop Invariant

partial correctness를 증명하기 위해서, 각 loop은 loop invariant F로 annotate되어야 한다.

loop invariant는 loop을 시작하는 위치에 있다.

loop invariant F는 loop을 들어가기 전에는 항상 <condition>조건을 만족해야 하고, loop을 나갈 때에는 항상 ~<condition>만족해야 한다.

F ∩ <condition> holds on entering the body
F ∩ ~<condition> holds on exiting the loop

🔔 Example

loop invariant L = l <= i (∀j. l <= j < i -> a[j] != e)
i는 l보다 크거나 같아야 하고, l부터 i 사이 모든 j에 대해서(내가 여태까지 찾은 j에 대해서는) 모두 e가 아니어야 한다. 그래야 loop에 있을 수 있는 것이다.

3) Assertion

assertion은 loop invariant와 pre,post condition을 제외한 모든 formal comment로서, 프로그램의 임의의 위치에 있을 수 있다.

런타임에 생길 수 있는 문제가 될 수 있는 상황을 검증하고자 한다.

🔔 Example

index i에 있는 값이 e와 같은지 체크할 때, array out of bound를 체크하고 싶다면
if문 전에 0 <= i < |a|로 assertion을 작성할 수 있다.
혹은 나눗셈의 경우 division by zero 등의 문제를 assertion으로 작성할 수 있다.

4. Proving Partial Correctness

프로그램의 pre, post condition과 loop invariant, assertion을 통해 프로그램이 의도한 대로 작동하는지 확인하는 과정이다.

🌳 partial correctness

함수의 pre condition이 entry 지점에서 만족되고, 프로그램이 끝나고 나서 post condition이 늘 만족된다면 함수는 partially correct하다.
따라서 항상 pre, post condition이 만족되는 것으 증명하는 것!
이를 증명하기 위한 방법으로 'inductive assertion method'를 사용한다.

5. inductive assertion method

1) 함수로부터 verification conditions(VC) derive한다.

-> 요 부분을 배워볼 것 !

2) SMT Solver에게 VC의 Validity를 검증한다.

3) 만약 모든 VC가 유효하다면, 그 함수는 Partially correct하다.

🌳 verification condition을 만드는 과정

두가지 스텝으로 이뤄진다.

1) 함수를 basic path의 집합으로 나눈다.

2) 각 basic path마다 verification condition을 만든다.

❌ 문제 = loop과 recursive 함수는 path가 무한해질 수 있다는 문제가 있다.

그러나 정확한 loop invariant가 있다면, 유한한 basic path로 만들 수 있다. 재귀에 대해서도 function specification이 잘 정의되어 있다면 무한대로 늘어나는 것을 방지할 수 있다.

📌 Basic Path

함수의 precondition이나 loop invariant로 시작해서, loop invariant나 함수의 post condition으로 끝나도록 자를 수 있는 atomic statement의 sequence이다.

basic path는 다음과 같이 4가지로 나눌 수 있다.
pre -> loop invariant, loop invariant -> loop invariant, loop invariant -> post 이다.
loop invariant -> post는 loop에서 돌다가 조건문을 만족해서 post condition으로 갈 수도 있고, loop을 모두 다 끝내고 post condition으로 갈수도 있기 때문에 path가 2가지이다.

=> 이렇게 basic path 만드는 것 중요 !

📌 Weekest Precondition

{ precondition } ~ { post condition }

{ x > -1 } x:=x+1 { x > 0 }
{ y < 2.5 } y:=2*y { y < 5 }
{ x < 0 } x:=x+y { y > x }
{ True } assume a ≤ 5 { a ≤ 5 }
어떠한 조건을 쓰더라도 항상 만족한다. (조건이 없어도 만족한다)
{ b ≤ 5} assume a ≤ b{ a ≤ 5 }

weekest condition이란 pre condition 중에서 가장 general한, 범위가 넓은 것을 의미한다.

예를 들어 x := x+1이 x>0이기 위해서 pre condition이 x>-1이다. 그런데 x > 10이어도 post condition x>0 을 만족한다. 그러나 x>-1이 가장 general하기 때문에, 이것이 weekest pre condition이다.
따라서 위 5가지 예제는 모두 weekest condition이다!

📌 weekest precondition을 구하는 방법

weekest precondition transformer을 이용한다.

wp: FOL × stmts → FOL

1) assume statement에 대한 weekest precondition 구하기

wp(F, assume c) <=> c -> F
wp(a ≤ 5, assume a ≤ 5) ⇔ (a ≤ 5 → a ≤ 5) ⇔ True

2) assignment statement에 대한 weekest precondition 구하기

wp(F[v], v := e) ⇔ F[e]
wp(x > 0, x:=x+1) ⇔ (x+1 >0) ⇔ (x > -1)

3) statement개수가 여러개 있을 때

wp(F, S1; . . . ; Sn) ⇔ wp(wp(F, Sn), S1; . . . ; Sn-1)

맨 끝 statement부터 weekest precondition 구하고, sequentail하게 bakcward로 구하면 된다.

📌 verification condition 구하기

basic path의 verification condition은, pre condition -> weekest precondition 이다.

verification condition = F -> wp(G, S1; .. SN)
verification condition ={F} S1; ... SN {G}
위 두가지 방식으로 나타낼 수 있다.

Example 1

즉, 이것은 결국 (x>=0 -> x>=0)이므로 true이다.

Example 2

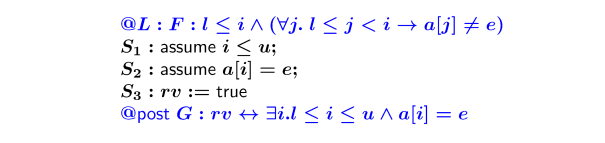
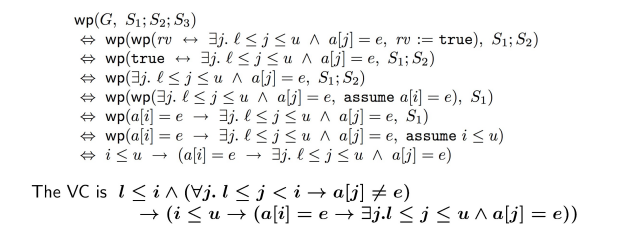
🌳 Partial Correctness

🌳 summary