🔔 Open Challenge
Dynamic Symbolic Execution의 해결하지 못한 두가지 난제를 알아보자.
1. Constraint Solving Cost
SMT Solver에 방정식을 주는데, 그 checking 과정에서 statisfiable 한지 판단하는 비용이 Constraint Solving Cost이다.
이 cost를 분석해 보니, 전체 테스팅 시간의 80%를 path condition을 푸는데 소모하고 있었다.
따라서 SMT Solver가 테스팅 시간의 대부분에 소요되고 있기 때문에 SMT Solver을 효과적으로 만드는 것이 중요한 과제다.
2. Path Explosion / State Explosion
프로그램의 탐험해야할 실행경로가 if/while statement 개수에 exponential하게 증가한다.
ex. grep 프로그램이 3836개의 분기문을 가지고 있다면 worst case에 탐험해야할 경로가 2의 3836승개이다.
이 문제를 어떻게 해결할 수 있을까?
✅ Example
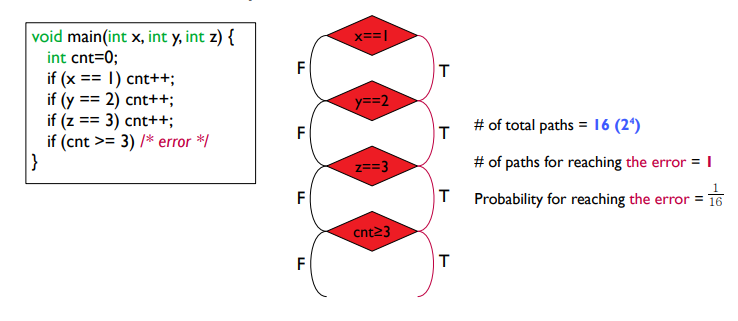
(1) 이 프로그램의 전체 실행경로는 2의 4승, 16개이다.
(2) 16개의 path 중에서 cnt >= 3, error 지점에 도달할 수 있는 path의 개수는 ?
-> 앞서 모든 브랜치에서 cnt++를 올려야 가능하기 때문에, (true,true,true,true) 로서 1개의 경로다.
(3) 따라서, Probability for reaching the error = 1/16이다.
✅ Example
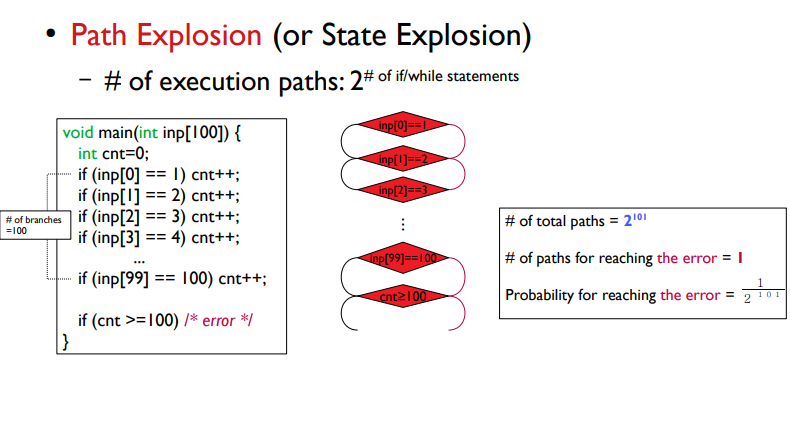
(1) # of total paths = 2 ** 101
(2) # of paths for reaching the error = 1
(3) probabililty of reaching the error = 1/ (2 ** 101)
-> 이렇게 path가 많은 경우, 랜덤하게는 해당 에러 지점에 도달하기 너무 어렵다. (확률이 매우 낮다)
🔔 Path Explosion의 솔루션
1) 어떤 경로부터 먼저 탐색할지 고민하고, 우선순위를 결정한다. = Search Heuristic
이미 수십만 path를 다 탐험할 수는 없으니, 어느 경로부터 실행해야 reward가 클지 (코드 커버리지를 밝힐 수 있는 방법이 무엇인지, 오류의 수를 최대로 찾아낼 수 있는지) 고민하는 것이다.
2) 탐험하지 않아도 되는 경로를 먼저 탐색한다. 즉 탐색할 필요가 없는 경로를 찾는다.
State Pruning heuristic (path-pruning heuristic)
해당 state를 도달하더라도 그로부터 만들어진 테스트 케이스는 코드 커버리지를 높이거나 오류를 찾아낼 수 없는 경우에, 해당 부분을 가지치기한다.
State Merging Heuristic (Path-merging heuristic)
기존 방법에서는 조건문에서 양쪽이 satisfiable한지 체크한다. state를 fork를 할 수 있음에도 불구하고 항상 state를 fork하지는 말고, 필요할 때에만 한다. 즉 경우의 수가 exponential하게 늘어나게 하지 말고, 선별적으로 하자.
🌳 Search Heuristic
coverage를 최대화하거나, 버그를 찾을 수 있는 branch를 선택하는 것이다.
쌓인 branch들 중 negate할 branch를 결정하는 권한을 가지는 것으로서, 그 기준을 결정하는 것이 search heuristic이다.
깊이우선 탐색을 하겠다면, 맨 마지막 브랜치를 뒤집을 것이다.
너비 우선 탐색을 하겠다면, 첫 브랜치를 뒤집을 것이다.
🌱 4가지 브랜치 선택 기준
1) CFDS(control-flow directed search)
현재 나의 실행 경로에서 "아직 도달해보지 못한 분기(브랜치) 중 가장 가까운 거리에 있는 분기"가 가장 도달하기 쉬울 것이다.
현재 path에서 도달해보지 못한 브랜치인 b4, b8중 b4가 b8보다는 더 빨리 도달하기 쉬울 것이다.
거리 계산 방법 = 아직 도달하는 브랜치와 현재 경로 사이의 거리
현재 path가 b1-b2-b3일때
distance(b1) - 이미 도달한 path뿐이다.
distance(b2->b8) - 4개
distance(b3->b4) - 1개
따라서, b2를 뒤집는다.
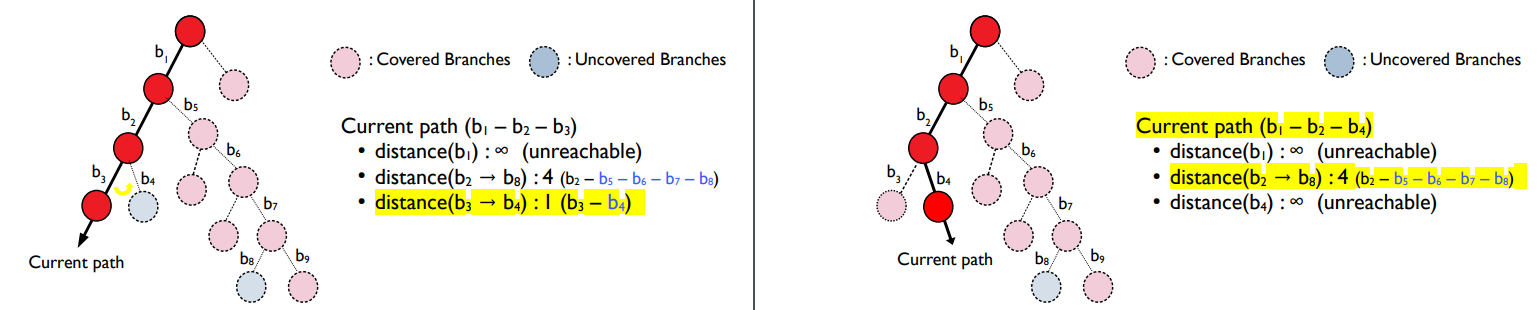
현재 path = b1- b2- b4
distance(b1) - unreachable
distance(b8) - 4개
distance(b4) - unreachable
따라서, 분기 b1를 뒤집는다.

현재 path = b1- b5- b6 -b7 - b9
distance(b1) - unreachable (뒤집어봤자 도달 불가)
distance(b5) - unreachable
distance(b6) - unreachable
distnace(b7) - unreachable
distance(b9) - 1 (b9 - b8)
따라서, 분기 b9를 뒤집는다.
이렇게 모든 브랜치를 커버할 수 있게 된다.
2) Generational Search
현재 path에서 가장 coverage gain이 높은 브랜치는 무엇인가?
step1. 경로에 있는 각 브랜치를 negate하고 실행한다.
step2. 각 선택된 브랜치의 coverage gain을 계산한다.
step3. 가장 높은 coverage gain을 가진 브랜치를 선택하여 뒤집는다.

현재 path = b1 - b2 - b3
gain(b1) = 2
gain(b2) = 4
gain(b3) = 1
coverage gain이 가장 큰 b2를 선택한다.
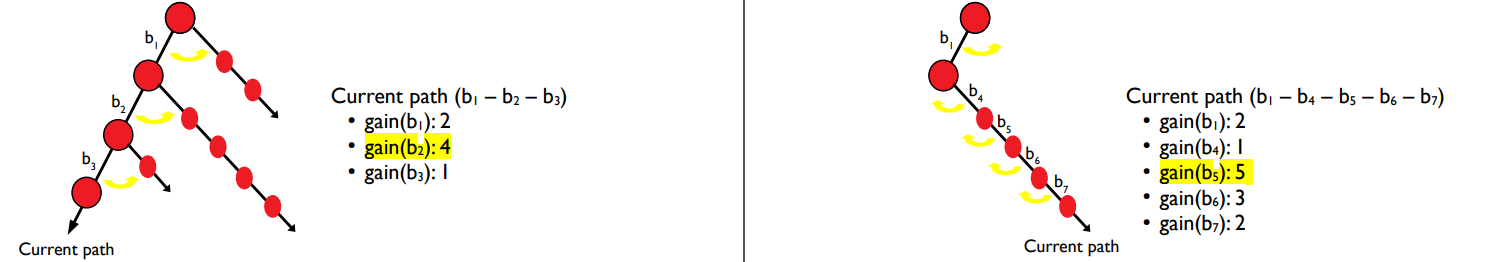
b2를 뒤집은 후, 현재 path = b1-b4-b5-b6-b7
gain(b1) = 2
gain(b4) = 1
gain(b5) = 5
gain(b6) = 3
gain(b7) = 2
-> b5를 뒤집는다.

이와 같이 계속하여 여덟개의 브랜치 중 coverage gain이 가장 높은 것을 선택하여 뒤집는다. 이를 반복 !
3) CGS
새로운 context를 가진 브랜치를 선택한다.
context = 현재 path에서 어떤 브랜치를 갔었는지에 대한 순서.

b1 - b4 - b6의 path였다면,
1-context of (b6) = b4이다. (depth 1)
2-context of (b6) = b4, b1이다. (depth 2)

1-context of b6이 b4일 떄, 위 두가지 케이스 중 path2가 더 새로운 context이다. depth 1만 고려헀을 때, b4는 가본 path이고 b3은 아니기 때문이다.
따라서 b3을 선택하면, 이제 1-context of b6 = b4, b3이 된다.