[PL] Syntax Analysis : Deterministic Parsing, First/Follow Function

1. Top-down Parsing의 문제

Top-down Parsing은 차례대로 production rule을 적용해 보면서 backtracking을 하게 된다. 그러나 backtracking은 시간이 많이 소요되기 때문에, 특정 제약 조건을 붙여서 '결정적인 구문 분석'을 할 수 있다.

➡️ 주어진 string과 같은 string을 생성하기 위해서, 현재의 입력 symbol를 보고 적용하면 되는 production rule을 결정적으로 선택함으로써 유도하는 것이다.

그리고 현재의 입력 symbol과 생성된 터미널의 symbol이 같지 않으면 주어진 string을 틀린 string으로 간주한다.

📌 Example

다음 문법에 대해 문자열 cabdd가 문법에 맞는 문장인지 Top-down Parsing으로 검사하고, 파스 트리를 구성해보자.

① S → cDd ② D → a ③ D → aE ④ E → bb ⑤ E → bd

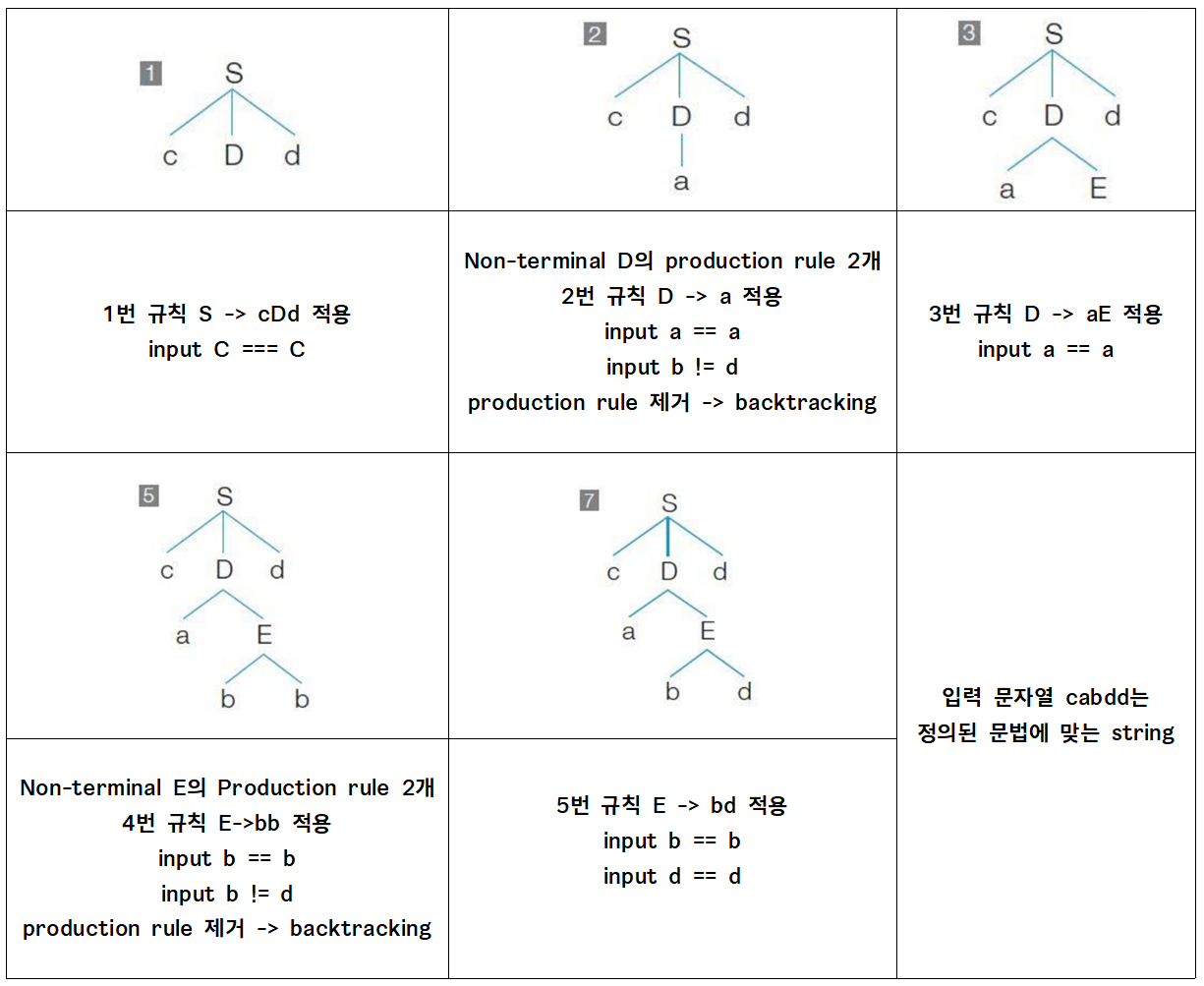
결정적 구문 분석을 위해서는 Non-terminal을 대체하는 production rule을 결정적으로 선택하기 위하여, Left-Factoring을 하고 First와 Follow를 사용한다.

2. Left-Factoring

Top-down Parsing에서 같은 Symbol을 Prefix로 갖는 두 개 이상의 Production Rule이 있을 때, 구문 분석기가 어떠한 생성 규칙을 적용해야 하는지 알 수 없다.

따라서 구문 분석 결정 과정에서 다음 Symbol을 볼 때까지 연기함으로써 혼란을 막고, Backtracking을 방지할 수 있다.

1) 정의

공통의 Prefix를 새로운 Non-terminal을 도입하여 인수 분해하는 것을 'left-factoring'이라고 한다.

📌 Example

A -> aB | aY // 공통의 a
<=> A -> a ( B | Y) // 인수분해
<=> A -> aA' // Left Factoring
A' -> B | Y

📌 Example

S -> ICTS | ICTSeS | a
C -> b

이 경우 공통 Prefix ICTS로 인수분해하여 S -> ICTS( $\epsilon$ | eS) 가 된다.

S -> ICTSS' | a
S' -> $\epsilon$ | eS
C -> b

3. Predictive Recursive Descent Parsers

1) Predictive Recursive Descent Parsers

Backtracking을 제거하는 효율적인 top-down parsing이다. 항상 그 다음 토큰만을 보고, backtracking을 하지 않기 때문이다.

Predictive recursive descent parser가 되기 위해서 우리는 다음과 같은 함수들을 정의해야 한다.

2) FIRST(a)

where a is a sequence of grammer symbols (non-terminal, terminals, and $\epsilon$). First(a) returns the set of terminals and $\epsilon$ that begin strings derived from a.
즉, 주어진 문법으로 생성될 수 있는 String의 첫 번째 글자를 리턴하는 함수이다.

✔️ Example

S -> A | B | C
A -> a // -> 만들어질 수 있는 string의 가능한 첫 번째 글자 = a
B -> Bb | b // b로 만들 수 있는 string = b, bb, bbb ...-> 만들어질 수 있는 string의 가능한 첫 번째 글자 = b
C -> Cc | 𝜺 // c로 만들 수 있는 string = 𝜺, c, cc, ccc... -> 만들어질 수 있는 string의 가능한 첫 번째 글자 = 𝜺 ,c
FIRST(S) =
FIRST(A) = { a }
FIRST(B) = { b }
FIRST(C) = { 𝜺 ,c }

📌 First Function의 Rules

아래 다섯가지 룰을 바탕으로 함수값을 계산한다.

1. FIRST( x ) = { x } if x is a terminal

2. FIRST( 𝜺 ) = { 𝜺 }

3. If A -> Bα is a production rule, then add FIRST(B) - { 𝜺 } to FIRST(A)

A -> Ba에 대해서, B의 First에 𝜺를 뺀 것을 A의 First에 추가한다.

4. If A -> B0B1B2…BiBi+1…Bk and 𝜺 ∈ FIRST(B0) and 𝜺 ∈ FIRST(B1) and 𝜺 ∈ FIRST(B2) and … and 𝜺 ∈ FIRST(Bi), then add FIRST(Bi+1) - { 𝜺 } to FIRST(A)

A -> B0B1..Bi+1..Bk 에 대해서, B0부터 Bi까지 𝜺 이 있으면 First(A)에 First(Bi+1) - 𝜺 을 넣어라.

5. If A -> B0B1B2…Bk and 𝜺 ∈ FIRST(B0) and 𝜺 ∈ FIRST(B1) and 𝜺 ∈ FIRST(B2) and … and 𝜺 ∈ FIRST(Bk), then add 𝜺 to FIRST(A)

A -> B0B1..Bi+1..Bk 에 대해서, B0부터 BK까지 𝜺 이 있으면 First(A)에 𝜺 을 넣어라.

✔️ Example

4번 룰 예시

S -> ABC
F(A) = { a, 𝜺 }
F(B) = { b, 𝜺 }
F(C) = { c }
인 경우,
만약 A와 B 모두 𝜺이 온다면 c가 A로 생성되는 문자열의 첫 글자가 될 수 있다.
즉 F(C) - { 𝜺 } 를 First(A)에 넣어라.

5번 룰 예시

S -> ABC
F(A) = { a, 𝜺 }
F(B) = { b, 𝜺 }
F(C) = { c, 𝜺 }
인 경우,
만약 A와 B, C 모두 𝜺이 온다면 S로 인해 생성되는 문자열이 𝜺 가 될 수 있기 때문에 𝜺 를 추가한다

✔️ Example

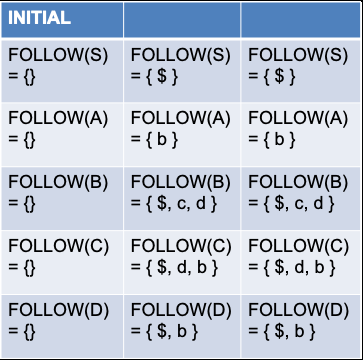
First(S), First(A), First(B), First(C), First(D) 구하기
S -> ABCD
A -> CD | aA
B -> b
C -> cC | 𝜺
D -> dD | 𝜺

4번 iteration까지 해 보면, 변화는 더 이상 생기지 않으므로 iteration을 멈춘다.

3) FOLLOW(A)

where A is a non-terminal. Follow(A) returns a set of terminals and $ (end of file) that can appear immediately after the non-terminal A.

✔️ Example

A -> aBb
B -> c|𝜺
이 context free grammer로 "ab"가 만들어질 수 있을까?!
A -> aBb -> a𝜺b -> ab로 가능하다.
사람은 B에서 c와 𝜺 중 𝜺를 골라야 한다는 것을 알지만, 컴파일러는 어떻게 알 수 있을까?!
컴파일러는 알지 못하기 때문에 Follow Function이 필요하다.
FOLLOW(B) = {b}이다.

📌 Follow Function의 Rules

아래 다섯가지 룰을 바탕으로 함수값을 계산한다.

1. If S is the starting symbol of the grammar, then add $ to FOLLOW(S)

$ 는 'EOF(End of File)'인데, end of string을 의미한다. S가 Starting Symbol이면 마지막으로 생성되는 문자열은 '전체 문자열'이 된다. 전체 문자열의 끝은 $이 된다.

2. If B → αA, then add FOLLOW(B) to FOLLOW(A)

B -> aA일 때, Non-terminal A가 가장 오른쪽 논터미널일 경우에 A의 다음에 나오는 String = B의 다음에 나오는 String이기 때문이다.

3. If B → αAC0C1C2…Ck and 𝜺 ∈ FIRST(C0) and 𝜺 ∈ FIRST(C1) and. 𝜺 ∈ FIRST(C2) and … and 𝜺 ∈ FIRST(Ck), then add FOLLOW(B) to FOLLOW(A)

4. If B → αAC0C1C2…Ck, then add FIRST(C0) – { 𝜺 } to FOLLOW(A)

A의 follow는 A 바로 뒤에 오는 것인데, A 뒤에 C0이 오고 있으므로 A의 follow는 C0의 first이다.
aAC0에서, Follow(A) == First(C0)이다.
따라서 Follow(A)에 First(C0) - {𝜺}를 추가한다.

5. If B → αAC0C1C2…CiCi+1…Ck and 𝜺 ∈ FIRST(C0) and 𝜺 ∈ FIRST(C1) and 𝜺 ∈FIRST(C2) and … and 𝜺 ∈ FIRST(Ci), then add FIRST(Ci+1) – { 𝜺 } to FOLLOW(A)

C0ㅂ터 Ci까지 입실론을 포함한다면 A 다음 바로 Ci+1이 올 수 있으므로, A의 Follow가 Ci+1의 First가 될 수 있으므로, First(Ci+1)-{𝜺}를 Follow(A)에 넣어준다.

✔️ Example

S -> ABCD
A -> CD | aA
B -> b
C -> cC | 𝜺
D -> dD | 𝜺

한 번 더 iteration을 해도 변화 없다!

4. Deterministic Top-down Parsing을 위한 두 가지 조건

Follow & First Function을 위해서는 Grammer가 2개의 condition을 만족해야 한다.

1) rule1.

A -> $\alpha$, A -> $\beta$인 경우 First($\alpha$) $\cap$ First($\beta$) = $\phi$ 이어야 한다.

✔️ why?

S -> Aa
A -> Aa | b
First(Aa) = {b}
First(b) = {b}
First(Aa)$\cap$ First(b) = {b} 이므로 문제
target string이 "b"인 경우, 컴파일러가 First로 판단할 때 두 가지 모두 b가 나오므로 어떤 것을 선택해야 할지 알 수 없다.

2) rule2.

$\epsilon$ $\in$ First(A), THEN First(A) $\cap$ Follow(A) = $\phi$ 이어야 한다.

✔️ why?

만약 교집합이 있을 경우 어떤 Production rule을 선택할지 컴파일러가 알지 못하므로 교집합이 공집합이어야 한다.
A -> B
B -> aB | 𝜺
target string = "a"
2개의 production rule이 있지만 둘 다 모두 'a'를 generate할 수 있다. 그 이유는 아래 때문 !
First(B) = { a, 𝜺 }
Follow(B) = { 𝜺 }

이 조건을 만족하지 못했다고 해서Ambiguous grammer인것은 아니지만 deterministic parsing을 할 수는 없다!

---

---

---

추가 예제1

다음 문법에서 각 논터미널 기호에 대한 FIRST를 구해보자
S → C | D
C → aC | b
D → cD | d

논터미널 기호는 S, C, D이므로 이것들에 대한 FIRST를 구하면 된다.
S ⇒ C ⇒ aC로 유도되므로 a는 S의 FIRST이다.
S ⇒ C ⇒ b로 유도되므로 b는 S의 FIRST이다.
S ⇒ D ⇒ cD로 유도되므로 c는 S의 FIRST이다.
S ⇒ D ⇒ d로 유도되므로 d는 S의 FIRST이다.
∴ FIRST(S) = {a, b, c, d}

C ⇒ aC로 유도되므로 a는 C의 FIRST이다.
C ⇒ b로 유도되므로 b는 C의 FIRST이다.
∴ FIRST(C) = {a, b}

D ⇒ cD로 유도되므로 c는 D의 FIRST이다.
D ⇒ d로 유도되므로 d는 D의 FIRST이다.
∴ FIRST(D) = {c, d}

추가예제 2

다음 문법에서 각 논터미널 기호에 대한 FIRST를 구해보자.
E → TE′
E′ → +TE′ | ε
T → FT′
T′ → *FT′ | ε
F → (E) | id

논터미널 기호는 E, E’, T, T’, F에 대한 FIRST를 구하면 된다.
E ⇒ TE′ ⇒ FT′E′ ⇒ (E)T′E′로 유도되므로 (는 E의 FIRST이다.
E ⇒ TE′ ⇒ FT′E′ ⇒ idT′E′로 유도되므로 id는 E의 FIRST이다.
∴ FIRST(E) = {(, id}

E′ ⇒ +TE′로 유도되므로 +는 E′의 FIRST이다.
E′ ⇒ ε으로 유도되므로 ε은 E′의 FIRST이다.
∴ FIRST(E′) = {+, ε}

⇒ FT′ ⇒ (E)T′로 유도되므로 (는 T의 FIRST이다.
T ⇒ FT′ ⇒ idT′로 유도되므로 id는 T의 FIRST이다.
∴ FIRST(T) = {(, id}

T′ ⇒ FT′로 유도되므로 는 T′의 FIRST이다.
T′ ⇒ ε으로 유도되므로 ε은 T′의 FIRST이다.
∴ FIRST(T′) = {*, ε}

F ⇒ (E)로 유도되므로 (는 F의 FIRST이다.
F ⇒ id로 유도되므로 id는 F의 FIRST이다.
∴ FIRST(F) = {(, id}