문제

• 링크 : https://school.programmers.co.kr/learn/courses/30/lessons/12921

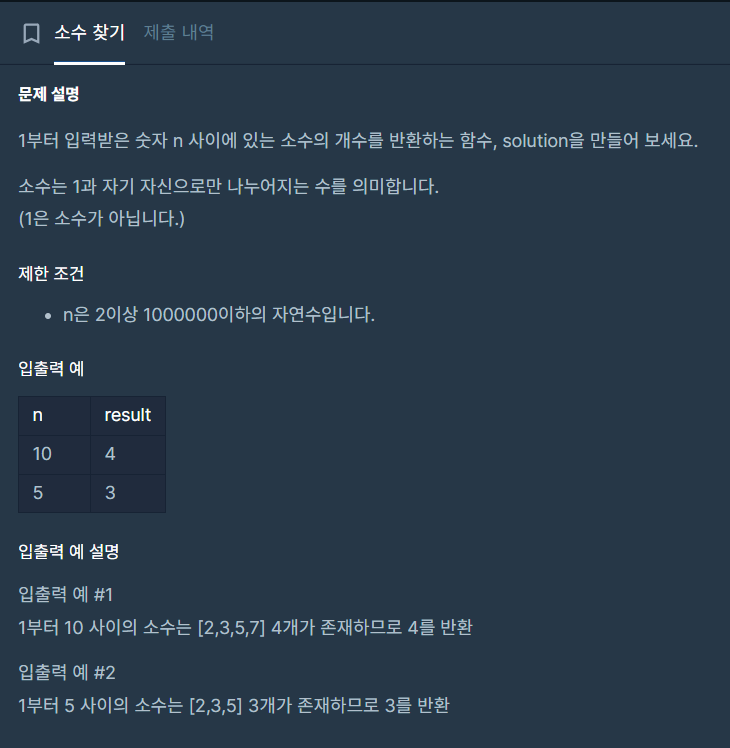
1부터 n이하의 수 중에서 소수의 개수를 return
소수 = 1과 자기 자신으로만 나누어지는 수 (1은 소수❌)

나의 풀이

• 첫번째 풀이 : 실패

접근 방법
while 조건문을 n보다 작거나 같을 때,
while문 안에서는 3부터 키워가면서 직접 나눔
나누어지면, false로 변경하고 break로 반복문 탈출
마지막에 +1은 무조건 2는 소수여서 3부터 시작했기 때문에 +1

class Solution {
    public int solution(int n) {
        
        int result = 0;
        boolean isPrime = true;
        int num = 3;
        
        while(num <= n) {
            for (int i = 2; i < num; i++) {
                if (num % i == 0) {
                    isPrime =  false;
                    break;
                }
            }
            num++;
            if(isPrime) {
                result++;
            }
            isPrime = true;
        }
        
        return result + 1;
        
    }
}

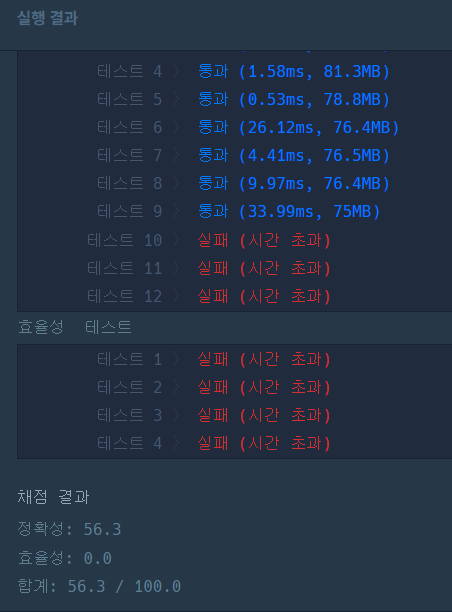
• 두번째 풀이 : 개념 공부 하고 성공

에라토스테네스의 체 ➡️ 소수 판별 알고리즘
소수가 되는 수의 배수를 지우면 남는 건 소수가 된다.

class Solution {
    public int solution(int n) {

        boolean[] isPrime = new boolean[n + 1];
        
        for (int i = 2; i < isPrime.length; i++) {
            isPrime[i] = true;
        }
        
        for (int i = 2; i * i <= n; i++) {
            if (isPrime[i]) {
                for (int j = i*i; j <= n; j +=i) {
                    isPrime[j] = false;
                }
            }
        }
        
        int result = 0;
        for (int i = 2; i < isPrime.length; i++) {
            if (isPrime[i]) {
                result++;
        }
    }
        return result;
    
    }
}

• 에라토스테네스의 체

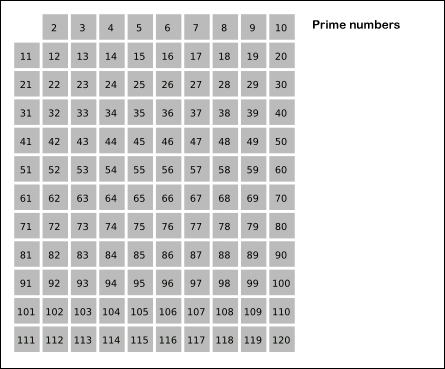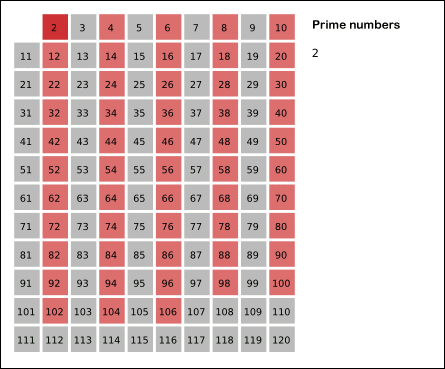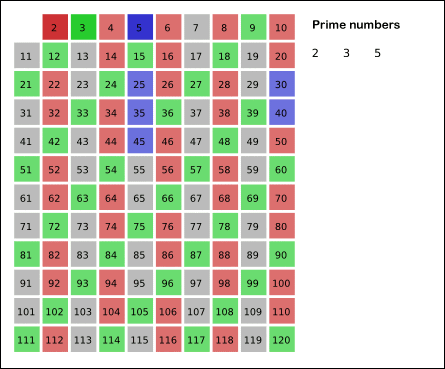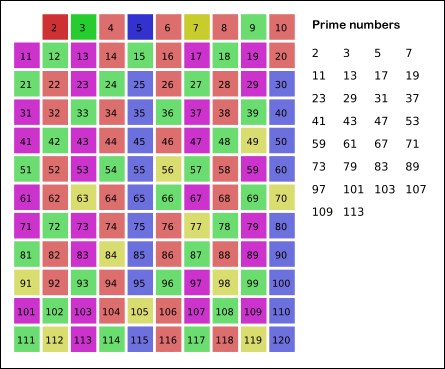
1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 
그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.

2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다. (보라색)

그림의 경우, 11^2 > 120 이므로 11보다 작은 수의 배수들만 지워도 충분하다. 
즉, 120보다 작거나 같은 수 가운데 
2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

https://colabear754.tistory.com/31